Storyboard

Im Falle von Boden kann angenommen werden, dass er mehrere Poren enthält, die kleine Kapillaren bilden, die ihn durchziehen. Auf dieser Grundlage können die Gleichungen für laminaren Fluss durch Röhren angewendet und die hydraulischen Widerstände von Kapillarnetzwerken berechnet werden. Diese Widerstände hängen von der Porosität ab und somit von dem Verhältnis der verschiedenen Bestandteile.

>Modell

ID:(370, 0)

Iframe

>Top

ID:(15203, 0)

Konzept

>Top

Die einzelnen Poren kommen zusammen und bilden Ketten, die Kapillaren erzeugen, durch die Wasser fließt.

Um dieses Phänomen zu modellieren, ist es notwendig, sowohl den Radius dieser Kapillaren als auch ihre Länge zu schätzen, wobei zu beachten ist, dass sie in der Regel nicht gerade verlaufen.

ID:(937, 0)

Konzept

>Top

ID:(2284, 0)

Konzept

>Top

Die Abschnitt Fluss ($S$) beinhaltet das von der Anzahl der Kapillaren ($N_p$) erzeugte die Porenabschnitt ($S_p$):

None

ID:(2285, 0)

Konzept

>Top

Wenn wir einen Querschnitt des Bodens betrachten, werden wir feststellen, dass die Kapillaren durch die Zwischenräume zwischen den Körnern verlaufen. Dadurch ist ihre Anzahl ähnlich der Anzahl der Körner selbst, sodass wir annehmen können, dass der Anzahl der Kapillaren ($N_p$) ähnlich der Anzahl der Körner in diesem Querschnitt ist:

None

ID:(2283, 0)

Konzept

>Top

ID:(2291, 0)

Konzept

>Top

Der Gesamtfluss wird als Summe der einzelnen Strömungen durch die verschiedenen Poren berechnet:

None

Wenn wir annehmen, dass alle Poren identisch sind, können wir der Gesamtfluss ($J_{Vt}$) erhalten, indem wir der Volumenstrom ($J_V$) einzeln mit der Anzahl der Kapillaren ($N_p$) multiplizieren.

ID:(2286, 0)

Gleichung

>Top, >Modell

Der Fluss von Flüssigkeit in einem porösen Medium wie Boden wird mithilfe der Variable die Flussdichte ($j_s$) gemessen, die die Durchschnittsgeschwindigkeit repräsentiert, mit der sich die Flüssigkeit durch das Medium bewegt. Bei der Modellierung des Bodens und wie die Flüssigkeit durch ihn hindurchfließt, stellt sich heraus, dass dieser Prozess von Faktoren wie die Porosität ($f$) und der Radius einer generischen Korns ($r_0$) beeinflusst wird, die, wenn sie größer sind, den Fluss erleichtern, während die Viskosität ($\eta$) den Durchgang durch Kapillaren behindert und die Fließgeschwindigkeit reduziert.

Das Modell integriert schließlich, was wir als die Hydraulische Leitfähigkeit ($K_s$) bezeichnen werden, eine Variable, die von den Wechselwirkungen zwischen der Radius einer generischen Korns ($r_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$) und die Generische eigene Porosität ($q_0$) abhängt:

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Bedingungen

Variablen

Beziehung

Entwicklung

Da die Flussdichte ($j_s$) durch die Gleichung:

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

mit der Radius einer generischen Korns ($r_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$), die Generische eigene Porosität ($q_0$), die Höhendifferenz ($\Delta h$) und der Probenlänge ($\Delta L$) in Beziehung steht, können wir einen Faktor definieren, den wir die Hydraulische Leitfähigkeit ($K_s$) nennen, wie folgt:

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Dieser Faktor umfasst alle Elemente, die mit den Eigenschaften des Bodens und der Flüssigkeit, die durch ihn fließt, zusammenhängen.

die Hydraulische Leitfähigkeit ($K_s$) drückt aus, wie leicht die Flüssigkeit durch das poröse Medium geleitet wird. Tatsächlich erhöht sich die Hydraulische Leitfähigkeit ($K_s$) mit die Porosität ($f$) und der Radius einer generischen Korns ($r_0$) und verringert sich mit die Generische eigene Porosität ($q_0$) und die Viskosität ($\eta$).

ID:(4739, 0)

Bild

>Top

Wenn wir die Literatur betrachten, finden wir Schätzungen der hydraulischen Leitfähigkeit für verschiedene Bodentexturen, die hier in Abhängigkeit von ihrem Exponenten dargestellt sind (d.h., -7 wird für eine hydraulische Leitfähigkeit von 1E-7 m/s angegeben):

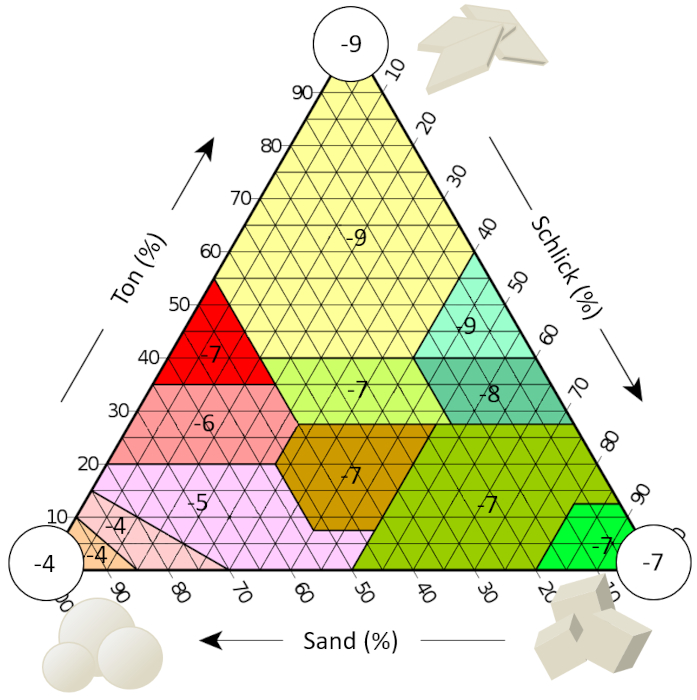
Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:

Diese Daten wurden aus der folgenden Literatur entnommen, die in der Spalte "hydraulische Leitfähigkeit" referenziert ist:

[1] "Geotechnical Engineering Principles and Practices" von Donald P. Coduto et al., Prentice Hall (1999)

[2] "Soil Mechanics and Foundations" von Muni Budhu, John Wiley & Sons. (2011)

[3] "Introduction to Environmental Engineering" von Mackenzie Davis und David Cornwell, McGraw Hill (2022)

[4] "Principles of Geotechnical Engineering" von Braja M. Das, CL-Engineering (2009)

[5] "Soil Mechanics in Engineering Practice" von Karl Terzaghi und Ralph B. Peck, John Wiley & Sons. (1996)

[6] "Soil Mechanics: Concepts and Applications" von William Powrie, CRC Press (2013)

ID:(4740, 0)

Top

>Top

Parameter

$\rho_w$

rho_w

Flüssigkeitsdichte

kg/m^3

$\pi$

pi

Pi

rad

$\eta_w$

eta_w

Wasser Viskosität

Pa s

Variablen

$S_t$

S_t

Abschnitt Boden

m^2

$S_1$

S_1

Abschnitt in Punkt 1

m^2

$S_2$

S_2

Abschnitt in Punkt 2

m^2

$S$

S

Abschnitt oder Bereich

m^2

$N_p$

N_p

Anzahl der Kapillaren

-

$\Delta p_2$

Dp_2

Druckdifferenz 2

Pa

$J_{Vt}$

J_Vt

Gesamtfluss

m^3/s

$J_V$

J_V

Hagen-Poiseuille Gesetz

m^3/s

$J_{Vt}$

J_Vt

Hagen-Poiseuille Gesetz für Boden

m^3/s

$\Delta h$

Dh

Höhe der Flüssigkeitssäule

m

$L$

L

Kapillarlänge

m

$S_p$

S_p

Porenabschnitt

m^2

$f$

f

Porosität

-

$R$

R

Porosität Funk

m

$J_{Vt}$

J_Vt

Probendurchfluss

m^3/s

Berechnungen

• Alternative Methode
• Traditionelle Methode
• Strategie
• 2D
• 3D

Gleichung

Zahl

Zuerst die Gleichung auswählen: zu , dann die Variable auswählen: zu

---

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable Gegeben Berechnen Ziel : Gleichung Zu verwenden

Gleichungen

ID:(15222, 0)

Gleichung

>Top, >Modell

Die Porosität ($f$) kann aus die Porenabschnitt ($S_p$) und die Abschnitt Fluss ($S$) mit folgender Formel berechnet werden:

$ f = \displaystyle\frac{ S_p }{ S }$

Bedingungen

Variablen

Beziehung

Entwicklung

Mit der Höhe die Infinitesimale Entfernung ($ds$) ist das Volumen von die Abschnitt Fluss ($S$)

$S ds$

und das der Poren mit die Porenabschnitt ($S_p$)

$S_p ds$

Daher wird die Porosität ($f$) wie folgt berechnet:

$f = \displaystyle\frac{S_p ds}{S ds} = \displaystyle\frac{S_p}{S}$

resultierend in folgender Gleichung:

$ f = \displaystyle\frac{ S_p }{ S }$

ID:(938, 0)

Gleichung

>Top, >Modell

Da der Querschnittsbereich eines Porenraums von Rohrradius ($R$) $\pi R^2$ beträgt und der Anzahl der Kapillaren ($N_p$) damit in Zusammenhang steht, können wir die Porenabschnitt ($S_p$) wie folgt berechnen:

$ S_p = N_p \pi R ^2$

Bedingungen

Variablen

$N_p$

Anzahl der Kapillaren

$-$

6039

$\pi$

Pi

3.1415927

$rad$

5057

$S_p$

Porenabschnitt

$m^2$

6040

$R$

Porosität Funk

$m$

6021

Beziehung

ID:(4362, 0)

Gleichung

>Top, >Modell

Mit die Porosität ($f$) und die Abschnitt Fluss ($S$) erhalten wir die Porenabschnitt ($S_p$), das geteilt durch den berechneten Kapillarquerschnitt von der Rohrradius ($R$) Der Anzahl der Kapillaren ($N_p$) ergibt, wie folgt:

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

Bedingungen

Variablen

$S_t$

Abschnitt Boden

$m^2$

6041

$N_p$

Anzahl der Kapillaren

$-$

6039

$\pi$

Pi

3.1415927

$rad$

5057

$f$

Porosität

$-$

5805

$R$

Porosität Funk

$m$

6021

Beziehung

Entwicklung

Wie die Porosität ($f$), berechnet mit die Porenabschnitt ($S_p$) und die Abschnitt Fluss ($S$) unter Verwendung von

$ f = \displaystyle\frac{ S_p }{ S }$

zusammen mit der Gleichung zur Berechnung von die Porenabschnitt ($S_p$) basierend auf der Anzahl der Kapillaren ($N_p$) und der Rohrradius ($R$) durch

$ S_p = N_p \pi R ^2$

ergibt sich

$f = \displaystyle\frac{N_p\pi R^2}{S}$

kann für der Anzahl der Kapillaren ($N_p$) gelöst werden und ergibt

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

ID:(4363, 0)

Gleichung

>Top, >Modell

Wenn wir davon ausgehen, dass die Anzahl der Kapillaren gleich der Anzahl der sichtbaren Körner in einem Querschnitt ist, können wir zeigen, dass für einen Kornradius von der Radius einer generischen Korns ($r_0$) und eine Porosität ($f$), der Rohrradius ($R$) gleich ist:

$ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

Bedingungen

Variablen

Beziehung

Entwicklung

Wenn wir den Bereich im Querschnitt betrachten, der keine Poren enthält, indem wir die Porenabschnitt ($S_p$) von die Abschnitt Fluss ($S$) subtrahieren und ihn durch den Bereich eines generischen Korns mit einem Radius von Radius einer generischen Korns ($r_0$) teilen, erhalten wir die Anzahl der sichtbaren Körner im Schnitt:

$\displaystyle\frac{S-S_p}{\pi r_0^2}=\displaystyle\frac{(1-f)S}{\pi r_0^2}$

wobei wir die Beziehung für die Porosität ($f$) verwenden:

$ f = \displaystyle\frac{ S_p }{ S }$

Wenn die Anzahl der Körner mit Anzahl der Kapillaren ($N_p$) gemäß dem Ausdruck ist:

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

wobei der Radius der Rohrradius ($R$) ist. Damit erhalten wir die Beziehung:

$\displaystyle\frac{(1-f)S}{\pi r_0^2}=\displaystyle\frac{fS}{\pi R^2}$

was zu folgendem Ergebnis führt:

$ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

ID:(109, 0)

Gleichung

>Top, >Modell

Wenn wir das Volumen eines Kapillars dem Volumen einer Kette von Körnern multipliziert mit der Probenlänge ($\Delta L$) gleichsetzen, erhalten wir eine Beziehung zwischen die Kapillarlänge ($l$) und die Porosität ($f$), die wie folgt lautet:

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

Bedingungen

Variablen

Beziehung

Entwicklung

Das Volumen des Kapillars kann aus der Rohrradius ($R$) und die Kapillarlänge ($l$) berechnet werden, was gleich dem Volumen einer Kette von Körnern von der Radius einer generischen Korns ($r_0$) und der Rohrlänge ($\Delta L$) multipliziert mit die Generische eigene Porosität ($q_0$) ist:

$\pi R^2 l = q_0 \pi r_0^2 \Delta L$

Dies in Verbindung mit die Porosität ($f$) in der Beziehung

$ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

ergibt die folgende Beziehung:

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

ID:(2215, 0)

Gleichung

>Top, >Modell

Der Gesamtfluss ($J_{Vt}$) wird berechnet, indem ein Anzahl der Kapillaren ($N_p$) mit dem Wert von der Volumenstrom ($J_V$) in jedem Kapillare multipliziert wird, wie folgt:

$ J_{Vt} = N_p J_V $

Bedingungen

Variablen

$N_p$

Anzahl der Kapillaren

$-$

6039

$J_{Vt}$

Gesamtfluss

$m^3/s$

6042

$J_V$

Hagen-Poiseuille Gesetz

$m^3/s$

6023

Beziehung

ID:(4364, 0)

Gleichung

>Top, >Modell

Wenn wir die Hagen-Poiseuille-Gleichung auf der Volumenstrom ($J_V$) für den Fall von Kapillaren mit der Rohrradius ($R$) in Bezug auf die Porosität ($f$) und die Kapillarlänge ($l$) als Funktion von der Probenlänge ($\Delta L$) anwenden, können wir der Gesamtfluss ($J_{Vt}$) berechnen, indem wir

verwenden. Das Ergebnis kann in Bezug auf die Abschnitt Fluss ($S$), die Viskosität ($\eta$), die Generische eigene Porosität ($q_0$), der Radius einer generischen Korns ($r_0$) und die Druckunterschied ($\Delta p$) ausgedrückt werden:

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Bedingungen

Variablen

$S_t$

Abschnitt Boden

$m^2$

6041

$\Delta p_2$

Druckdifferenz 2

$Pa$

5820

$J_{Vt}$

Hagen-Poiseuille Gesetz für Boden

$m^3/s$

6043

$L$

Kapillarlänge

$m$

6022

$f$

Porosität

$-$

5805

$R$

Porosität Funk

$m$

6021

$\eta_w$

Wasser Viskosität

$Pa s$

6020

Beziehung

Entwicklung

Um der Gesamtfluss ($J_{Vt}$) unter Verwendung von der Anzahl der Kapillaren ($N_p$) und der Volumenstrom ($J_V$) für jeden Kapillar durch

$ J_{Vt} = N_p J_V $

zu berechnen, erhalten wir der Anzahl der Kapillaren ($N_p$) mit die Porosität ($f$), die Abschnitt Fluss ($S$) und der Rohrradius ($R$) durch

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

und das Hagen-Poiseuille-Gesetz unter Verwendung von die Viskosität ($\eta$), die Druckunterschied ($\Delta p$) und die Kapillarlänge ($l$) wird berechnet mit

$J_v = - \displaystyle\frac{\pi R^4}{8\eta}\displaystyle\frac{\Delta p}{l}$

Unter Verwendung der Beziehung für der Rohrradius ($R$) in Bezug auf der Radius einer generischen Korns ($r_0$)

$ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

und für die Kapillarlänge ($l$), die Generische eigene Porosität ($q_0$) und der Probenlänge ($\Delta L$)

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

erhalten wir

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Diese Gleichung entspricht der Kozeny-Carman-Gleichung, die von Kozeny und Carman entwickelt wurde, um den Fluss einer Flüssigkeit durch ein poröses Medium zu modellieren, und wurde veröffentlicht in:

• Ueber kapillare Leitung des Wassers im Boden, J. Kozeny, Sitzungsber Akad. Wiss., Wien, 136(2a): 271-306 (1927)

• Flüssigkeitsfluss durch körnige Betten ("Fluid flow through granular beds"), P.C. Carman, Transactions, Institution of Chemical Engineers, London, 15: 150-166 (1937)

• Strömung von Gasen durch poröse Medien ("Flow of gases through porous media"), P.C. Carman, Butterworths, London (1956)

ID:(4365, 0)

Gleichung

>Top, >Modell

$ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$

Bedingungen

Variablen

$S_1$

Abschnitt in Punkt 1

$m^2$

5257

$S_2$

Abschnitt in Punkt 2

$m^2$

6017

$S$

Abschnitt oder Bereich

$m^2$

5405

Beziehung

Entwicklung

Mit Darcys Gesetz, wo die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) ist und der Gesamtfluss ($J_{Vt}$):

$ \Delta p = R_h J_V $

Daher ergibt sich mit der Gleichung für den Boden mit die Abschnitt Fluss ($S$), der Radius einer generischen Korns ($r_0$), die Viskosität ($\eta$), die Generische eigene Porosität ($q_0$), die Porosität ($f$), die Druckunterschied ($\Delta p$) und der Probenlänge ($\Delta L$):

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Deshalb ist die Hydraulic Resistance ($R_h$):

$ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$

ID:(10594, 0)

Gleichung

>Top, >Modell

In dem Fall eines Rohres, durch das eine Flüssigkeit mit die Wasserdichte ($\rho_w$) aufgrund von die Druckunterschied ($\Delta p$), verursacht durch eine eine Höhendifferenz ($\Delta h$) unter dem Einfluss der Schwerkraft, wie durch die Gravitationsbeschleunigung ($g$) dargestellt und mit folgender Gleichung berechnet, fließt:

kann dies in die Hagen-Poiseuille-Gleichung einbezogen werden, zusammen mit der Definition von die Flussdichte ($j_s$) in Bezug auf der Gesamtfluss ($J_{Vt}$), die wiederum von der Radius einer generischen Korns ($r_0$), die Generische eigene Porosität ($q_0$), die Porosität ($f$), die Viskosität ($\eta$) und der Probenlänge ($\Delta L$) abhängt:

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

Bedingungen

Variablen

$S_t$

Abschnitt Boden

$m^2$

6041

$\rho_w$

Flüssigkeitsdichte

$kg/m^3$

5407

$\Delta h$

Höhe der Flüssigkeitssäule

$m$

5819

$L$

Kapillarlänge

$m$

6022

$f$

Porosität

$-$

5805

$R$

Porosität Funk

$m$

6021

$J_{Vt}$

Probendurchfluss

$m^3/s$

6044

$\eta_w$

Wasser Viskosität

$Pa s$

6020

Beziehung

Entwicklung

Im Fall von Kapillaren, durch die eine Flüssigkeit mit die Flüssigkeitsdichte ($\rho_w$) aufgrund von die Druckunterschied ($\Delta p$), erzeugt durch eine Höhendifferenz ($\Delta h$) unter dem Einfluss der Schwerkraft, dargestellt durch die Gravitationsbeschleunigung ($g$), fließt und mit der folgenden Gleichung berechnet wird:

$ \Delta p = \rho_w g \Delta h $

kann dies in die Hagen-Poiseuille-Gleichung einbezogen werden, bezogen auf der Gesamtfluss ($J_{Vt}$), die wiederum von der Radius einer generischen Korns ($r_0$), die Generische eigene Porosität ($q_0$), die Porosität ($f$), die Viskosität ($\eta$), die Abschnitt oder Bereich ($S$) und der Probenlänge ($\Delta L$) abhängt, wie in der Gleichung beschrieben:

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Zusammen mit der Definition von die Flussdichte ($j_s$):

$j_s = \displaystyle\frac{J_{Vt}}{S}$

Erhalten wir:

$j_s=\displaystyle\frac{J_{Vt}}{S}=\displaystyle\frac{ r_0 ^2 }{8 q_g }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ L }$

resultierend in:

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

ID:(4366, 0)

Gleichung

>Top, >Modell

Um die hydraulische Leitfähigkeit mit den Massenfaktoren in Beziehung zu setzen, führen wir der Kapillarer Skalierungsfaktor ($\gamma$) zusammen mit der Radius einer generischen Korns ($r_0$), der Volumen eines Schlickkorns ($r_a$), die Generische eigene Porosität ($q_0$) und die Eigene Porosität des Sandes ($q_a$) als

$ \gamma = \displaystyle\frac{ r_0 ^2}{ r_a ^2}\displaystyle\frac{ q_a }{ q_0 }$

Bedingungen

Variablen

Beziehung

ein.

ID:(15101, 0)

Gleichung

>Top, >Modell

Aus der Definition von die Hydraulische Leitfähigkeit ($K_s$) und der Kapillarer Skalierungsfaktor ($\gamma$) können wir die Hydraulische Leitfähigkeit ($K_s$) in Bezug auf der Volumen eines Schlickkorns ($r_a$), die Eigene Porosität des Sandes ($q_a$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$) und die Viskosität ($\eta$) wie folgt ausdrücken:

$ K_s = \displaystyle\frac{ r_a ^2}{8 q_a }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta } \gamma $

Bedingungen

Variablen

Beziehung

.

ID:(977, 0)

Gleichung

>Top, >Modell

Die Berechnung von der Kapillarer Skalierungsfaktor ($\gamma$) ergibt sich aus die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$) und die Viskosität ($\eta$), unter Ausschluss von der Volumen eines Schlickkorns ($r_a$) und die Eigene Porosität des Sandes ($q_a$), durch die folgende Gleichung:

$\gamma=\displaystyle\frac{8K_sq_a}{r_a^2}\displaystyle\frac{(1-f)^2}{f^3}\displaystyle\frac{\eta}{\rho_wg}$

Wenn wir der Kapillarer Skalierungsfaktor ($\gamma$) mit die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$) in Beziehung setzen möchten, stellen wir fest, dass während sich ersterer um 6 Größenordnungen ändert, die letzteren nur um 2 Größenordnungen variieren. Daher macht es Sinn, eine Beziehung zum natürlichen Logarithmus von $\gamma$ herzustellen. Daher führen wir eine Regression mit der folgenden Gleichung durch:

$\ln \gamma = s_a g_a + s_i g_i + s_c g_c $

Bedingungen

Variablen

Beziehung

unter Verwendung von der Kapillarquerschnittsfaktor in Sand ($s_a$), der Kapillarquerschnittsfaktor im Schluff ($s_i$) und der Tonkapillarquerschnittsfaktor ($s_c$).

Die Mittelwerte für jede Spanne sind wie folgt:

Die Regression ergibt eine lineare Beziehung mit einem R-Quadrat-Wert von 0.9975 und den folgenden Koeffizienten, zusammen mit den Werten zur Beurteilung der Qualität der Koeffizienten:

Angesichts der p-Test-Werte können wir davon ausgehen, dass alle Koeffizienten von hoher Relevanz sind.

ID:(15100, 0)