Superposição de marés lunar-solar e efeito continente
Storyboard 
A sobreposição das marés lunares e solares leva a marés mais extremas ou a efeitos compensatórios que as reduzem. Além disso, há discussão sobre o efeito de que a água não pode se deslocar livremente devido à presença de continentes.
ID:(1577, 0)
Exemplo de marés
Imagem 
Se estudarmos os registros de marés em todo o mundo, observamos que:
• Existem duas marés por dia.
• Durante a lua cheia e a lua nova, as marés são maiores.
• Durante a lua crescente e minguante, as marés são menores.
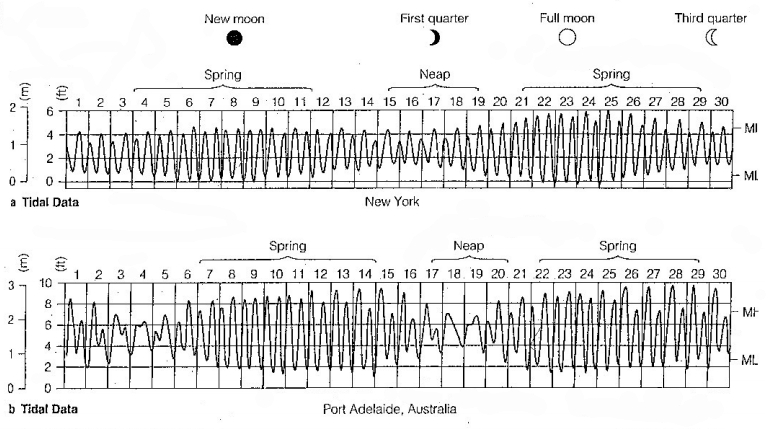
As marés "spring" e "neap" significam:
• Spring tide = maré de sizígia
• Neap tide = maré morta
ID:(11637, 0)
Marés mortas
Imagem 
Quando a lua está em um ângulo reto em relação à direção Terra-Sol, as marés são parcialmente neutralizadas. Isso ocorre sempre que há lua em quarto crescente ou quarto minguante.
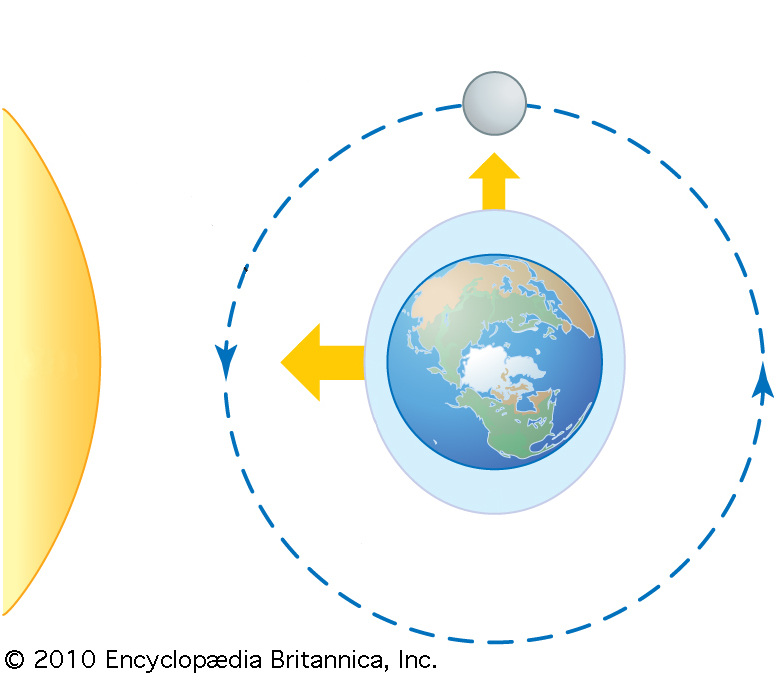
ID:(11642, 0)
Marés de primavera
Imagem 
Quando o sol e a lua se alinham, as marés se somam, criando uma maré mais alta. Isso ocorre sempre que há lua cheia (lua em oposição ao sol) ou lua nova (lua alinhada com o sol).
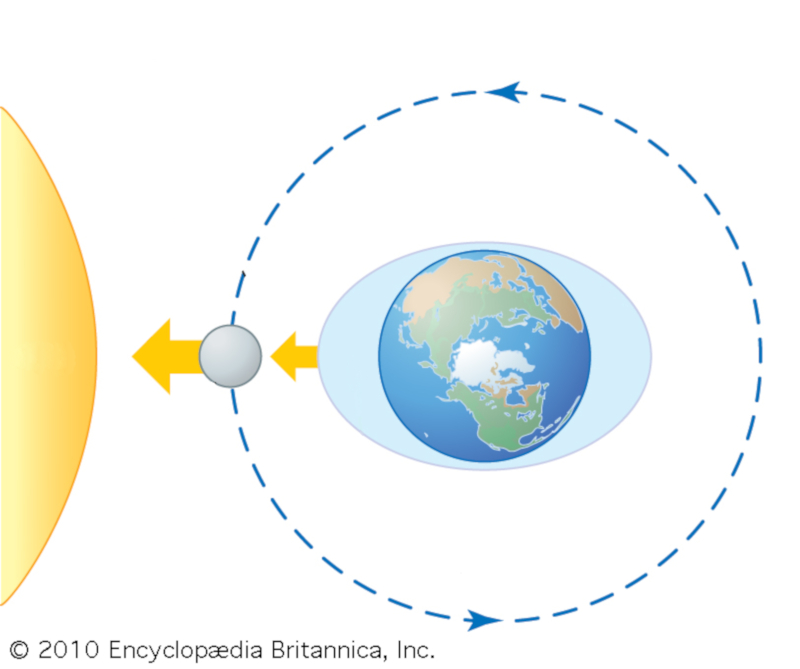
ID:(11641, 0)
Exemplo de marés extremas
Imagem 
Um exemplo extremo é ilustrado pela imagem de Alma, New Brunswick, Canadá, na Baía de Fundy. Essa maré excede em muito o valor máximo que ocorre quando o sol e a lua estão alinhados (24,42 cm + 53,5 cm = 77,92 cm). A razão para isso é o deslocamento da água, que é impedido pelo continente americano, levando a essa acumulação.

ID:(11660, 0)
Distribuição das alturas das marés no planeta
Imagem 
Se observarmos as medições das marés mais altas do planeta, podemos ver que:
• Elas ocorrem ao longo das costas devido ao acúmulo de água quando ela encontra obstáculos, como a linha costeira.
• Formam-se ondas que apresentam nós, pontos onde o nível do mar não varia.
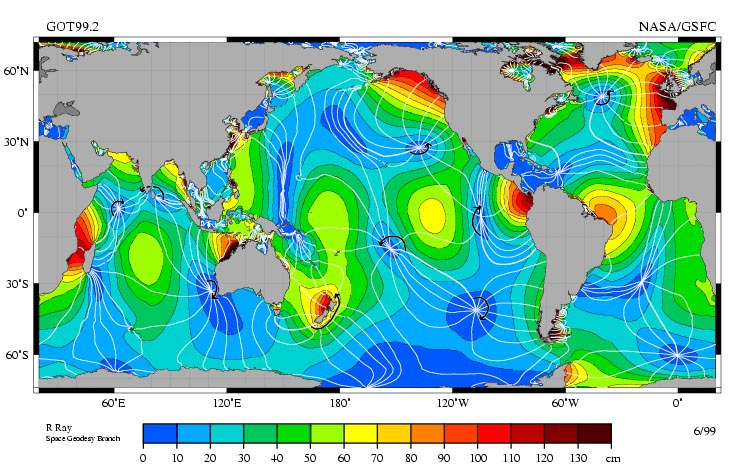
ID:(11638, 0)
Modelo
Top 
Parâmetros
Variáveis
Cálculos
Cálculos
Cálculos
Equações
h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
ID:(15438, 0)
Variação de profundidade na direção x (1)
Equação 
A mudança na aceleração implica que a coluna de água experimenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, isso é precisamente o que acontece. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
| g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R |
Com a variação no lado da conjunção com
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
e com
| \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right) |
Segue-se que a superfície se eleva com em
onde apenas a parte variável da variação foi considerada, uma vez que o termo GM/d^2 age sobre todo o sistema e não cria diferenças.
ID:(11653, 1)
Variação de profundidade na direção y (1)
Equação 
A mudança na aceleração implica que a coluna de água apresenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, é precisamente isso que ocorre. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
| g h_y = \Delta a_{cy} R |
Com a variação no lado da conjunção com
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
Como resultado, a superfície se eleva com em
ID:(11654, 1)
Variação de profundidade na direção x (2)
Equação 
A mudança na aceleração implica que a coluna de água experimenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, isso é precisamente o que acontece. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
| g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R |
Com a variação no lado da conjunção com
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
e com
| \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right) |
Segue-se que a superfície se eleva com em
onde apenas a parte variável da variação foi considerada, uma vez que o termo GM/d^2 age sobre todo o sistema e não cria diferenças.
ID:(11653, 2)
Variação de profundidade na direção y (2)
Equação 
A mudança na aceleração implica que a coluna de água apresenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, é precisamente isso que ocorre. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
| g h_y = \Delta a_{cy} R |
Com a variação no lado da conjunção com
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
Como resultado, a superfície se eleva com em
ID:(11654, 2)
