Superposición mareas lunares-solares y efecto continentes
Storyboard 
La superposición de las mareas lunares y solares resulta en mareas más extremas o en efectos de compensación que reducen las mareas. Además, se debate el efecto de que el agua no puede desplazarse libremente debido a la presencia de continentes.
ID:(1577, 0)
Ejemplo de mareas
Imagen 
Si uno examina los registros de mareas en todo el mundo, se observa que:
• Hay dos mareas al día.
• Durante la luna llena y la luna nueva, las mareas son más pronunciadas.
• Durante la luna creciente y menguante, las mareas son menos marcadas.
Las mareas "spring" y "neap" significan:
• Spring tide = marea viva
• Neap tide = marea muerta
ID:(11637, 0)
Mareas muertas
Imagen 
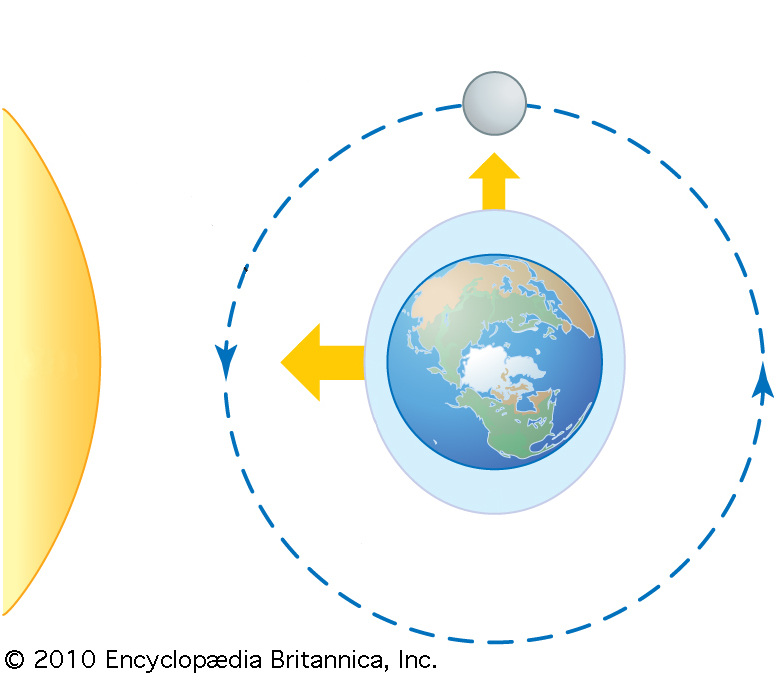
Cuando la luna se encuentra en un ángulo recto con respecto a la dirección tierra-sol, las mareas se contrarrestan parcialmente. Esto ocurre cada vez que hay luna en un cuarto creciente o menguante.
ID:(11642, 0)
Mareas vivas
Imagen 
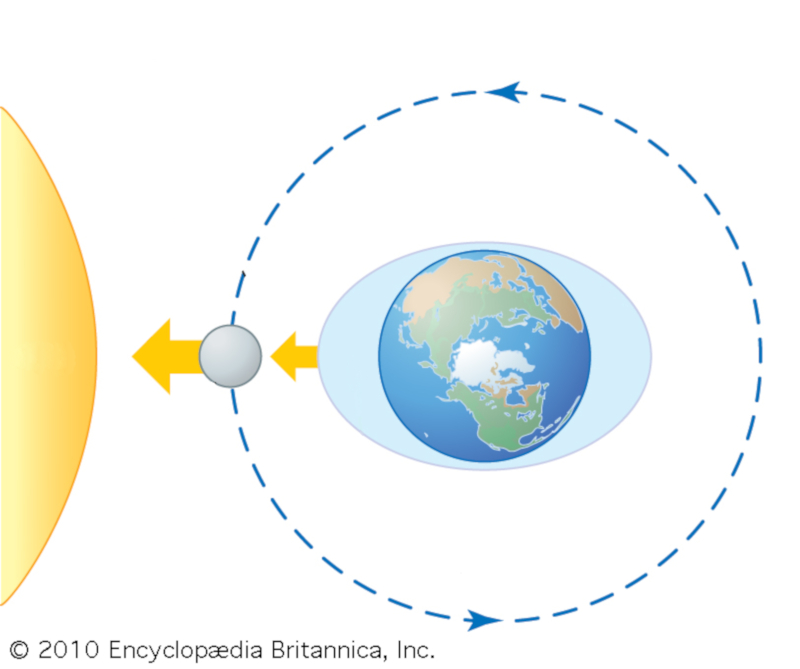
Cuando el sol y la luna están alineados, las mareas se suman, creando una marea más alta. Esto sucede cada vez que hay luna llena (la luna está en oposición al sol) o luna nueva (la luna está alineada con el sol).
ID:(11641, 0)
Ejemplo de mareas extremas
Imagen 
Un ejemplo extremo se observa en la siguiente imagen de Alma, New Brunswick, Canadá, en la Bahía de Fundy. Esta marea supera con creces el valor máximo que ocurre cuando el sol y la luna se alinean (24.42 cm + 53.5 cm = 77.92 cm). La razón es el desplazamiento del agua, que es detenido por el continente americano, lo que lleva a esta acumulación.

ID:(11660, 0)
Distribución de alturas de mareas sobre el planeta
Imagen 
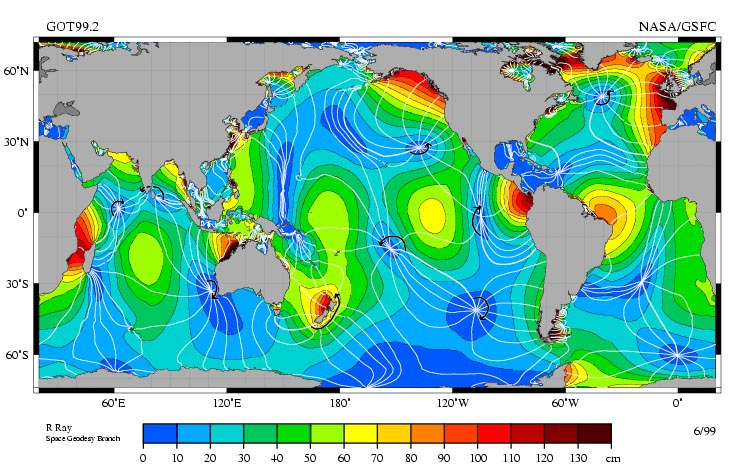
Si observamos las mediciones de las mareas más altas en el planeta, podemos notar que:
• Ocurren en las costas debido a que el agua se acumula cuando encuentra obstáculos como la línea costera.
• Se forman ondas que presentan nodos, puntos donde el nivel del mar no varía.
ID:(11638, 0)
Modelo
Top 
Parámetros
Variables
Cálculos
Cálculos
Cálculos
Ecuaciones
h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
ID:(15438, 0)
Variación de la profundidad en la dirección x (1)
Ecuación 
El cambio en la aceleración implica que la columna de agua experimenta una presión diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que ocurre. La modificación de la aceleración gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
| g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R |
Con la variación en el lado de la conjunción con
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
y con
| \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right) |
Se tiene que la superficie asciende con en
donde solo se tomó la parte que varía de la variación, ya que el término GM/d^2 actúa sobre todo el sistema y no crea diferencias.
ID:(11653, 1)
Variación de la profundidad en la dirección y (1)
Ecuación 
El cambio en la aceleración implica que la columna de agua experimenta una presión diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que ocurre. La modificación de la aceleración gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
| g h_y = \Delta a_{cy} R |
Con la variación en el lado de la conjunción con
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
Como resultado, la superficie se eleva con en
ID:(11654, 1)
Variación de la profundidad en la dirección x (2)
Ecuación 
El cambio en la aceleración implica que la columna de agua experimenta una presión diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que ocurre. La modificación de la aceleración gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
| g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R |
Con la variación en el lado de la conjunción con
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
y con
| \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right) |
Se tiene que la superficie asciende con en
donde solo se tomó la parte que varía de la variación, ya que el término GM/d^2 actúa sobre todo el sistema y no crea diferencias.
ID:(11653, 2)
Variación de la profundidad en la dirección y (2)
Ecuación 
El cambio en la aceleración implica que la columna de agua experimenta una presión diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que ocurre. La modificación de la aceleración gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
| g h_y = \Delta a_{cy} R |
Con la variación en el lado de la conjunción con
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
Como resultado, la superficie se eleva con en
ID:(11654, 2)
