Mond-Sonnen-Gezeitenüberlappung und Kontinenteneffekt
Storyboard 
Die Überlagerung von Gezeiten durch den Mond und die Sonne führt entweder zu extremeren Gezeiten oder zu kompensatorischen Effekten, die sie reduzieren. Darüber hinaus wird über den Effekt diskutiert, dass Wasser aufgrund der Anwesenheit von Kontinenten nicht frei fließen kann.
ID:(1577, 0)
Gezeitenbeispiel
Bild 
Wenn man die Gezeitenaufzeichnungen weltweit studiert, stellt man fest, dass:
• Es gibt zwei Gezeiten pro Tag.
• Während des Vollmonds und des Neumonds sind die Gezeiten höher.
• Während der zunehmenden und abnehmenden Mondsichel sind die Gezeiten niedriger.
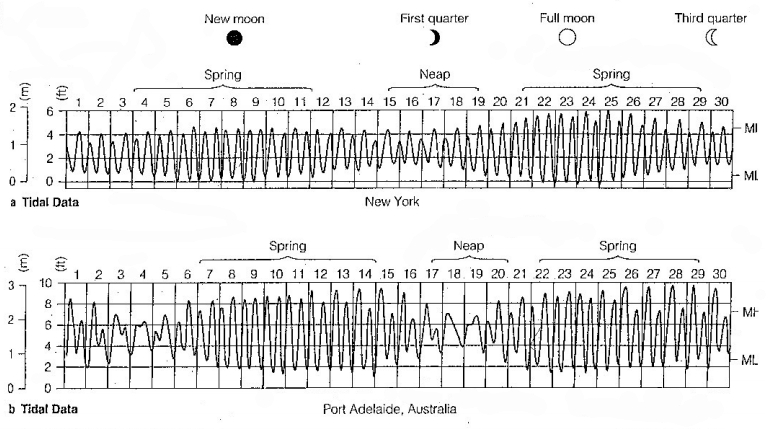
Die Begriffe "Springflut" und "Nipptide" bedeuten:
• Springflut = hohe Flut
• Nipptide = niedrige Flut
ID:(11637, 0)
Neaps Flut
Bild 
Wenn der Mond im rechten Winkel zur Richtung Erde-Sonne steht, werden die Gezeiten teilweise aufgehoben. Dies geschieht jedes Mal, wenn der Mond im ersten oder letzten Viertel steht.
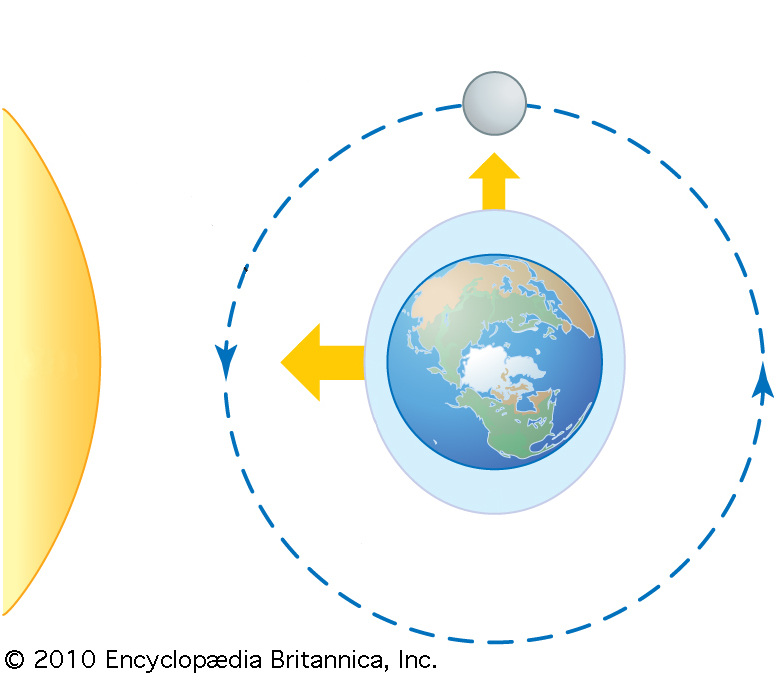
ID:(11642, 0)
Spring Flut
Bild 
Wenn sich Sonne und Mond ausrichten, vereinen sich die Gezeiten und erzeugen eine höhere Flut. Dies geschieht jedes Mal, wenn es Vollmond (Mond in Opposition zur Sonne) oder Neumond (Mond ausgerichtet mit der Sonne) gibt.
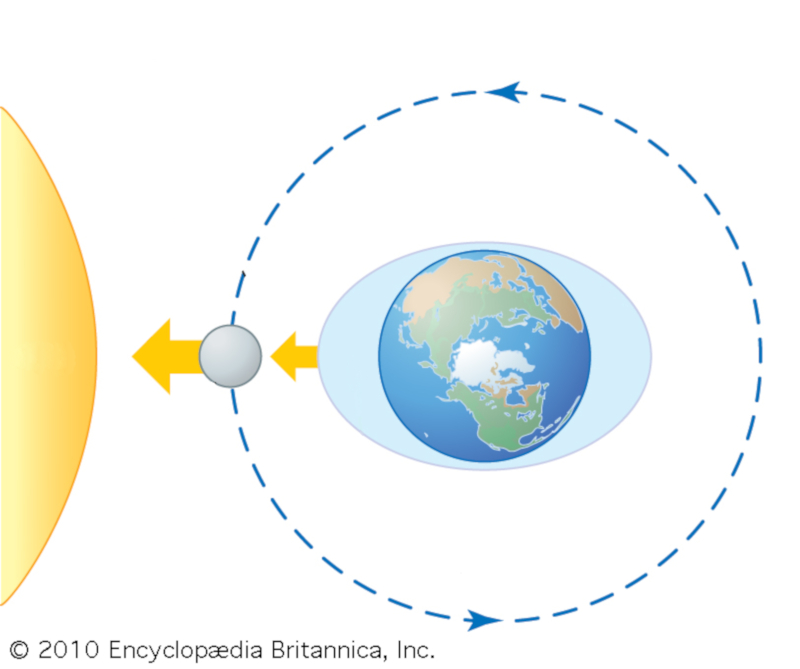
ID:(11641, 0)
Beispiel für extreme Gezeiten
Bild 
Ein extremes Beispiel zeigt das folgende Bild von Alma, New Brunswick, Kanada, in der Bay of Fundy. Diese Gezeiten übersteigen bei weitem den maximalen Wert, der auftritt, wenn Sonne und Mond sich ausrichten (24,42 cm + 53,5 cm = 77,92 cm). Der Grund dafür ist die Verschiebung von Wasser, das durch den nordamerikanischen Kontinent gestoppt wird und zu dieser Ansammlung führt.

ID:(11660, 0)
Verteilung der Gezeitenhöhen auf dem Planeten
Bild 
Wenn wir die Messungen der höchsten Gezeiten auf dem Planeten betrachten, können wir feststellen, dass:
• Sie entlang der Küsten auftreten, weil sich Wasser ansammelt, wenn es auf Hindernisse wie die Küstenlinie trifft.
• Wellen entstehen, die Knoten aufweisen, Punkte, an denen sich der Meeresspiegel nicht ändert.
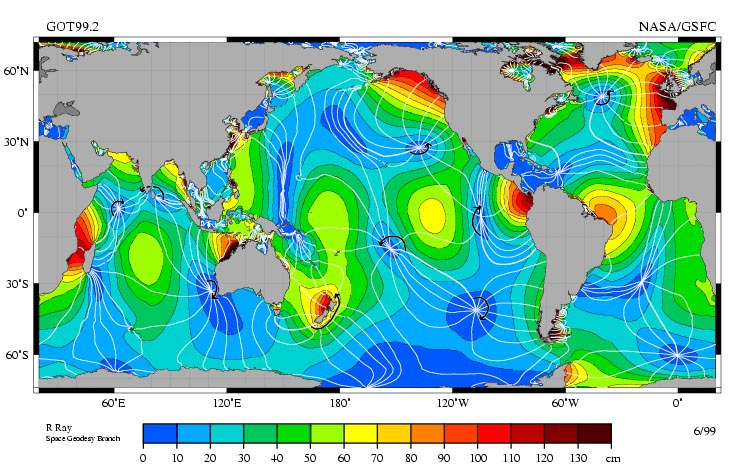
ID:(11638, 0)
Modell
Top 
Parameter
Variablen
Berechnungen
Berechnungen
Berechnungen
Gleichungen
h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
ID:(15438, 0)
Tiefenvariation in x-Richtung (1)
Gleichung 
Die Änderung in der Beschleunigung bedeutet, dass die Wassersäule eine unterschiedliche Druck erfährt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, geschieht genau das. Die Änderung der Gravitationsbeschleunigung wird durch eine Änderung in der Tiefe kompensiert, die der Gezeiten entspricht:
| g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R |
Mit der Variation auf der Konjunktionseite mit
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
und mit
| \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right) |
Es ergibt sich, dass die Oberfläche mit ansteigt in
wobei nur der variable Teil der Variation berücksichtigt wurde, da der Term GM/d^2 auf das gesamte System wirkt und keine Unterschiede erzeugt.
ID:(11653, 1)
Tiefenvariation in y-Richtung (1)
Gleichung 
Die Änderung der Beschleunigung bedeutet, dass die Wassersäule einen anderen Druck erfährt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, ist genau das der Fall. Die Modifikation der Gravitationsbeschleunigung wird durch eine Änderung der Tiefe ausgeglichen, die der Gezeiten entspricht:
| g h_y = \Delta a_{cy} R |
Mit der Variation auf der Seite der Konjunktion mit
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
Daraus ergibt sich, dass die Oberfläche mit ansteigt bei
ID:(11654, 1)
Tiefenvariation in x-Richtung (2)
Gleichung 
Die Änderung in der Beschleunigung bedeutet, dass die Wassersäule eine unterschiedliche Druck erfährt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, geschieht genau das. Die Änderung der Gravitationsbeschleunigung wird durch eine Änderung in der Tiefe kompensiert, die der Gezeiten entspricht:
| g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R |
Mit der Variation auf der Konjunktionseite mit
| \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right) |
und mit
| \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right) |
Es ergibt sich, dass die Oberfläche mit ansteigt in
wobei nur der variable Teil der Variation berücksichtigt wurde, da der Term GM/d^2 auf das gesamte System wirkt und keine Unterschiede erzeugt.
ID:(11653, 2)
Tiefenvariation in y-Richtung (2)
Gleichung 
Die Änderung der Beschleunigung bedeutet, dass die Wassersäule einen anderen Druck erfährt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, ist genau das der Fall. Die Modifikation der Gravitationsbeschleunigung wird durch eine Änderung der Tiefe ausgeglichen, die der Gezeiten entspricht:
| g h_y = \Delta a_{cy} R |
Mit der Variation auf der Seite der Konjunktion mit
| \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d } |
Daraus ergibt sich, dass die Oberfläche mit ansteigt bei
ID:(11654, 2)
