Superposition de marée lunaire-solaire et effet continent
Storyboard 
La superposition des marées lunaires et solaires entraîne des marées plus extrêmes ou des effets compensatoires qui les réduisent. De plus, il est discuté de l'effet selon lequel l'eau ne peut pas se déplacer librement en raison de la présence de continents.
ID:(1577, 0)
Exemple de marées
Image 
Si l'on étudie les relevés des marées à travers le monde, on observe que :
• Il y a deux marées par jour.
• Pendant les pleines lunes et les nouvelles lunes, les marées sont plus importantes.
• Pendant les premiers et derniers quartiers de lune, les marées sont moins importantes.
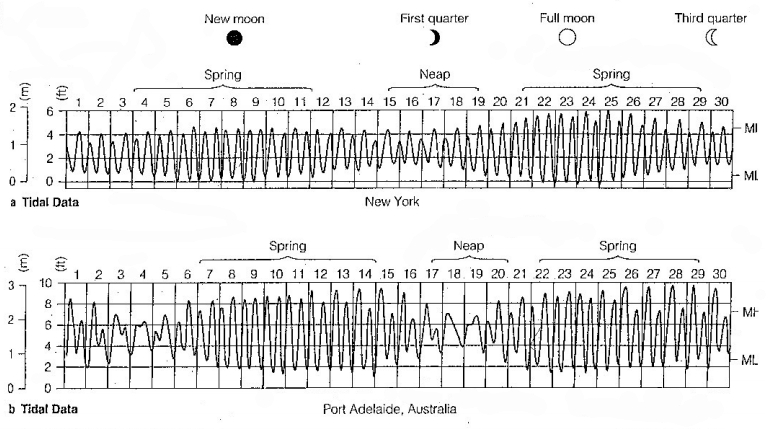
Les marées "spring" et "neap" signifient :
• Spring tide = marée de vive-eau
• Neap tide = marée de morte-eau
ID:(11637, 0)
Marées mortes
Image 
Lorsque la lune se trouve à un angle droit par rapport à la direction Terre-Soleil, les marées sont partiellement annulées. Cela se produit à chaque fois qu'il y a une lune en premier quartier ou en dernier quartier.
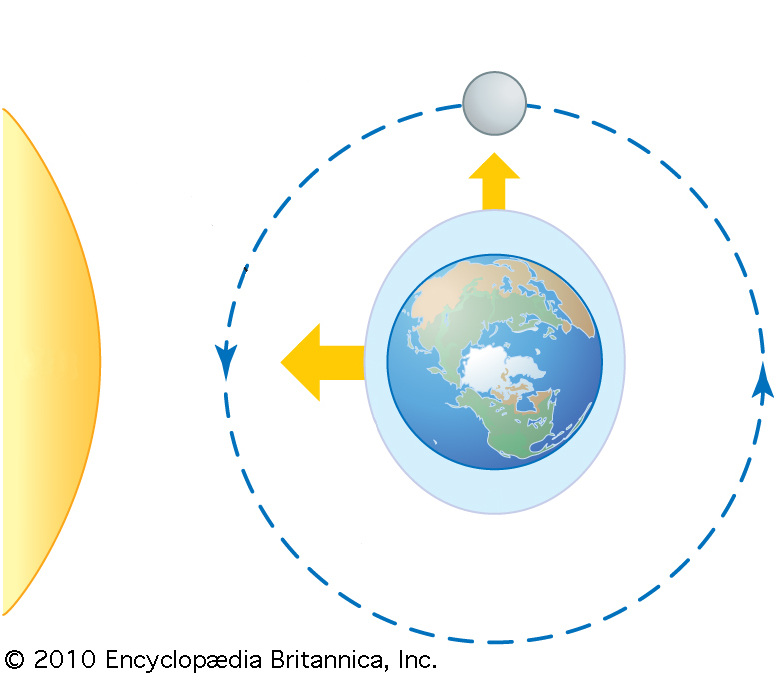
ID:(11642, 0)
Marées de printemps
Image 
Lorsque le soleil et la lune s'alignent, les marées s'additionnent, créant une marée plus haute. Cela se produit chaque fois qu'il y a une pleine lune (lune en opposition au soleil) ou une nouvelle lune (lune alignée avec le soleil).
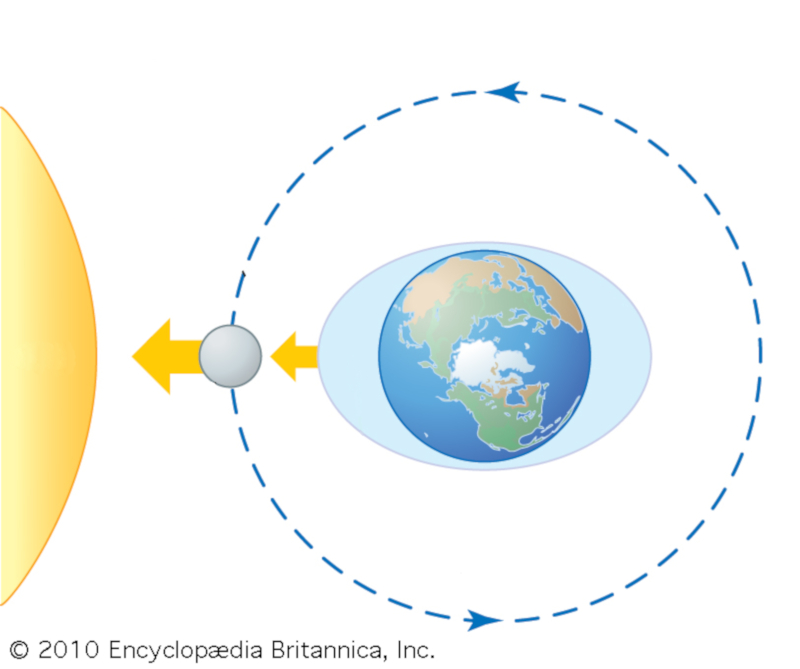
ID:(11641, 0)
Exemple de marées extrêmes
Image 
Un exemple extrême est illustré par l'image d'Alma, au Nouveau-Brunswick, au Canada, dans la baie de Fundy. Cette marée dépasse largement la valeur maximale qui se produit lorsque le soleil et la lune sont alignés (24,42 cm + 53,5 cm = 77,92 cm). La raison en est le déplacement de l'eau, qui est stoppé par le continent américain, conduisant à cette accumulation.

ID:(11660, 0)
Répartition des hauteurs de marée sur la planète
Image 
Si l'on observe les mesures des marées les plus élevées sur la planète, on peut constater que :
• Elles se produisent le long des côtes en raison de l'accumulation d'eau lorsque celle-ci rencontre des obstacles, comme la ligne côtière.
• Des vagues se forment, présentant des nuds, des points où le niveau de la mer ne varie pas.
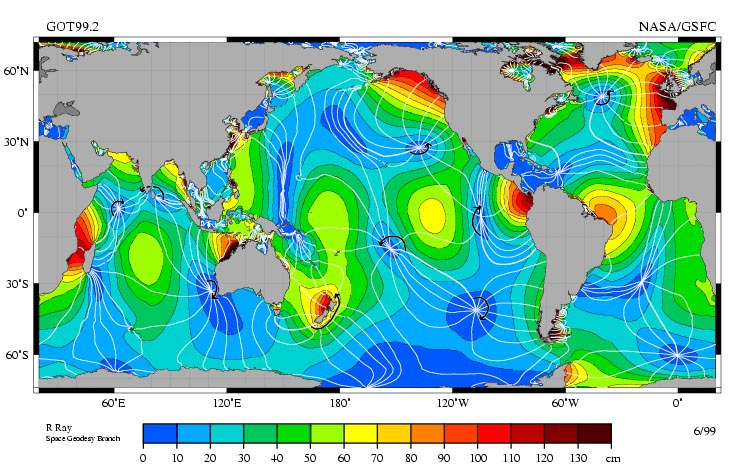
ID:(11638, 0)
Modèle
Top 
Paramètres
Variables
Calculs
Calculs
Calculs
Équations
$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
ID:(15438, 0)
Variation de profondeur dans la direction x (1)
Équation 
Le changement dans l'accélération implique que la colonne d'eau subit une pression différente à moins que la profondeur ne s'ajuste. Pour atteindre un état stable, c'est précisément ce qui se produit. La modification de l'accélération gravitationnelle est compensée par un changement de profondeur correspondant à la marée :
| $ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $ |
Avec la variation du côté de la conjonction avec
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
et avec
| $ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
Il en résulte que la surface s'élève avec en
où seule la partie variable de la variation a été prise en compte, car le terme $GM/d^2$ agit sur tout le système et ne crée pas de différences.
ID:(11653, 1)
Variation de profondeur dans la direction y (1)
Équation 
Le changement d'accélération signifie que la colonne d'eau subit une pression différente à moins que la profondeur ne s'ajuste. Pour atteindre un état stable, c'est précisément ce qui se produit. La modification de l'accélération gravitationnelle est compensée par un changement de profondeur correspondant à la marée :
| $ g h_y = \Delta a_{cy} R $ |
Avec la variation du côté de la conjonction avec
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
En conséquence, la surface s'élève avec à
ID:(11654, 1)
Variation de profondeur dans la direction x (2)
Équation 
Le changement dans l'accélération implique que la colonne d'eau subit une pression différente à moins que la profondeur ne s'ajuste. Pour atteindre un état stable, c'est précisément ce qui se produit. La modification de l'accélération gravitationnelle est compensée par un changement de profondeur correspondant à la marée :
| $ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $ |
Avec la variation du côté de la conjonction avec
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
et avec
| $ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
Il en résulte que la surface s'élève avec en
où seule la partie variable de la variation a été prise en compte, car le terme $GM/d^2$ agit sur tout le système et ne crée pas de différences.
ID:(11653, 2)
Variation de profondeur dans la direction y (2)
Équation 
Le changement d'accélération signifie que la colonne d'eau subit une pression différente à moins que la profondeur ne s'ajuste. Pour atteindre un état stable, c'est précisément ce qui se produit. La modification de l'accélération gravitationnelle est compensée par un changement de profondeur correspondant à la marée :
| $ g h_y = \Delta a_{cy} R $ |
Avec la variation du côté de la conjonction avec
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
En conséquence, la surface s'élève avec à
ID:(11654, 2)
