Utilizador: 
Marés solares e lunares
Storyboard 
O segundo tipo de marés registradas na Terra são as marés solares. Seu tamanho é menor do que o da lua.
ID:(1576, 0)
Profundidade da água necessária para compensar
Imagem
A mudança na aceleração gravitacional leva a um fluxo de água que tende a variar a altura da coluna de água (profundidade do mar) para compensar a pressão:
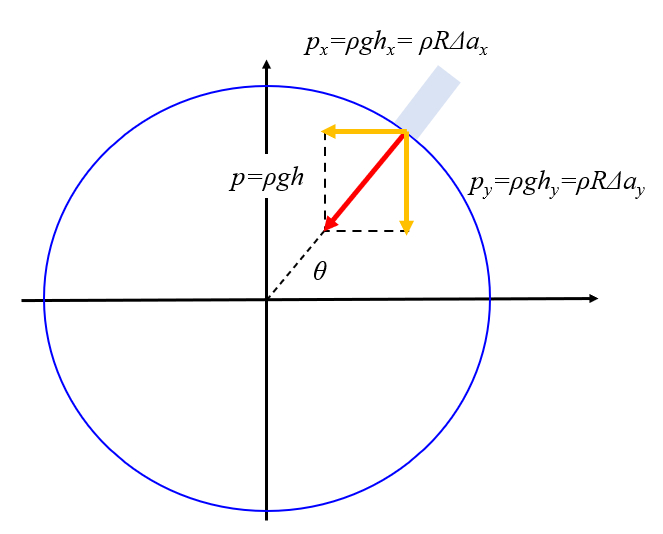
ID:(11652, 0)
Representação como elipse
Imagem
As variações na aceleração levam a mudanças na pressão sobre a água ao redor do planeta, permitindo que as colunas de água difiram em alturas.
Em particular, as desvios causados são os seguintes:
Para o caso do sol: 8,14 cm, 16,28 cm
Para o caso da lua: 17,9 cm, 35,6 cm
Essa situação pode ser representada como uma deformação de um círculo, correspondendo a uma elipse.
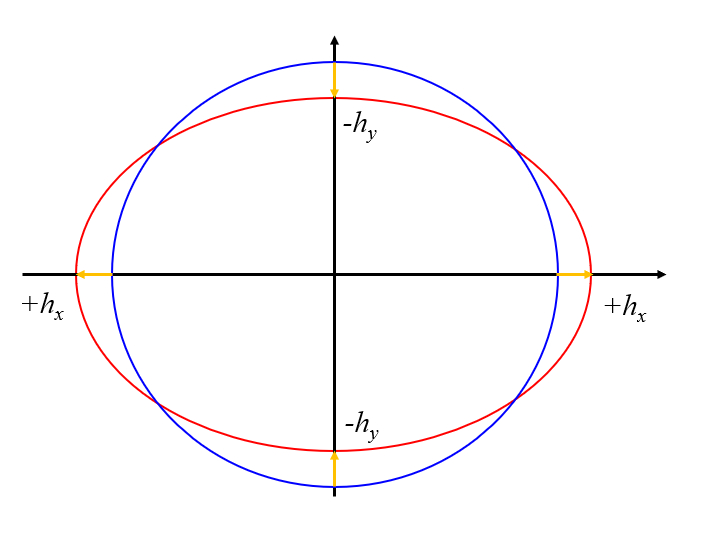
ID:(11657, 0)
Parâmetros do caso Sun
Imagem
No caso do Sol,
os parâmetros considerados são:
Massa: 1,987e+30 kg
Distância Sol-Terra: 1,50e+11 m
As alturas das marés podem ser calculadas com as seguintes relações:
Para a direção x, com aceleração gravitacional $m/s^2$ e raio do planeta $m$, temos:
| $h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $ |
E para a direção y, com aceleração gravitacional $m/s^2$ e raio do planeta $m$, temos:
| $h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$ |
Com o raio da Terra de 6371 km, obtemos que no ponto de menor maré ($\theta = \pi/2$), temos:
$h_y = 8,14 cm$
E no ponto de maior maré ($\theta = 0$), temos:
$h_x = 16,28 cm$
Portanto, as flutuações devido ao Sol são de $h_x + h_y = 24,42 cm$.
ID:(11656, 0)
Parâmetros do caso lunar
Imagem
No caso da lua,
os parâmetros considerados são:
Massa: 7,349e+22 kg
Distância Terra-Lua: 3,84e+8 m
Para a direção x, com , temos:
E para a direção y, com , temos:
Com o raio da Terra de 6371 km, obtemos que no ponto de maré baixa ($\theta = \pi/2$), temos:
$h_y = 17,9 cm$
E no ponto de maré alta ($\theta = 0$), temos:
$h_x = 35,6 cm$
Assim, as flutuações devido à lua são de $h_x + h_y = 53,5 cm$.
ID:(11655, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $
g * h_x = ( Da_cx - Da_ox )* R / 2
$ g h_y = \Delta a_{cy} R $
g * h_y = Da_cy * R
$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $
h_x = 2* G * M * R ^2* cos( theta )/( g * d ^3)
$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$
h_y = G * M * R ^2* sin( theta )/( g * d ^3)
ID:(15437, 0)
Relação de profundidade e variação de aceleração em x
Equação
A mudança na aceleração significa que a coluna de água experimenta uma pressão diferente a menos que a profundidade se ajuste. Para alcançar um estado estacionário, isso é precisamente o que acontece. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
$p_x=\rho g h_x=\rho\displaystyle\frac{1}{2} (\Delta a_{cx} - \Delta a_{ox}) R$
Portanto,
| $ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $ |
ID:(13215, 0)
Variação de profundidade na direção x
Equação
A mudança na aceleração implica que a coluna de água experimenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, isso é precisamente o que acontece. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
| $ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $ |
Com a variação no lado da conjunção com
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
e com
| $ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
Segue-se que a superfície se eleva com em
| $h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $ |
onde apenas a parte variável da variação foi considerada, uma vez que o termo $GM/d^2$ age sobre todo o sistema e não cria diferenças.
ID:(11653, 0)
Relação de profundidade e variação de aceleração em y
Equação
A mudança na aceleração implica que a coluna de água apresenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, é precisamente isso que ocorre. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
$p_y=\rho g h_y=\rho\Delta a_{cy} R$
Portanto, temos:
| $ g h_y = \Delta a_{cy} R $ |
ID:(13216, 0)
Variação de profundidade na direção y
Equação
A mudança na aceleração implica que a coluna de água apresenta uma pressão diferente, a menos que a profundidade se ajuste. Para alcançar um estado estacionário, é precisamente isso que ocorre. A modificação da aceleração gravitacional é compensada por uma mudança na profundidade correspondente à maré:
| $ g h_y = \Delta a_{cy} R $ |
Com a variação no lado da conjunção com
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
Como resultado, a superfície se eleva com em
| $h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$ |
ID:(11654, 0)