Storyboard

Chaque fois que l'on observe depuis un système en rotation (par exemple, la surface de la Terre) un objet se déplaçant en ligne droite à vitesse constante, cela donne l'impression qu'il effectue un mouvement courbe. Cela peut être modélisé en introduisant une force fictive appelée force de Coriolis. Avec cela, nous pouvons comprendre une série de mouvements observés dans l'océan et dans l'atmosphère.

>Modèle

ID:(1521, 0)

Iframe

>Top

ID:(15447, 0)

Video

>Top

Dans la vidéo, on observe qu'un objet semble effectuer un mouvement courbe lorsqu'il est vu depuis un système en rotation. Cependant, depuis un système non rotatif, le mouvement est rectiligne et à vitesse constante.

Pour décrire le mouvement d'un corps se déplaçant en ligne droite depuis un système en rotation, on peut utiliser le subterfuge d'introduire une force fictive (qui n'existe pas) pour rendre compte de ce mouvement. Cette force fictive est appelée dans ce cas la force de Coriolis.

ID:(11671, 0)

Concept

>Top

On établit un système de référence local dans lequel on définit :

• l'axe z pointe vers le haut
• l'axe y pointe vers le nord
• l'axe x pointe vers l'est

Ainsi, le vecteur de la vitesse angulaire de la planète est dans le plan yz avec un angle égal à la latitude du lieu :

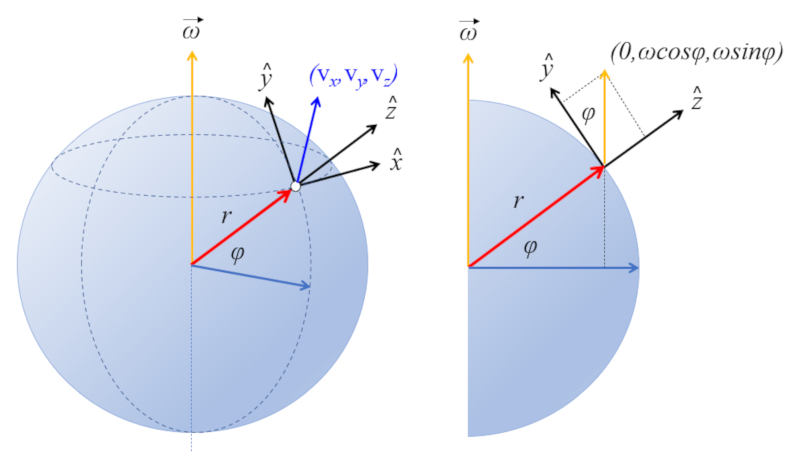
ID:(11672, 0)

Concept

>Top

L'effet du décalage apparent peut être observé particulièrement à la surface de la Terre. Si un objet est lancé depuis l'équateur et qu'il se déplace vers des latitudes plus élevées, il semble "avancer" simplement parce que, à des latitudes plus élevées, la vitesse tangentielle est plus faible que à l'équateur.

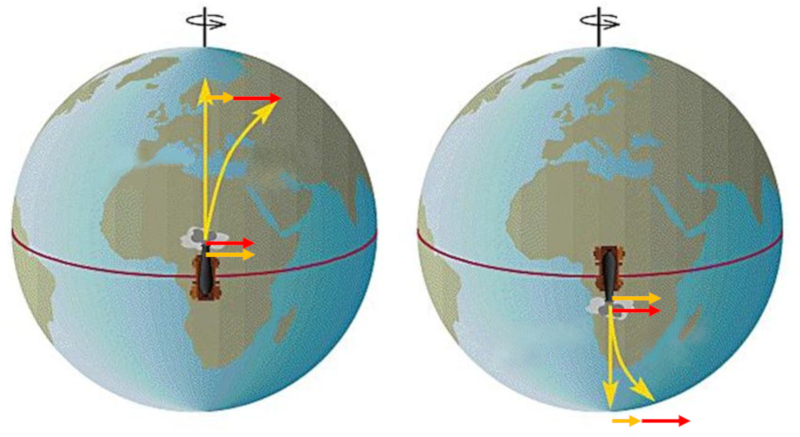
ID:(11673, 0)

Concept

>Top

Si un objet est lancé depuis un endroit éloigné de l'équateur vers l'est, on observe que le corps dévie, restant en arrière en raison de sa vitesse tangentielle plus faible par rapport aux latitudes plus proches de l'équateur.

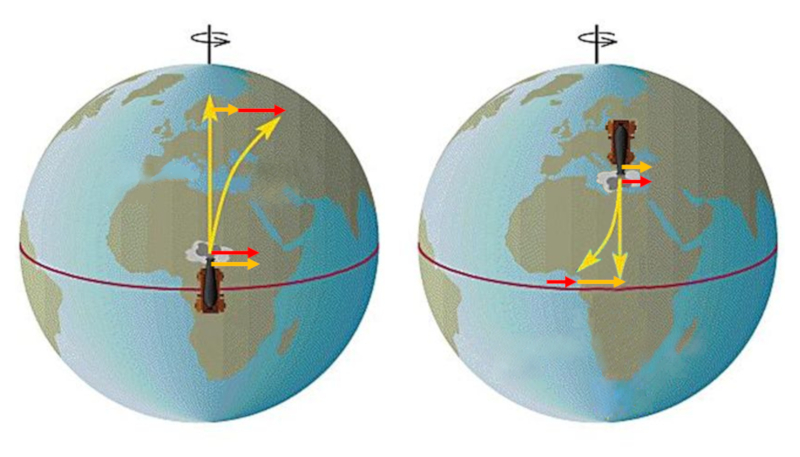
ID:(11674, 0)

Concept

>Top

Si le milieu en mouvement s'écoule depuis un point (par exemple, dans l'air, à partir d'une zone de haute pression), les flux sont retardés ou avancés selon qu'ils se dirigent vers l'équateur ou vers le pôle. Cela conduit à la formation d'un système qui tourne dans le sens négatif (dans l'hémisphère nord), formant ce qu'on appelle un cyclone.

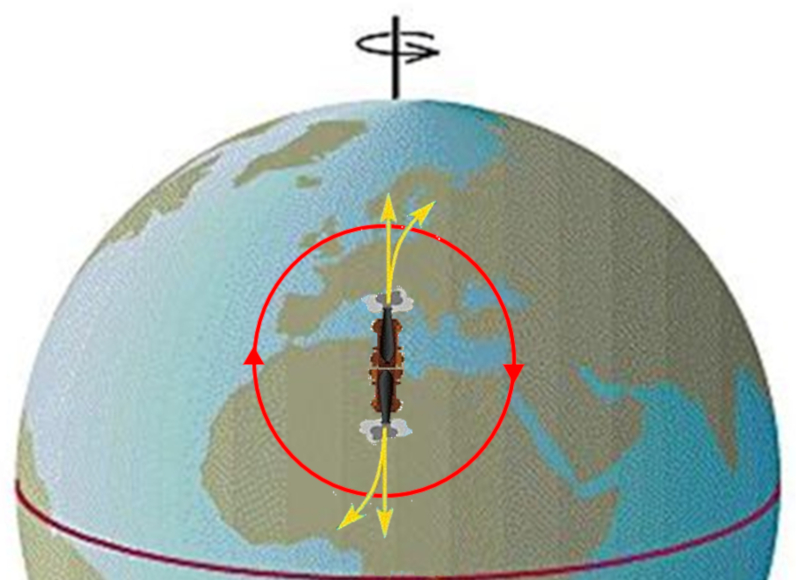
ID:(11669, 0)

Concept

>Top

Si le milieu qui se déplace coule vers un point (par exemple dans l'air, une basse pression), les flux sont avancés/retardés en fonction de s'ils viennent de l'équateur ou du pôle. Cela conduit à la formation d'un système qui tourne dans le sens positif (dans l'hémisphère nord), formant ce qu'on appelle un anticyclone.

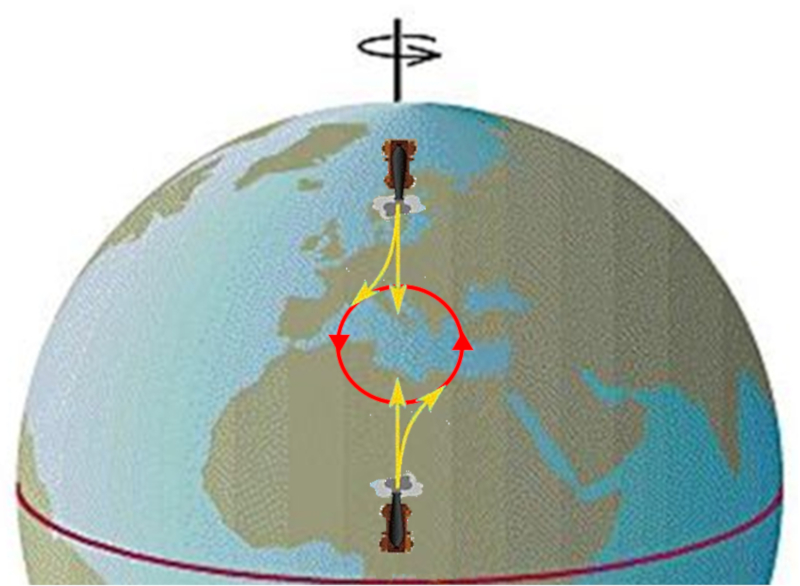
ID:(11675, 0)

Concept

>Top

Si l'on se limite à observer ce qui se passe dans le plan, on constatera que chaque fois que nous nous déplaçons dans une direction particulière, nous subissons une accélération perpendiculaire dans le sens positif. L'amplitude de cette accélération augmente avec la latitude, étant nulle à l'équateur. En dehors de cela, elle est proportionnelle à la vitesse angulaire, ce qui signifie que si le système de référence ne tournait pas, il n'y aurait pas d'effet Coriolis.

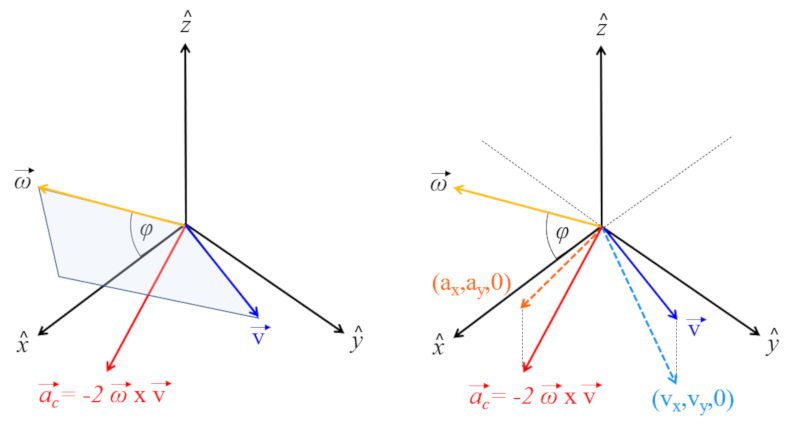
ID:(11692, 0)

Top

>Top

Paramètres

$f$

f

Facteur de Coriolis

rad/s

$\varphi$

phi

Latitude

rad

$\omega$

omega

Vitesse angulaire de la planète

rad/s

Variables

$\vec{a}_c$

&a_c

Accélération de Coriolis

m/s^2

$a_{s,x}$

a_sx

Accélération de Coriolis à la surface, dans la direction x

m/s^2

$a_{s,y}$

a_sy

Accélération de Coriolis à la surface, dans la direction y

m/s^2

$a_{s,z}$

a_sz

Accélération de Coriolis à la surface, dans la direction z

m/s^2

$a_{c,x}$

a_cx

Accélération de Coriolis dans la direction x

m/s^2

$a_{c,y}$

a_cy

Accélération de Coriolis dans la direction y

m/s^2

$a_{c,z}$

a_cz

Accélération de Coriolis dans la direction z

m/s^2

$e$

e

Deuxième facteur de Coriolis

rad/s

$\vec{\omega}$

&omega

Vitesse angulaire

rad/s

$\vec{v}$

&v

Vitesse du corps

m/s

$v_x$

v_x

x vitesse de l'objet

m/s

$v_y$

v_y

y vitesse de l'objet

m/s

$v_z$

v_z

z vitesse de l'objet

m/s

Calculs

• Méthode alternative
• Méthode traditionnelle
• Stratégie
• 2D
• 3D

Équation

Nombre

D'abord, sélectionnez l'équation: à , puis, sélectionnez la variable: à

---

Calculs

Symbole

Équation

Résolu

Traduit

Calculs

Symbole

Équation

Résolu

Traduit

Variable Donnée Calculer Cible : Équation À utiliser

Équations

ID:(15436, 0)

Équation

>Top, >Modèle

L'accélération de Coriolis explique comment un objet dévie de sa trajectoire en raison de la rotation du système de référence.

Il est important de comprendre que la 'force', l''accélération' ou l''effet' de Coriolis est un 'tour de passe-passe' mathématique pour calculer le comportement d'un corps vu depuis un système en rotation. L'équation qui modélise le mieux cet effet est a accélération de Coriolis ($\vec{a}_c$) avec a vitesse angulaire ($\vec{\omega}$) et a vitesse du corps ($\vec{v}$) :

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

Conditions

Variables

$\vec{a}_c$

Accélération de Coriolis

$m/s^2$

8763

$\vec{\omega}$

Vitesse angulaire

$rad/s$

9893

$\vec{v}$

Vitesse du corps

$m/s$

8764

Relation

ID:(11693, 0)

Équation

>Top, >Modèle

A accélération de Coriolis ($\vec{a}_c$) est avec a vitesse angulaire ($\vec{\omega}$) et a vitesse du corps ($\vec{v}$) :

Ainsi, avec a accélération de Coriolis dans la direction x ($a_{c,x}$) associé à A vitesse angulaire de la planète ($\omega$), a y vitesse de l'objet ($v_y$), a z vitesse de l'objet ($v_z$) et a latitude ($\varphi$), la composante x est.

$ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$

Conditions

Variables

$a_{c,x}$

Accélération de Coriolis dans la direction x

$m/s^2$

8597

$\phi$

Latitude

$rad$

8596

$\omega$

Vitesse angulaire de la planète

$rad/s$

8595

$v_y$

y vitesse de l'objet

$m/s$

8513

$v_z$

z vitesse de l'objet

$m/s$

8594

Relation

Développement

À la surface de la Terre, son axe pointe vers le nord avec un angle égal à A latitude ($\varphi$) par rapport au plan. Ainsi, a vitesse angulaire ($\vec{\omega}$) est égal à :

$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$

Et comme a vitesse du corps ($\vec{v}$) est :

$\vec{v}=(v_x,v_y,v_z)$

Donc, la définition de a accélération de Coriolis ($\vec{a}_c$) :

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

donne une composante x égale à :

$ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$

ID:(11694, 0)

Équation

>Top, >Modèle

A accélération de Coriolis ($\vec{a}_c$) est avec a vitesse angulaire ($\vec{\omega}$) et a vitesse du corps ($\vec{v}$) :



Ainsi, avec a accélération de Coriolis dans la direction y ($a_{c,y}$) associé à A vitesse angulaire de la planète ($\omega$), a x vitesse de l'objet ($v_x$) et a latitude ($\varphi$), la composante y est :

$ a_{c,y} = -2 \omega v_x \sin \varphi$

Conditions

Variables

$a_{c,y}$

Accélération de Coriolis dans la direction y

$m/s^2$

8598

$\phi$

Latitude

$rad$

8596

$\omega$

Vitesse angulaire de la planète

$rad/s$

8595

$v_x$

x vitesse de l'objet

$m/s$

8512

Relation

Développement

À la surface de la Terre, son axe pointe vers le nord avec un angle égal à A latitude ($\varphi$) par rapport au plan. Ainsi, a vitesse angulaire ($\vec{\omega}$) est égal à :

$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$

Et comme a vitesse du corps ($\vec{v}$) est :

$\vec{v}=(v_x,v_y,v_z)$

Donc, la définition de a accélération de Coriolis ($\vec{a}_c$) :

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

donne une composante y égale à :

$ a_{c,y} = -2 \omega v_x \sin \varphi$

ID:(11695, 0)

Équation

>Top, >Modèle

A accélération de Coriolis ($\vec{a}_c$) est avec a vitesse angulaire ($\vec{\omega}$) et a vitesse du corps ($\vec{v}$) :



Ainsi, avec a accélération de Coriolis dans la direction z ($a_{c,z}$) associé à A vitesse angulaire de la planète ($\omega$), a x vitesse de l'objet ($v_x$) et a latitude ($\varphi$), la composante y est :

$ a_{c,z} = 2 \omega v_x \cos \varphi$

Conditions

Variables

$a_{c,z}$

Accélération de Coriolis dans la direction z

$m/s^2$

8599

$\phi$

Latitude

$rad$

8596

$\omega$

Vitesse angulaire de la planète

$rad/s$

8595

$v_x$

x vitesse de l'objet

$m/s$

8512

Relation

Développement

À la surface de la Terre, son axe pointe vers le nord avec un angle égal à A latitude ($\varphi$) par rapport au plan. Ainsi, a vitesse angulaire ($\vec{\omega}$) est égal à :

$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$

Et comme a vitesse du corps ($\vec{v}$) est :

$\vec{v}=(v_x,v_y,v_z)$

Donc, la définition de a accélération de Coriolis ($\vec{a}_c$) :

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

donne une composante z égale à :

$ a_{c,z} = 2 \omega v_x \cos \varphi$

ID:(11696, 0)

Équation

>Top, >Modèle

Pour simplifier les équations, nous travaillons avec un facteur de Coriolis ($f$), qui est une constante pour l'emplacement physique, car elle inclut a vitesse angulaire de la planète ($\omega$) pour la Terre et a latitude ($\varphi$) pour l'emplacement :

$ f = 2 \omega \sin \varphi $

Conditions

Variables

$f$

Facteur de Coriolis

$rad/s$

8600

$\phi$

Latitude

$rad$

8596

$\omega$

Vitesse angulaire de la planète

$rad/s$

8595

Relation

Dans l'hémisphère sud, la latitude est négative, et avec elle, 8600, ce qui explique pourquoi les systèmes tournent dans le sens opposé à l'hémisphère nord.

ID:(11697, 0)

Équation

>Top, >Modèle

Pour simplifier les équations, nous travaillons avec un deuxième facteur de Coriolis ($e$), qui est une constante pour l'emplacement physique, car elle inclut a vitesse angulaire de la planète ($\omega$) pour la Terre et a latitude ($\varphi$) pour l'emplacement :

$ e = 2 \omega \cos \varphi $

Conditions

Variables

$e$

Deuxième facteur de Coriolis

$rad/s$

10273

$\varphi$

Latitude

$rad$

8596

$\omega$

Vitesse angulaire de la planète

$rad/s$

8595

Relation

ID:(15450, 0)

Équation

>Top, >Modèle

Comme a accélération de Coriolis dans la direction x ($a_{c,x}$) peut être réécrit avec le facteur de Coriolis ($f$) et la condition qu'il n'y a pas de mouvement vertical :

$v_z = 0$

il en résulte que a accélération de Coriolis à la surface, dans la direction x ($a_{s,x}$) est :

$ a_{s,x} = f v_y $

Conditions

Variables

$a_{s,x}$

Accélération de Coriolis à la surface, dans la direction x

$m/s^2$

8601

$f$

Facteur de Coriolis

$rad/s$

8600

$v_y$

y vitesse de l'objet

$m/s$

8513

Relation

Développement

Comme a accélération de Coriolis dans la direction x ($a_{c,x}$) est composé de a vitesse angulaire de la planète ($\omega$), a latitude ($\varphi$), a y vitesse de l'objet ($v_y$) et a z vitesse de l'objet ($v_z$) :

$ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$

et la définition de le facteur de Coriolis ($f$) est :

$ f = 2 \omega \sin \varphi $

ainsi que la contrainte de mouvement à la surface où :

$v_z = 0$

il en résulte que a accélération de Coriolis dans la direction x ($a_{c,x}$) est :

$ a_{s,x} = f v_y $

ID:(11698, 0)

Équation

>Top, >Modèle

Comme a accélération de Coriolis dans la direction x ($a_{c,x}$) peut être réécrit avec le facteur de Coriolis ($f$) et sous la condition qu'il n'y ait pas de mouvement vertical :

$v_z = 0$

Ainsi, on déduit que a accélération de Coriolis à la surface, dans la direction y ($a_{s,y}$) est :

$ a_{s,y} = - f v_x $

Conditions

Variables

$a_{s,y}$

Accélération de Coriolis à la surface, dans la direction y

$m/s^2$

8602

$f$

Facteur de Coriolis

$rad/s$

8600

$v_x$

x vitesse de l'objet

$m/s$

8512

Relation

Développement

Comme a accélération de Coriolis dans la direction y ($a_{c,y}$) est composé de a vitesse angulaire de la planète ($\omega$), a x vitesse de l'objet ($v_x$) et a latitude ($\varphi$) :

$ a_{c,y} = -2 \omega v_x \sin \varphi$

et que la définition de le facteur de Coriolis ($f$) est :

$ f = 2 \omega \sin \varphi $

en plus de la contrainte d'un mouvement à la surface où :

$v_z = 0$

cela conduit à ce que a accélération de Coriolis dans la direction y ($a_{c,y}$) soit :

$ a_{s,y} = - f v_x $

ID:(11699, 0)

Équation

>Top, >Modèle

Comme a accélération de Coriolis dans la direction z ($a_{c,z}$) peut être réécrit avec le deuxième facteur de Coriolis ($e$) et sous la condition qu'il n'y ait pas de mouvement vertical :

$v_z = 0$

Ainsi, on déduit que a accélération de Coriolis à la surface, dans la direction z ($a_{s,z}$) est :

$ a_{s,z} = e v_x $

Conditions

Variables

$a_{s,z}$

Accélération de Coriolis à la surface, dans la direction z

$m/s^2$

10274

$e$

Deuxième facteur de Coriolis

$rad/s$

10273

$v_x$

x vitesse de l'objet

$m/s$

8512

Relation

Développement

Comme a accélération de Coriolis dans la direction y ($a_{c,y}$) est composé de a vitesse angulaire de la planète ($\omega$), a x vitesse de l'objet ($v_x$) et a latitude ($\varphi$) :

$ a_{c,y} = -2 \omega v_x \sin \varphi$

et que la définition de le deuxième facteur de Coriolis ($e$) est :

$ e = 2 \omega \cos \varphi $

en plus de la contrainte d'un mouvement à la surface où :

$v_z = 0$

cela conduit à ce que a accélération de Coriolis à la surface, dans la direction z ($a_{s,z}$) soit :

$ a_{s,z} = e v_x $

ID:(15451, 0)