Usuario: 
Sonar
Storyboard 
Otro de los usos del sonido en el agua son los sonares, tanto como herramienta tecnológica como técnica utilizada por ballenas y delfines (biosonares) para determinar distancias.
El biosonar se emplea tanto para navegar como para cazar, estimando distancias e incluso velocidades para prever el movimiento que tendrá la presa en el futuro.
ID:(1597, 0)
Principio del sonar
Imagen
El principio del sonar es la emisión de sonido que luego se refleja en el objeto a estudiar y finalmente se capta por el emisor. Del tiempo de viaje de la onda de sonido y la velocidad en el medio se determina la distancia de este.
Existen tres situaciones de interés:
• Emisor y reflector están en reposo
• Emisor en movimiento y reflector en reposo
• Emisor y reflector en reposo
ID:(11869, 0)
Emisor y reflector están en reposo
Concepto
Cuando tanto el emisor como el reflector no se desplazan, la distancia que recorre el sonido es igual a dos veces la distancia emisor y reflector están en reposo ($d$):
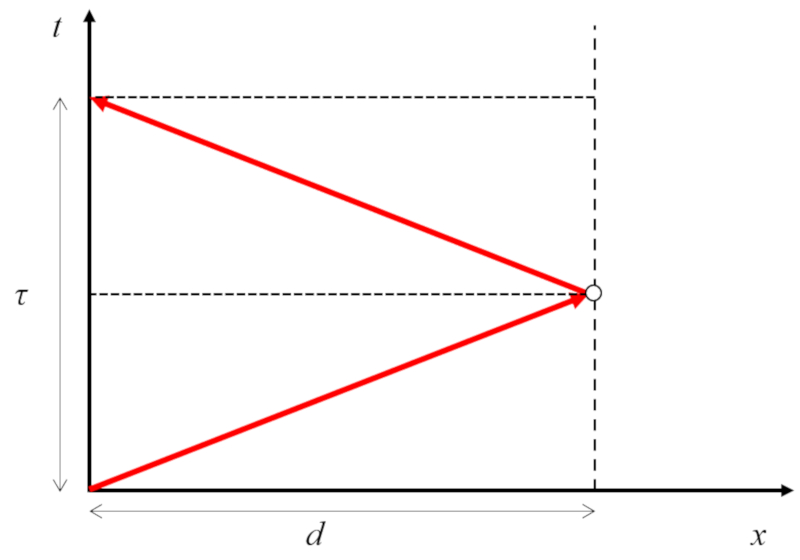
Dado que la distancia se recorre a la velocidad del sonido ($c$) en el tiempo de eco ($\tau_1$), tenemos que la distancia emisor y reflector están en reposo ($d$) es:
| $ d = \displaystyle\frac{1}{2} c \tau_1 $ |
ID:(11870, 0)
Emisor en movimiento y reflector en reposo
Concepto
En el caso en que el emisor se desplace a una velocidad la velocidad del emisor ($v_e$) y el reflector esté en reposo, la distancia inicial reflector ($d_0$) varía según el sonido que viaja con la velocidad del sonido ($c$) requiera de el tiempo de eco ($\tau_1$) ya sea mayor (si los cuerpos se alejan) o menor (si los cuerpos se acercan):
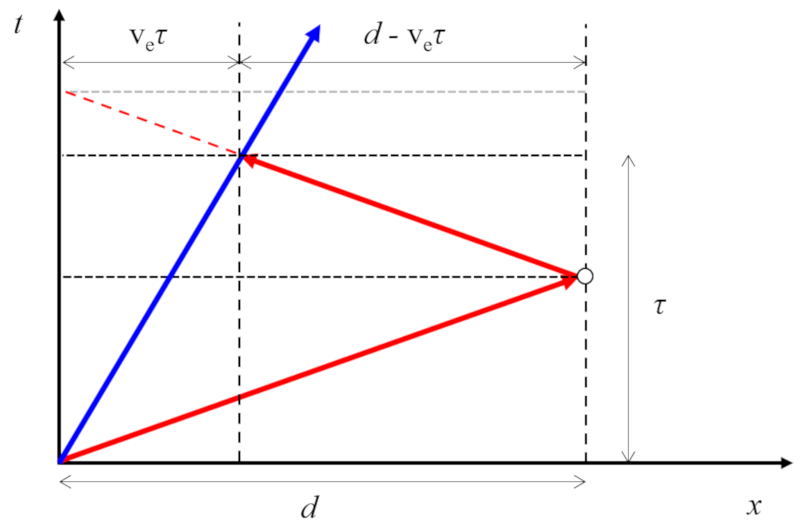
Por lo tanto, la distancia inicial reflector ($d_0$) es igual a
| $ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $ |
y la posición del reflector respecto al emisor es
| $ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $ |
en función de el tiempo desde el inicio del rastreo ($t$).
ID:(11871, 0)
Emisor y reflector en movimiento
Concepto
En el caso de que el emisor se desplace a una velocidad de la velocidad del emisor ($v_e$) y el reflector se desplace a una velocidad de la velocidad del reflector o receptor ($v_o$), la distancia entre el emisor y el reflector puede ser mayor ($v_e > v_o$) o menor ($v_e < v_o$). Si representamos esta situación incluyendo el tiempo de eco ($\tau_1$), el tiempo del segundo eco ($\tau_2$) y el tiempo entre pulsos ($\tau$), obtenemos:
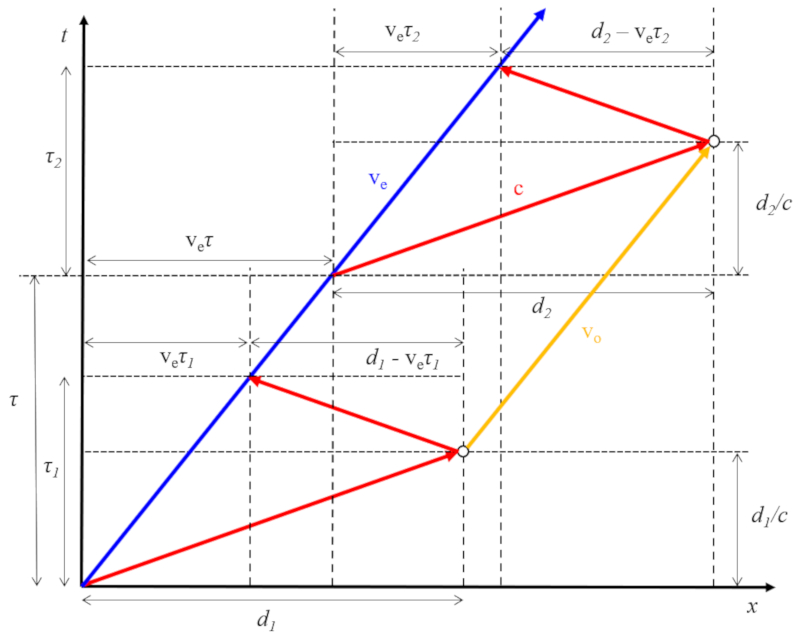
Al calcular el camino recorrido y el tiempo transcurrido por el reflector entre ambos pulsos, se obtiene la velocidad del reflector o receptor ($v_o$) de la siguiente manera:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
Conocidos tanto la velocidad del emisor ($v_e$) como la velocidad del reflector o receptor ($v_o$), podemos expresar la posición relativa emisor en movimiento y reflector en reposo ($x$) en función de el tiempo desde el inicio del rastreo ($t$) de la siguiente manera:
| $ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$ |
con la velocidad del sonido ($c$).
ID:(11872, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ d = \displaystyle\frac{1}{2} c \tau_1 $
d = c * tau_1 /2
$ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $
d_0 =( c + v_e )* tau_1 /2
$ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$
v_o = c *( 2* v_e * tau + ( c + v_e )*( tau_2 - tau_1 ))/(2* c * tau + ( c + v_e )*( tau_2 - tau_1 ))
$ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $
x = ( c + v_e )* tau_1 /2 - v_e * t
$ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$
x =((2* tau * tau_1 +( tau_2 - tau_1 )* t )*( c - v_e )*( v_e + c ))/(( v_e + c )*( tau_2 - tau_1 ) + 2* c * tau ))
ID:(15469, 0)
Distancia emisor y reflector están en reposo
Ecuación
Si no hay movimiento, el tiempo que la señal el tiempo de eco ($\tau_1$) tarda en recorrer la distancia a la velocidad del sonido la velocidad del sonido ($c$) es $c \tau$, que es el doble de la distancia entre el emisor y el reflector.
Por lo tanto, la distancia emisor y reflector están en reposo ($d$) es:
| $ d = \displaystyle\frac{1}{2} c \tau_1 $ |
ID:(11873, 0)
Distancia emisor en movimiento y reflector en reposo
Ecuación
En el caso de que el emisor se desplaza a una velocidad la velocidad del emisor ($v_e$) y el reflector no se mueve, su distancia inicial la distancia inicial reflector ($d_0$) se puede estimar mediante el tiempo del eco el tiempo de eco ($\tau_1$). En este tipo, la distancia recorrida es igual a $c \tau_1$, que es igual a la distancia inicial entre el emisor y el reflector la distancia inicial reflector ($d_0$), y el regreso, que es igual a lo mismo, $d_0$ menos la distancia recorrida por el emisor $v_e\tau_1$. Por ello, se tiene que
$d_0 + d_0 - v_e\tau_1 = c\tau_1$
o que la distancia inicial reflector ($d_0$) es:
| $ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $ |
ID:(11874, 0)
Posición relativa emisor en movimiento y reflector en reposo
Ecuación
Para determinar la posición relativa emisor en movimiento y reflector en reposo ($x$), se debe considerar la distancia inicial reflector ($d_0$) y restar el camino recorrido por el emisor. Este último se calcula a partir de la velocidad del emisor ($v_e$) y el tiempo desde el inicio del rastreo ($t$), lo que resulta en:
| $ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $ |
ID:(11876, 0)
Velocidad del reflector en movimiento
Ecuación
La velocidad del reflector o receptor ($v_o$) se puede calcular a partir de la velocidad del emisor ($v_e$) y la velocidad del sonido ($c$), así como el tiempo de eco ($\tau_1$), el tiempo del segundo eco ($\tau_2$) y el tiempo entre pulsos ($\tau$), utilizando la fórmula:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
Con la distancia al objeto al emitir primer señal ($d_1$) y la velocidad del sonido ($c$), se puede estimar el tiempo en que la primera señal se refleja como $d_1/c$, y con la distancia al objeto al emitir segunda señal ($d_2$), el segundo tiempo como $\tau + d_2/c$. Por lo tanto, el tiempo entre los reflejos de las dos señales es:
$\Delta\tau = \tau + \displaystyle\frac{ d_2 }{ c } - \displaystyle\frac{ d_1 }{ c }$
La posición en la que la señal se refleja por primera vez es la distancia al objeto al emitir primer señal ($d_1$), y la segunda en ($$). Por lo tanto, la distancia recorrida por el reflector es:
$ \Delta x = v_e \tau + d_2 - d_1 $
Así, la velocidad del reflector es:
$v_o=\displaystyle\frac{\Delta x}{\Delta t}=\displaystyle\frac{ v_e\tau + d_2 - d_1}{ \tau + \displaystyle\frac{d_2}{c} - \displaystyle\frac{d_1}{c}}$
Como se mencionó anteriormente en distancia inicial reflector $m$, tiempo de eco $s$, velocidad del emisor $m/s$ y velocidad del sonido $m/s$, la diferencia entre las distancias recorridas es:
$d_2-d_1=\displaystyle\frac{1}{2}( c + v_e )( \tau_2 - \tau_1 )$
y la velocidad resultante es:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
ID:(11877, 0)
Distancia emisor y reflector en movimiento
Ecuación
La posición relativa emisor en movimiento y reflector en reposo ($x$) se puede calcular de la velocidad del emisor ($v_e$), el tiempo de eco ($\tau_1$), el tiempo del segundo eco ($\tau_2$) y el tiempo entre pulsos ($\tau$) mediante
| $ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$ |
Para calcular la posición relativa entre emisor y reflector se debe describir primero la posición del reflector y luego restar la del emisor. Este ultimo se mueve a una velocidad la velocidad del emisor ($v_e$) en un medio en que el sonido se propaga con la velocidad del sonido ($c$) por lo que su posición es en el tiempo desde el inicio del rastreo ($t$) igual a $v_et$. La posición del reflector en el tiempo $d_1/c$ a una distancia $d_1$ por lo que con la velocidad la velocidad del reflector o receptor ($v_o$) se tiene
$d_1 + v_o\left(t - \displaystyle\frac{d_1}{c}\right) = v_ot + d_1\left(1 -\displaystyle\frac{v_o}{c}\right)=v_ot + \left(1 -\displaystyle\frac{v_o}{c}\right)\left(1 +\displaystyle\frac{v_e}{c}\right)c\tau_1$
Como el emisor reduce la distancia en el tiempo según
$v_et$
se tiene que la posición relativa emisor en movimiento y reflector en reposo ($x$) es
$x = (v_o- v_e)t + \left(1 -\displaystyle\frac{v_o}{c}\right)\left(1 +\displaystyle\frac{v_e}{c}\right)c\tau_1$
Si finalmenge se empela la expresión para la velocidad del reflector o receptor ($v_o$)
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
se tiene la expresión final
| $ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$ |
ID:(11875, 0)