Usuario: 
Velocidad del sonido en el mar
Storyboard 
La velocidad del sonido en el mar depende de la presión, temperatura y salinidad.
ID:(1548, 0)
Velocidad del sonido con la profundidad
Concepto
La velocidad del sonido en el océano varia con la profundidad según se muestra en la gráfica:
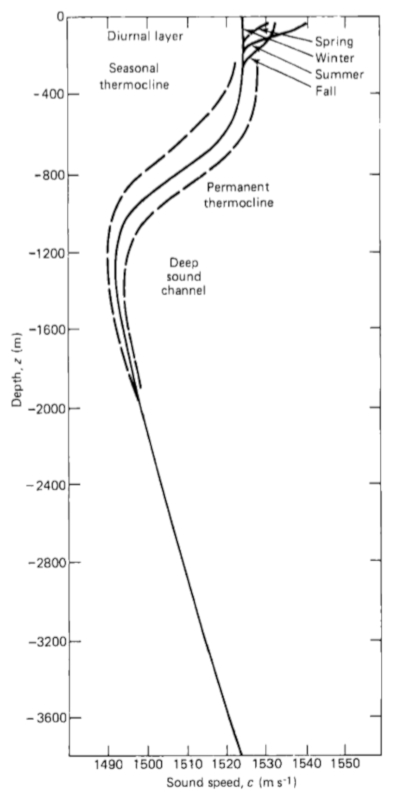
La forma del curva puede ir variando según la época del año.
ID:(11814, 0)
Dependencia de la velocidad del sonido
Concepto
La velocidad del sonido en el océano depende de la temperatura y de la presión como se muestra en la gráfica:
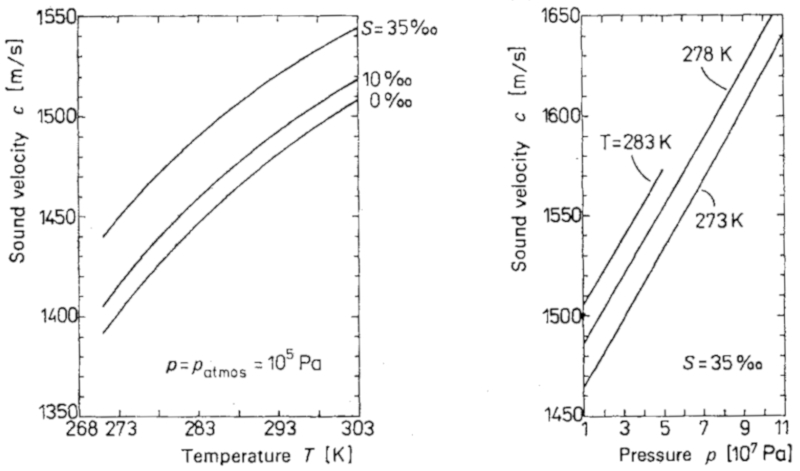
ID:(11815, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
c = c_0 T ^3- c_1 T ^2+( c_3 - c_2 s ) T + c_4 p + c_5 s - c_6
c = c_0 * T ^3- c_1 * T ^2+( c_3 - c_2 * s )* T + c_4 * p +c_5 * s - c_6
\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }
sin( theta_i )/sin( theta_r )= c_i / c_e
ID:(15465, 0)
Ley de Snell en función de la velocidad
Ecuación
La relación entre los ángulos de incidencia y refractados indicados en la siguiente gráfica
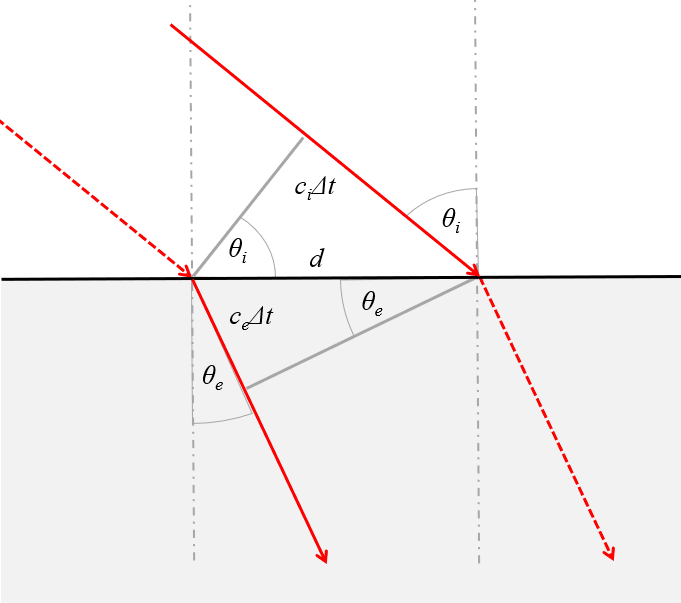
se pueden escribir en función de la velocidad de la luz en cada medio
| \displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e } |
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}
y\\n\\n
\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}
\\n\\nSi se despeja en ambas ecuaciones la distancia
d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}
por lo que se tiene que
| \displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e } |
ID:(3342, 0)
Ecuación de la velocidad del sonido
Ecuación
En 1977, Clay y Medwin desarrollaron un modelo para estimar la velocidad del sonido en función de la temperatura, salinidad y presión.
Se puede estimar la velocidad del sonido (c) en función de la presión hidrostatica (p), la temperatura (T) y la salinidad (s) mediante la siguiente expresión:
| c = c_0 T ^3- c_1 T ^2+( c_3 - c_2 s ) T + c_4 p + c_5 s - c_6 |
donde c_i son constantes empíricas.
Referencia: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah y Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, No. 22, Noviembre 2017.
ID:(11816, 0)