Storyboard

Another use of sound in water is sonar, employed both as a technological tool and as a technique used by whales and dolphins (biosonar) to determine distances.

Biosonar is used for navigation and hunting, estimating distances and even velocities to predict the future movement of prey.

>Model

ID:(1597, 0)

Iframe

>Top

ID:(15468, 0)

Image

>Top

The principle of sonar is the emission of sound that is then reflected in the object to be studied and is finally captured by the emitter. The distance of the sound wave is determined from the travel time of the sound wave and the speed in the medium.

There are three situations of interest:

• Emitter and reflector are at rest

• Emitter in motion and reflector at rest

• Emitter and reflector at rest

ID:(11869, 0)

Concept

>Top

In the case where both the transmitter and the reflector remain stationary, the path traveled by the sound is equal to twice the emitter and reflector distance are at rest ($d$):

Since the distance is covered at the speed of sound ($c$) in the echo time ($\tau_1$), we have that the emitter and reflector distance are at rest ($d$) is:

ID:(11870, 0)

Concept

>Top

In the case where the transmitter moves at a velocity the emitter speed ($v_e$) and the reflector is at rest, the reflector starting distance ($d_0$) varies depending on whether the sound traveling at the speed of sound ($c$) requires the echo time ($\tau_1$) to be greater (if the bodies move apart) or smaller (if the bodies move closer):

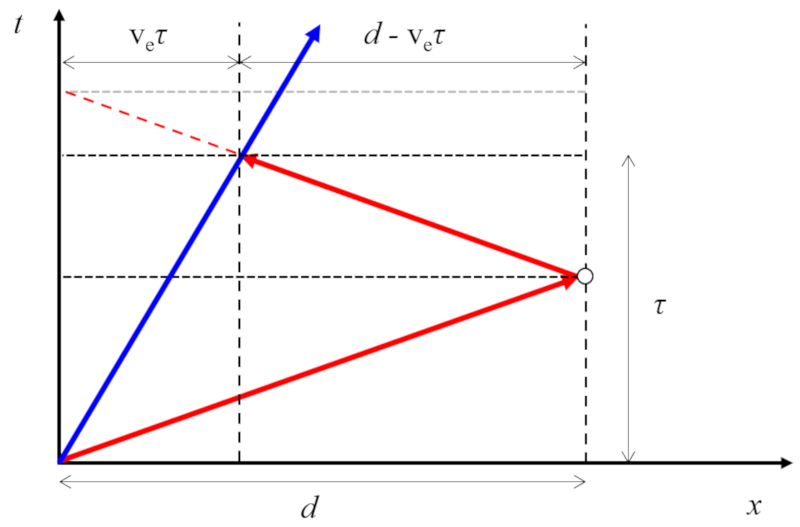
Therefore, the reflector starting distance ($d_0$) is equal to

and the position of the reflector relative to the transmitter is

as a function of the time from start of trace ($t$).

ID:(11871, 0)

Concept

>Top

In the case where the emitter moves at a speed of the emitter speed ($v_e$) and the reflector moves at a speed of the reflector or receiver speed ($v_o$), the distance between the emitter and the reflector can be either greater ($v_e > v_o$) or smaller ($v_e < v_o$). If we represent this situation including the echo time ($\tau_1$), the second echo time ($\tau_2$), and the time between pulses ($\tau$), we obtain:

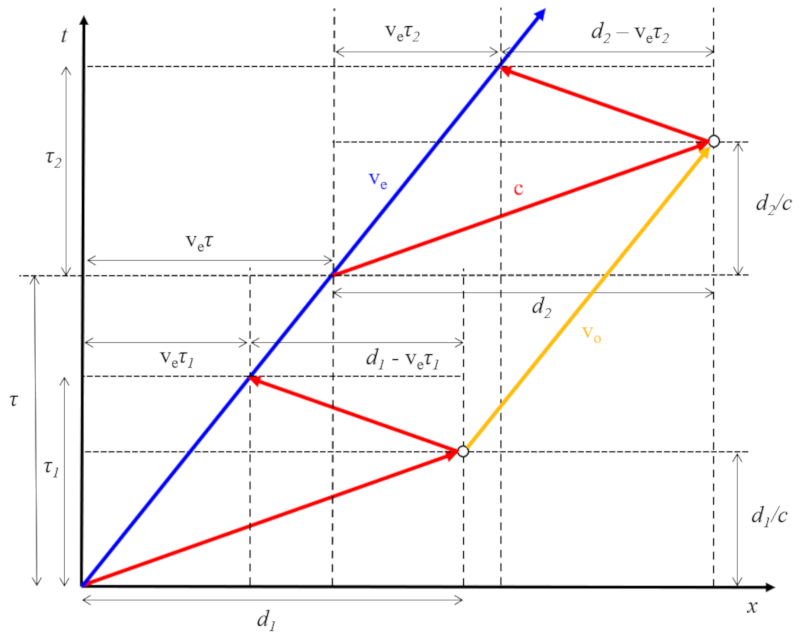
By calculating the distance traveled and the time elapsed by the reflector between both pulses, we obtain the reflector or receiver speed ($v_o$) as follows:

Knowing both the emitter speed ($v_e$) and the reflector or receiver speed ($v_o$), we can express the relative position emitter in motion and reflector at rest ($x$) in terms of the time from start of trace ($t$) as follows:

with the speed of sound ($c$).

ID:(11872, 0)

Top

>Top

Parameters

$d$

d

Emitter and reflector distance are at rest

m

$c$

c

Speed of sound

m/s

Variables

$\tau_1$

tau_1

Echo time

s

$v_e$

v_e

Emitter speed

m/s

$v_o$

v_o

Reflector or receiver speed

m/s

$d_0$

d_0

Reflector starting distance

m

$x$

x

Relative position emitter in motion and reflector at rest

m

$\tau_2$

tau_2

Second echo time

s

$\tau$

tau

Time between pulses

s

$t$

t

Time from start of trace

s

Calculations

• Alternative method
• Traditional method
• Strategy
• 2D
• 3D

Equation

Number

First, select the equation: to , then, select the variable: to

---

Calculations

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable Given Calculate Target : Equation To be used

Equations

ID:(15469, 0)

Equation

>Top, >Model

If there is no movement, the time required for signal the echo time ($\tau_1$) to travel at the speed of sound the speed of sound ($c$) is $c \tau$, which is twice the distance between the transmitter and the reflector.

Therefore, the emitter and reflector distance are at rest ($d$) is:

$d = \displaystyle\frac{1}{2} c \tau_1$

Conditions

Variables

$\tau_1$

Echo time

$s$

8650

$d$

Emitter and reflector distance are at rest

$m$

9911

$c$

Speed of sound

$m/s$

8652

Relation

ID:(11873, 0)

Equation

>Top, >Model

In the case where the emitter moves at a speed of the emitter speed ($v_e$) and the reflector remains stationary, its initial distance the reflector starting distance ($d_0$) can be estimated using the echo time the echo time ($\tau_1$). In this scenario, the distance traveled equals $c \tau_1$, which is equal to the initial distance between the emitter and reflector the reflector starting distance ($d_0$), plus the return trip, which is the same $d_0$ minus the distance traveled by the emitter $v_e\tau_1$. Hence, we have:

$d_0 + d_0 - v_e\tau_1 = c\tau_1$

or that the reflector starting distance ($d_0$) is:

$d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1$

Conditions

Variables

$\tau_1$

Echo time

$s$

8650

$v_e$

Emitter speed

$m/s$

8653

$d_0$

Reflector starting distance

$m$

8649

$c$

Speed of sound

$m/s$

8652

Relation

ID:(11874, 0)

Equation

>Top, >Model

To determine the relative position emitter in motion and reflector at rest ($x$), one must consider the reflector starting distance ($d_0$) and subtract the path traveled by the emitter. This latter is calculated from the emitter speed ($v_e$) and the time from start of trace ($t$), resulting in:

$x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t$

Conditions

Variables

$v_e$

Emitter speed

$m/s$

8653

$x$

Relative position emitter in motion and reflector at rest

$m$

9912

$c$

Speed of sound

$m/s$

8652

$t$

Time from start of trace

$s$

8520

Relation

ID:(11876, 0)

Equation

>Top, >Model

The reflector or receiver speed ($v_o$) can be calculated from the emitter speed ($v_e$) and the speed of sound ($c$), along with the echo time ($\tau_1$), the second echo time ($\tau_2$), and the time between pulses ($\tau$), using the formula:

$v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$

Conditions

Variables

$\tau_1$

Echo time

$s$

8650

$v_e$

Emitter speed

$m/s$

8653

$v_o$

Reflector or receiver speed

$m/s$

8654

$\tau_2$

Second echo time

$s$

8651

$c$

Speed of sound

$m/s$

8652

$\tau$

Time between pulses

$s$

8657

Relation

Development

With the distance to the object when emitting first signal ($d_1$) and the speed of sound ($c$), one can estimate the time at which the first signal reflects as $d_1/c$, and with the distance to the object when emitting second signal ($d_2$), the second time as $\tau + d_2/c$. Therefore, the time between the reflections of the two signals is given by:

$\Delta\tau = \tau + \displaystyle\frac{ d_2 }{ c } - \displaystyle\frac{ d_1 }{ c }$

The position where the first signal reflects is the distance to the object when emitting first signal ($d_1$), and the second is ($$). Hence, the distance traveled by the reflector is:

$\Delta x = v_e \tau + d_2 - d_1$

Thus, the velocity of the reflector is:

$v_o=\displaystyle\frac{\Delta x}{\Delta t}=\displaystyle\frac{ v_e\tau + d_2 - d_1}{ \tau + \displaystyle\frac{d_2}{c} - \displaystyle\frac{d_1}{c}}$

As mentioned earlier in echo time $s$, emitter speed $m/s$, reflector starting distance $m$ and speed of sound $m/s$, the difference between the distances traveled is given by:

$d_2-d_1=\displaystyle\frac{1}{2}( c + v_e )( \tau_2 - \tau_1 )$

and the resulting velocity is:

$v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$

ID:(11877, 0)

Equation

>Top, >Model

Para calcular la posición relativa entre emisor y reflector se debe describir primero la posición del reflector y luego restar la del emisor. Este ultimo se mueve a una velocidad v_e por lo que su posición es v_et. La posición del reflector en el tiempo d_1/c a una distancia d_1 por lo que con la velocidad v_o se tiene

$d_1 + v_o\left(t - \displaystyle\frac{d_1}{c}\right) = v_ot + d_1\left(1 -\displaystyle\frac{v_o}{c}\right)=v_ot + \left(1 -\displaystyle\frac{v_o}{c}\right)\left(1 +\displaystyle\frac{v_e}{c}\right)c\tau_1$

Como el emisor reduce la distancia en el tiempo según

$v_et$

se tiene que la distancia efectiva entre objeto y emisor es con

$x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$

Conditions

Variables

$\tau_1$

Echo time

$s$

8650

$v_e$

Emitter speed

$m/s$

8653

$x$

Relative position emitter in motion and reflector at rest

$m$

9912

$\tau_2$

Second echo time

$s$

8651

$c$

Speed of sound

$m/s$

8652

$\tau$

Time between pulses

$s$

8657

Relation

ID:(11875, 0)