Benützer: 
Sonar
Storyboard 
Eine weitere Verwendung von Schall im Wasser sind Sonare, sowohl als technologisches Werkzeug als auch als Technik, die von Walen und Delfinen (Biosonaren) verwendet wird, um Entfernungen zu bestimmen.
Biosonar wird sowohl zur Navigation als auch zur Jagd eingesetzt, um Entfernungen und sogar Geschwindigkeiten abzuschätzen und die zukünftige Bewegung der Beute vorherzusagen.
ID:(1597, 0)
Sonarprinzip
Bild
Das Prinzip des Sonars ist die Schallemission, die dann im zu untersuchenden Objekt reflektiert und schließlich vom Emitter erfasst wird. Die Entfernung der Schallwelle wird aus der Laufzeit der Schallwelle und der Geschwindigkeit im Medium bestimmt.
Es gibt drei interessante Situationen:
• Emitter und Reflektor ruhen
• Emitter in Bewegung und Reflektor in Ruhe
• Emitter und Reflektor in Ruhe
ID:(11869, 0)
Sender und Reflektor ruhen
Konzept
Im Falle, dass sowohl der Sender als auch der Reflektor sich nicht bewegen, ist der Weg, den der Ton zurücklegt, gleich zweimal die Emitter- und Reflektorabstand sind in Ruhe ($d$):
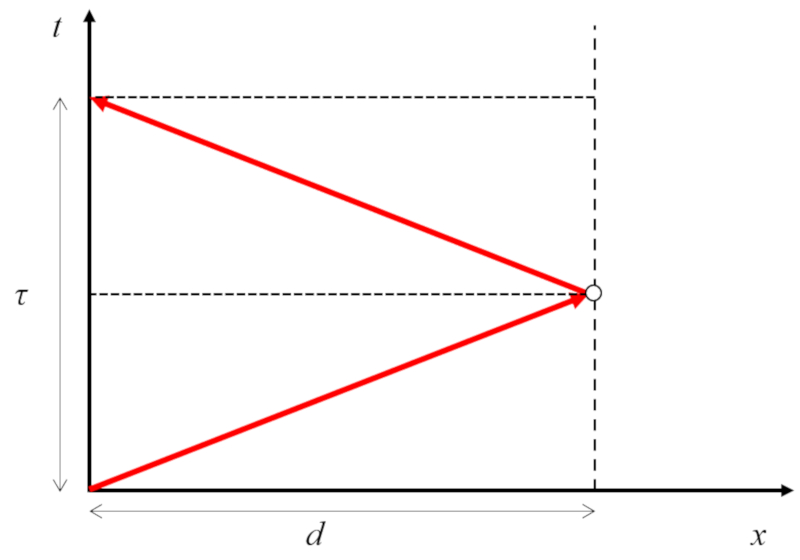
Da der Weg mit die Schallgeschwindigkeit ($c$) in der Echozeit ($\tau_1$) zurückgelegt wird, haben wir, dass die Emitter- und Reflektorabstand sind in Ruhe ($d$) ist:
| $ d = \displaystyle\frac{1}{2} c \tau_1 $ |
ID:(11870, 0)
Sender in Bewegung und Reflektor in Ruhe
Konzept
Im Fall, dass sich der Sender mit einer Geschwindigkeit von die Emittergeschwindigkeit ($v_e$) bewegt und der Reflektor ruht, variiert die Reflektorstartabstand ($d_0$) je nachdem, ob der Ton, der mit die Schallgeschwindigkeit ($c$) reist, der Echozeit ($\tau_1$) erfordert, sei es größer (wenn sich die Körper voneinander entfernen) oder kleiner (wenn sich die Körper annähern):
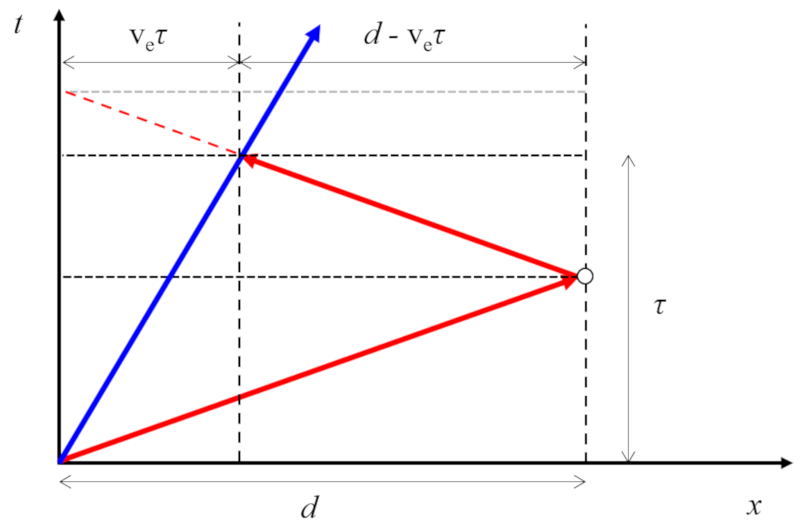
Daher ist die Reflektorstartabstand ($d_0$) gleich
| $ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $ |
und die Position des Reflektors relativ zum Sender ist
| $ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $ |
als Funktion von der Zeit vom Beginn der Ablaufverfolgung ($t$).
ID:(11871, 0)
Strahler und Reflektor in Bewegung
Konzept
Im Fall, dass der Emitter mit einer Geschwindigkeit von die Emittergeschwindigkeit ($v_e$) und der Reflektor mit einer Geschwindigkeit von die Reflektor- oder Empfängergeschwindigkeit ($v_o$) sich bewegt, kann der Abstand zwischen Emitter und Reflektor entweder größer ($v_e > v_o$) oder kleiner ($v_e < v_o$) sein. Wenn diese Situation inklusive der Echozeit ($\tau_1$), der Zweite Echozeit ($\tau_2$) und der Zeit zwischen den Impulsen ($\tau$) dargestellt wird, ergibt sich:
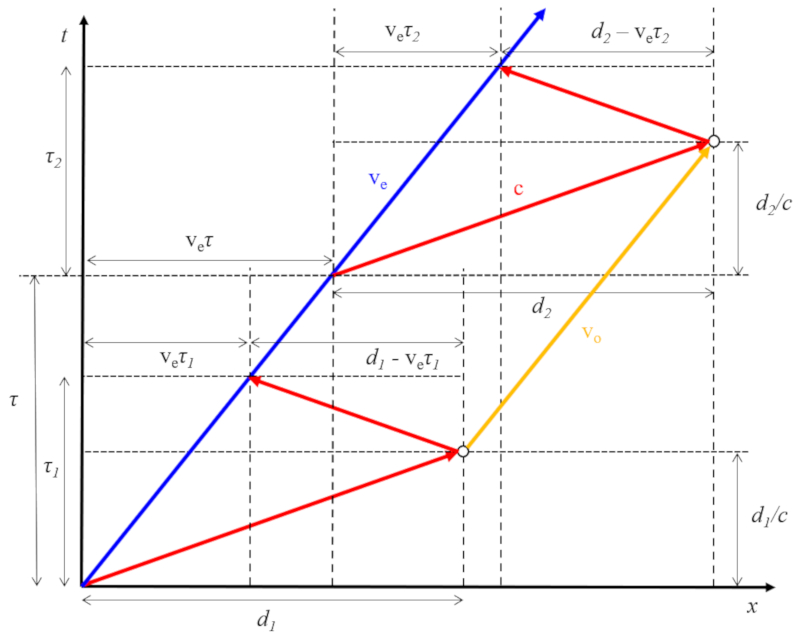
Durch Berechnung des zurückgelegten Weges und der vergangenen Zeit des Reflektors zwischen den beiden Impulsen erhält man die Reflektor- oder Empfängergeschwindigkeit ($v_o$) wie folgt:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
Mit Kenntnis sowohl von die Emittergeschwindigkeit ($v_e$) als auch von die Reflektor- oder Empfängergeschwindigkeit ($v_o$) können wir die Relative position emitter in motion and reflector at rest ($x$) als Funktion von der Zeit vom Beginn der Ablaufverfolgung ($t$) wie folgt angeben:
| $ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$ |
mit die Schallgeschwindigkeit ($c$).
ID:(11872, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ d = \displaystyle\frac{1}{2} c \tau_1 $
d = c * tau_1 /2
$ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $
d_0 =( c + v_e )* tau_1 /2
$ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$
v_o = c *( 2* v_e * tau + ( c + v_e )*( tau_2 - tau_1 ))/(2* c * tau + ( c + v_e )*( tau_2 - tau_1 ))
$ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $
x = ( c + v_e )* tau_1 /2 - v_e * t
$ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$
x =((2* tau * tau_1 +( tau_2 - tau_1 )* t )*( c - v_e )*( v_e + c ))/(( v_e + c )*( tau_2 - tau_1 ) + 2* c * tau ))
ID:(15469, 0)
Emitter- und Reflektorabstand sind in Ruhe
Gleichung
Wenn keine Bewegung vorhanden ist, beträgt die Zeit, die das Signal der Echozeit ($\tau_1$) benötigt, um die Strecke mit der Schallgeschwindigkeit die Schallgeschwindigkeit ($c$) zurückzulegen, $c \tau$, was doppelt so lang ist wie die Entfernung zwischen Sender und Reflektor.
Daher ist die Emitter- und Reflektorabstand sind in Ruhe ($d$):
| $ d = \displaystyle\frac{1}{2} c \tau_1 $ |
ID:(11873, 0)
Beweglicher Emitterabstand und Reflektor in Ruhe
Gleichung
Im Fall, dass der Sender mit einer Geschwindigkeit von die Emittergeschwindigkeit ($v_e$) bewegt wird und der Reflektor sich nicht bewegt, kann seine anfängliche Entfernung die Reflektorstartabstand ($d_0$) anhand der Echozeit der Echozeit ($\tau_1$) geschätzt werden. In diesem Szenario entspricht die zurückgelegte Strecke $c \tau_1$, was der anfänglichen Entfernung zwischen Sender und Reflektor die Reflektorstartabstand ($d_0$) entspricht, und der Rückkehr, die gleich $d_0$ minus der vom Sender zurückgelegten Strecke $v_e\tau_1$. Daher haben wir:
$d_0 + d_0 - v_e\tau_1 = c\tau_1$
oder dass die Reflektorstartabstand ($d_0$) ist:
| $ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $ |
ID:(11874, 0)
Relative Position Emitter in Bewegung und Reflektor in Ruhe
Gleichung
Um die Relative position emitter in motion and reflector at rest ($x$) zu bestimmen, muss man die Reflektorstartabstand ($d_0$) berücksichtigen und den vom Sender zurückgelegten Weg abziehen. Letzterer wird aus die Emittergeschwindigkeit ($v_e$) und der Zeit vom Beginn der Ablaufverfolgung ($t$) berechnet, was zu folgendem Ergebnis führt:
| $ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $ |
ID:(11876, 0)
Reflektorgeschwindigkeit bewegen
Gleichung
Die Reflektor- oder Empfängergeschwindigkeit ($v_o$) kann aus die Emittergeschwindigkeit ($v_e$) und die Schallgeschwindigkeit ($c$) sowie der Echozeit ($\tau_1$), der Zweite Echozeit ($\tau_2$) und der Zeit zwischen den Impulsen ($\tau$) berechnet werden, indem man folgende Formel verwendet:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
Mit die Abstand zum Objekt beim Aussenden des ersten Signals ($d_1$) und die Schallgeschwindigkeit ($c$) lässt sich die Zeit abschätzen, zu der das erste Signal als $d_1/c$ reflektiert wird, und mit die Abstand zum Objekt beim Aussenden des zweiten Signals ($d_2$) der zweite Zeitpunkt als $\tau + d_2/c$. Daher beträgt die Zeit zwischen den Reflexionen der beiden Signale:
$\Delta\tau = \tau + \displaystyle\frac{ d_2 }{ c } - \displaystyle\frac{ d_1 }{ c }$
Die Position, an der das Signal zum ersten Mal reflektiert wird, ist die Abstand zum Objekt beim Aussenden des ersten Signals ($d_1$), und die zweite Position ist ($$). Somit beträgt die zurückgelegte Strecke des Reflektors:
$ \Delta x = v_e \tau + d_2 - d_1 $
Daher beträgt die Geschwindigkeit des Reflektors:
$v_o=\displaystyle\frac{\Delta x}{\Delta t}=\displaystyle\frac{ v_e\tau + d_2 - d_1}{ \tau + \displaystyle\frac{d_2}{c} - \displaystyle\frac{d_1}{c}}$
Wie bereits erwähnt in echozeit $s$, emittergeschwindigkeit $m/s$, reflektorstartabstand $m$ und schallgeschwindigkeit $m/s$, beträgt die Differenz zwischen den zurückgelegten Strecken:
$d_2-d_1=\displaystyle\frac{1}{2}( c + v_e )( \tau_2 - \tau_1 )$
und die resultierende Geschwindigkeit ist:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
ID:(11877, 0)
Beweglicher Abstand zwischen Emitter und Reflektor
Gleichung
Para calcular la posición relativa entre emisor y reflector se debe describir primero la posición del reflector y luego restar la del emisor. Este ultimo se mueve a una velocidad
$d_1 + v_o\left(t - \displaystyle\frac{d_1}{c}\right) = v_ot + d_1\left(1 -\displaystyle\frac{v_o}{c}\right)=v_ot + \left(1 -\displaystyle\frac{v_o}{c}\right)\left(1 +\displaystyle\frac{v_e}{c}\right)c\tau_1$
Como el emisor reduce la distancia en el tiempo según
$v_et$
se tiene que la distancia efectiva entre objeto y emisor es con
| $ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$ |
ID:(11875, 0)