Utilizador: 
Sonar
Storyboard 
Outro uso do som na água são os sonares, tanto como ferramenta tecnológica quanto como técnica utilizada por baleias e golfinhos (biossonares) para determinar distâncias.
Os biossonares são empregados tanto para navegar quanto para caçar, estimando distâncias e até mesmo velocidades para prever o movimento que a presa terá no futuro.
ID:(1597, 0)
Emissor e refletor estão em repouso
Conceito
No caso em que tanto o emissor quanto o refletor não se deslocam, o caminho percorrido pelo som é igual a duas vezes ($$):
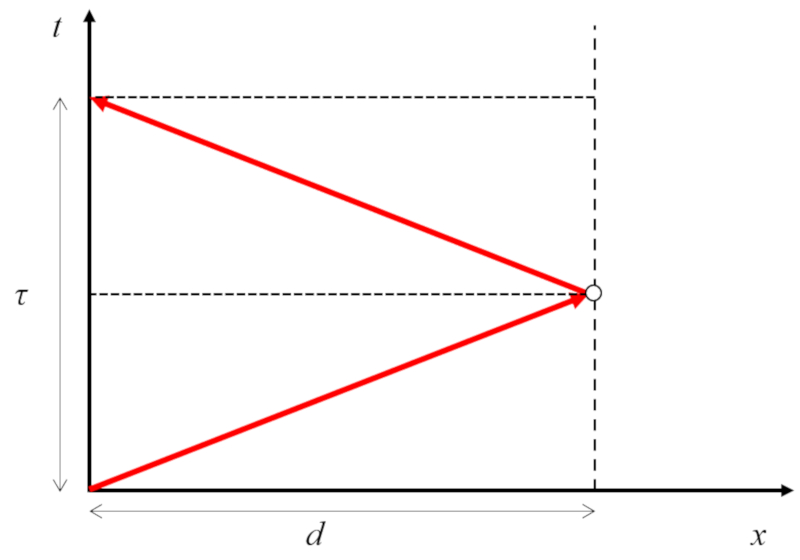
Como a distância é percorrida a la velocidade do som ($c$) em la tempo de eco ($\tau_1$), temos que ($$) é:
| $ d = \displaystyle\frac{1}{2} c \tau_1 $ |
ID:(11870, 0)
Emissor em movimento e refletor em repouso
Conceito
No caso em que o emissor se move a uma velocidade la velocidade do emissor ($v_e$) e o refletor está em repouso, la velocidade do som ($d_0$) varia dependendo se o som que viaja com la velocidade do som ($c$) requer la tempo de eco ($\tau_1$) seja maior (se os corpos se afastam) ou menor (se os corpos se aproximam):
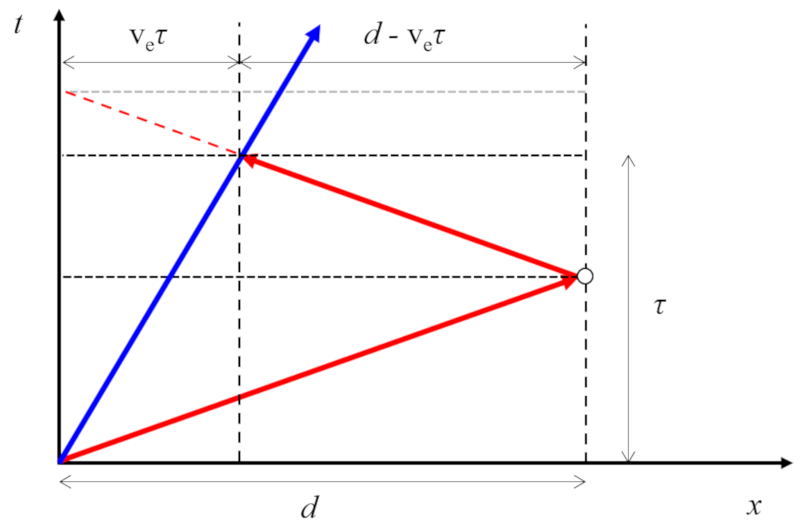
Portanto, la velocidade do som ($d_0$) é igual a
| $ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $ |
e a posição do refletor em relação ao emissor é
| $ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $ |
como função de o tempo desde o início do rastreamento ($t$).
ID:(11871, 0)
Emissor e refletor em movimento
Conceito
En el caso de que el emisor se mueva a una velocidad la velocidade do emissor ($v_e$) y el reflector se desplace a una velocidad la velocidade do refletor ou receptor ($v_o$), la distancia entre el emisor y el reflector puede ser mayor ($v_e > v_o$) o menor ($v_e < v_o$). Si representamos esta situación incluyendo la tempo de eco ($\tau_1$), o segundo tempo de eco ($\tau_2$) y o tempo entre pulsos ($\tau$), obtenemos:
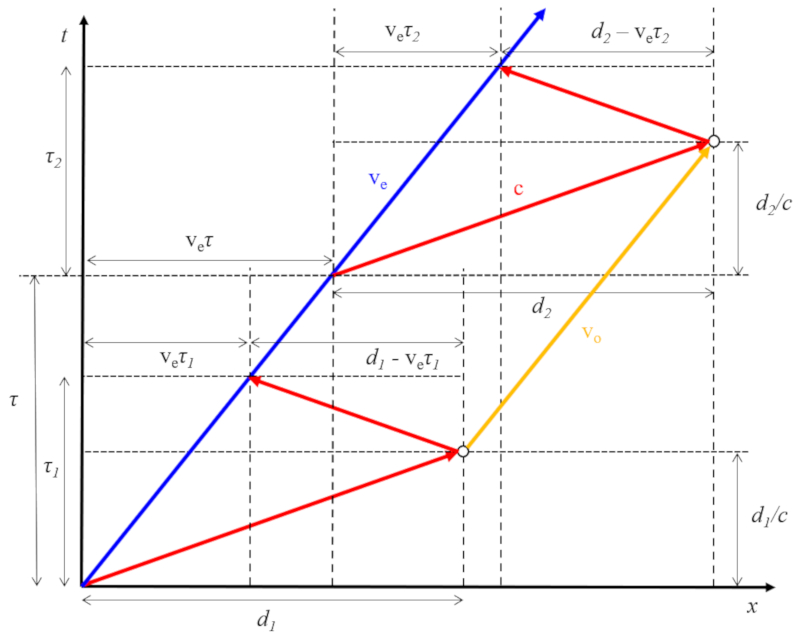
Al calcular el camino recorrido y el tiempo transcurrido por el reflector entre ambos pulsos, se obtiene la velocidade do refletor ou receptor ($v_o$) como:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
Conocidos tanto la velocidade do emissor ($v_e$) como la velocidade do refletor ou receptor ($v_o$), podemos expresar la posição relativa do emissor em movimento e do refletor em repouso ($x$) en función de o tempo desde o início do rastreamento ($t$) de la siguiente manera:
| $ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$ |
con la velocidade do som ($c$).
ID:(11872, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ d = \displaystyle\frac{1}{2} c \tau_1 $
d = c * tau_1 /2
$ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $
d_0 =( c + v_e )* tau_1 /2
$ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$
v_o = c *( 2* v_e * tau + ( c + v_e )*( tau_2 - tau_1 ))/(2* c * tau + ( c + v_e )*( tau_2 - tau_1 ))
$ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $
x = ( c + v_e )* tau_1 /2 - v_e * t
$ x =\displaystyle\frac{(2 \tau \tau_1 +( \tau_2 - \tau_1 ) t )( c - v_e )( v_e + c )}{( v_e + c )( \tau_2 - \tau_1 )+2 c \tau )}$
x =((2* tau * tau_1 +( tau_2 - tau_1 )* t )*( c - v_e )*( v_e + c ))/(( v_e + c )*( tau_2 - tau_1 ) + 2* c * tau ))
ID:(15469, 0)
O emissor de distância e o refletor estão em repouso
Equação
Se não houver movimento, o tempo necessário para o sinal la tempo de eco ($\tau_1$) percorrer a velocidade do som la velocidade do som ($c$) é $c \tau$, o que é o dobro da distância entre o emissor e o refletor.
Portanto, ($$) é:
| $ d = \displaystyle\frac{1}{2} c \tau_1 $ |
ID:(11873, 0)
Distância entre o emissor em movimento e o refletor em repouso
Equação
No caso em que o emissor se desloca a uma velocidade de la velocidade do emissor ($v_e$) e o refletor não se move, sua distância inicial la velocidade do som ($d_0$) pode ser estimada usando o tempo de eco la tempo de eco ($\tau_1$). Neste cenário, a distância percorrida é igual a $c \tau_1$, que é igual à distância inicial entre o emissor e o refletor la velocidade do som ($d_0$), mais o retorno, que é o mesmo $d_0$ menos a distância percorrida pelo emissor $v_e\tau_1$. Portanto, temos:
$d_0 + d_0 - v_e\tau_1 = c\tau_1$
ou que la velocidade do som ($d_0$) é:
| $ d_0 = \displaystyle\frac{1}{2} (c + v_e) \tau_1 $ |
ID:(11874, 0)
Posição relativa do emissor em movimento e do refletor em repouso
Equação
Para determinar la posição relativa do emissor em movimento e do refletor em repouso ($x$), é necessário considerar la velocidade do som ($d_0$) e subtrair o caminho percorrido pelo emissor. Este último é calculado a partir de la velocidade do emissor ($v_e$) e o tempo desde o início do rastreamento ($t$), resultando em:
| $ x = \displaystyle\frac{1}{2}( c + v_e ) \tau_1 - v_e t $ |
ID:(11876, 0)
Velocidade do refletor móvel
Equação
La velocidade do refletor ou receptor ($v_o$) pode ser calculado a partir de la velocidade do emissor ($v_e$) e la velocidade do som ($c$), juntamente com la tempo de eco ($\tau_1$), o segundo tempo de eco ($\tau_2$) e o tempo entre pulsos ($\tau$), utilizando a fórmula:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
Com la distância até o objeto ao emitir o primeiro sinal ($d_1$) e la velocidade do som ($c$), pode-se estimar o tempo em que o primeiro sinal se reflete como $d_1/c$, e com la distância até o objeto ao emitir o primeiro sinal ($d_2$), o segundo tempo como $\tau + d_2/c$. Portanto, o tempo entre os reflexos dos dois sinais é dado por:
$\Delta\tau = \tau + \displaystyle\frac{ d_2 }{ c } - \displaystyle\frac{ d_1 }{ c }$
A posição em que a primeira reflexão do sinal ocorre é La distância até o objeto ao emitir o primeiro sinal ($d_1$), e a segunda é ($$). Portanto, a distância percorrida pelo refletor é dada por:
$ \Delta x = v_e \tau + d_2 - d_1 $
Assim, a velocidade do refletor é:
$v_o=\displaystyle\frac{\Delta x}{\Delta t}=\displaystyle\frac{ v_e\tau + d_2 - d_1}{ \tau + \displaystyle\frac{d_2}{c} - \displaystyle\frac{d_1}{c}}$
Como mencionado anteriormente em tempo de eco $s$, velocidade do emissor $m/s$, velocidade do som $m$ e velocidade do som $m/s$, a diferença entre as distâncias percorridas é dada por:
$d_2-d_1=\displaystyle\frac{1}{2}( c + v_e )( \tau_2 - \tau_1 )$
e a velocidade resulta em:
| $ v_o = \displaystyle\frac{2 v_e \tau + ( c + v_e )( \tau_2 - \tau_1 )}{2 c \tau + ( c + v_e )( \tau_2 - \tau_1 )}c$ |
ID:(11877, 0)