Usuario:
Propagación del sonido
Storyboard 
La propagación de sonido en el océano considera tanto la reflexión en superficie como fondo oceánico y las refracciones que se dan por variaciones en presión, temperatura y salinidad.
ID:(1550, 0)
Interpretación de la refracción del sonido
Concepto
Si observamos cómo varía el sonido con la profundidad y la forma en que se propaga:
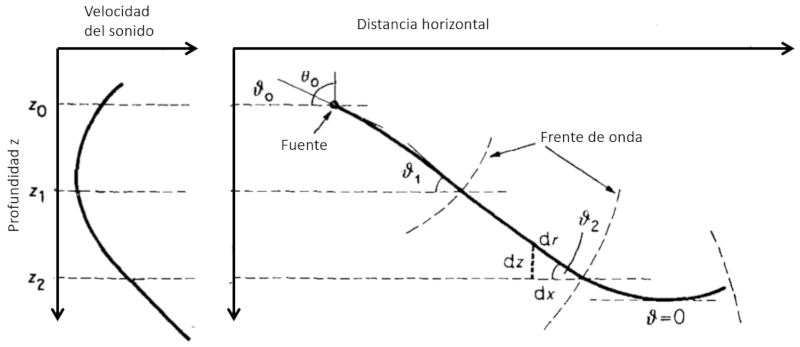
podemos ver que:
• Si la velocidad del sonido aumenta con la profundidad, el ángulo entre el haz y el horizonte tiende a reducirse. Esto significa que el sonido tenderá a disminuir su descenso hasta el punto en que se vuelva horizontal y, por simetría, continuará ascendiendo hacia la superficie.
• Si la velocidad del sonido disminuye con la profundidad, el ángulo entre el haz y el horizonte tiende a aumentar. Esto significa que el sonido tenderá a aumentar su descenso en dirección al fondo.
ID:(11804, 0)
Caso la velocidad del sonido se incrementa
Concepto
Sonido emitido en una profundidad en que la velocidad del sonido aumenta con la profundidad los haces terminan volviendo a la superficie donde se reflejan y vuelven a penetrar el medio:
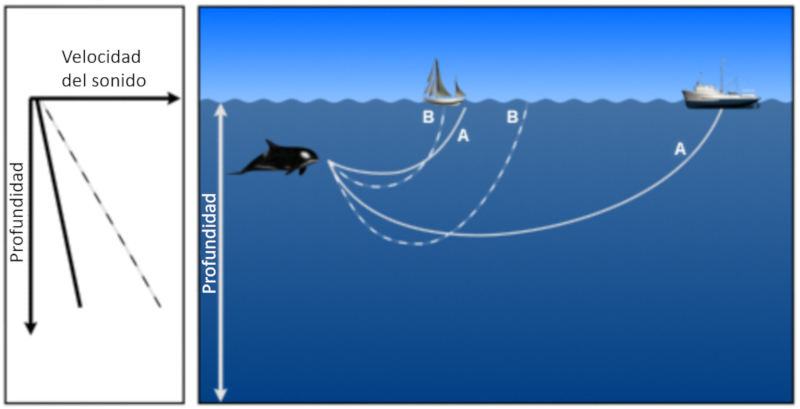
ID:(11805, 0)
Caso la velocidad del sonido se incrementa y luego se reduce
Concepto
Sonido emitido en una profundidad en que la velocidad del sonido aumenta con la profundidad los haces terminan volviendo a la superficie. Sin embargo si a partir de un punto la velocidad del sonido se reduce se observa que haces con mayor angulo son refractado hacia las profundidades:
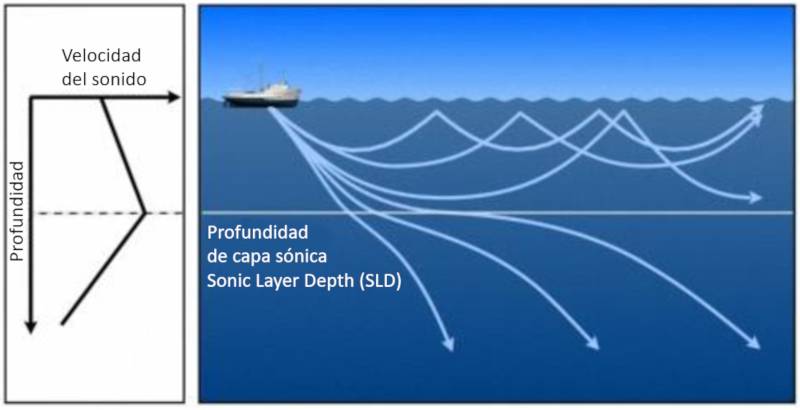
Se forma asi una zona en que los haces vuelven a la superficie. Dicha profundidad se denomina profundidad de capa sónica SLD (Sonic Layer Depth).
ID:(11806, 0)
Canal de sonido
Concepto
Cuando el sonido se reduce y luego vuelve a incrementarse, se forma una zona donde tiende a regresar a la velocidad mínima. Esta área se conoce como el canal del sonido y se extiende desde la profundidad de la capa sónica (SLD) hasta una profundidad conjugada:
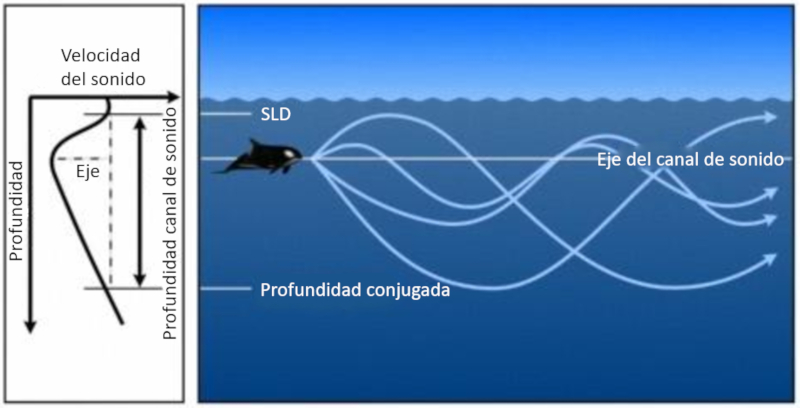
La profundidad en la que la velocidad del sonido alcanza un mínimo se denomina el eje del canal del sonido.
Tanto la propagación en la zona superior a la profundidad de la capa sónica (SLD) como en el canal del sonido existen. Sin embargo, la primera zona presenta el problema de que la superficie amortigua el sonido, por lo que el canal del sonido termina siendo más efectivo.
ID:(11807, 0)
Pérdida del sonido en la capa superior
Concepto
Las ondas sonoras que se propagan sobre la profundidad de capa sónica puede filtrar a la zona inferior:
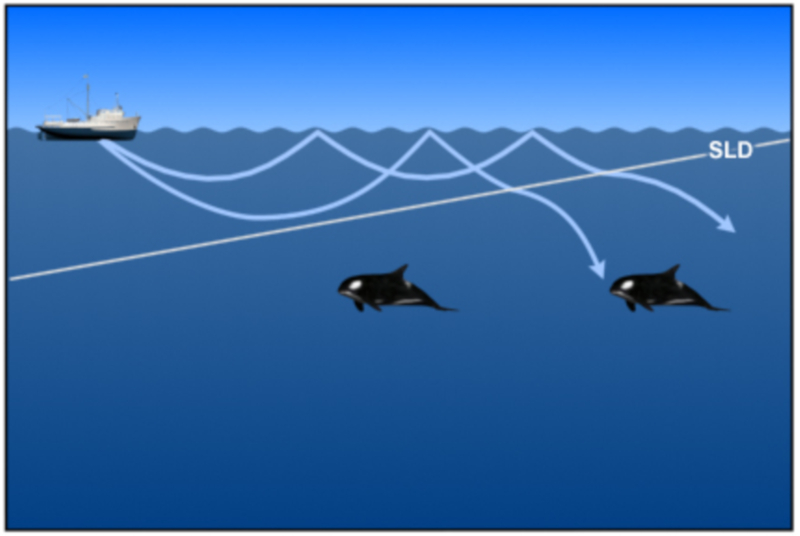
ID:(11808, 0)
Caso poca profundidad con velocidad del sonido que se incrementa
Concepto
Si el agua es poco profunda y la velocidad del sonido solo aumenta con la profundidad, entonces el sonido regresa a la superficie ya sea por refracción o por reflexión en el fondo, para luego reflejarse en la superficie:
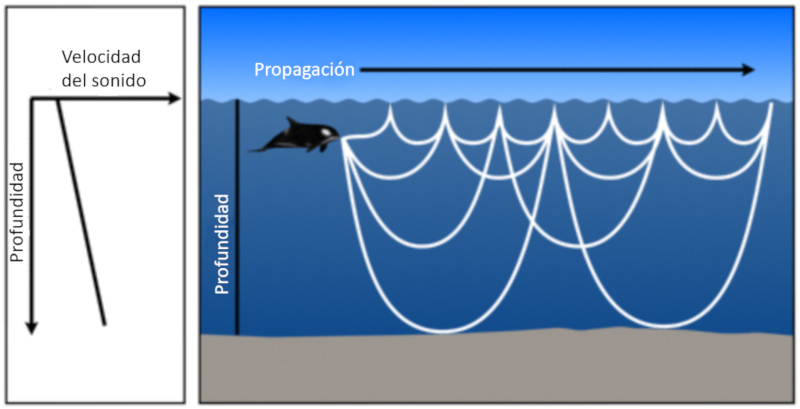
ID:(11809, 0)
Caso poca profundidad con velocidad del sonido que se reduce
Concepto
Si el agua es poco profunda y la velocidad del sonido solo se reduce con la profundad se tiene que el sonido tiende a ir hacia el fondo donde se refleja:
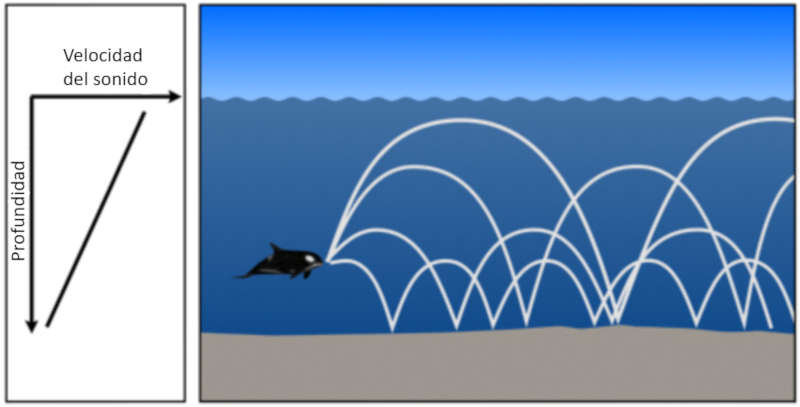
ID:(11810, 0)
Perfil de la temperatura y velocidad del sonido
Concepto
La temperatura atraviesa una zona donde es aproximadamente constante antes de descender. Permanece constante en la primera zona debido a las turbulencias generadas por el viento, que tienden a mezclar el agua.
La curva de la velocidad del sonido muestra que alcanza un máximo que define la profundidad de la capa sónica. En su punto máximo se define la profundidad de la capa sónica:
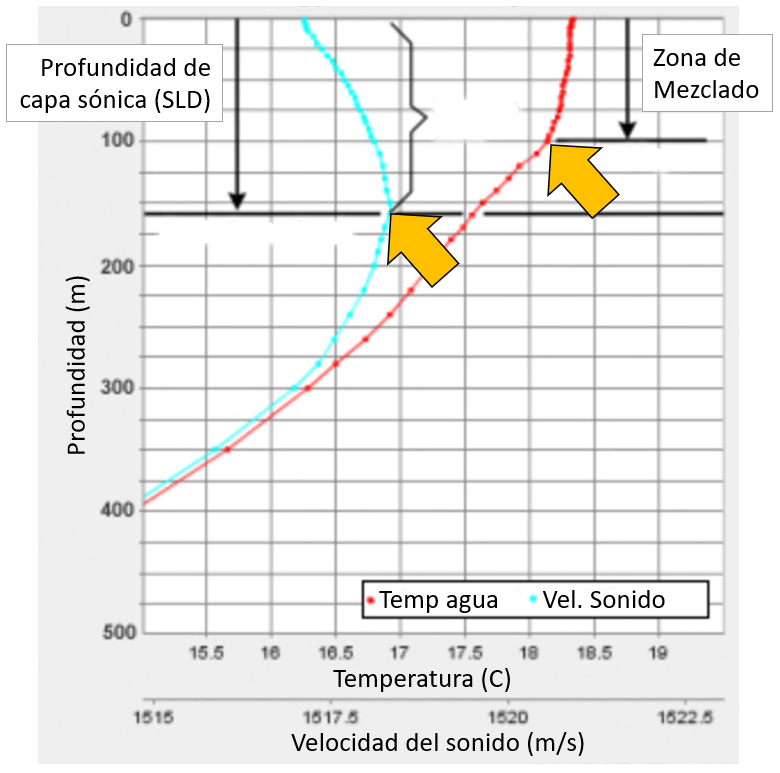
ID:(11811, 0)
Comportamiento en mayor profundidad
Concepto
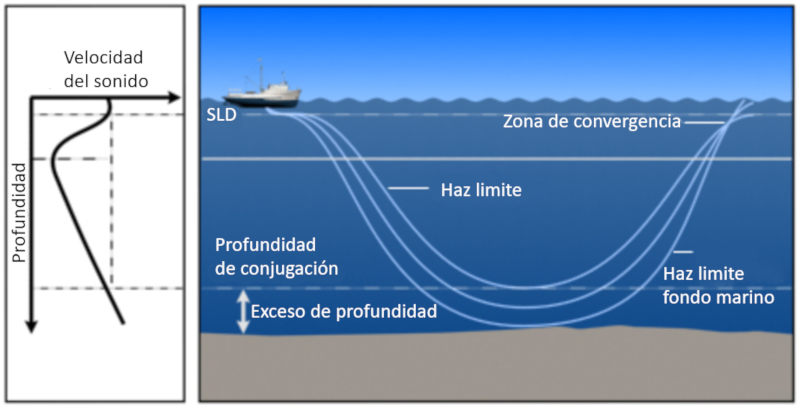
En general, debido a la gravedad, la velocidad del sonido siempre aumenta con la profundidad. Cuando un haz de sonido alcanza la profundidad de la capa sónica SLD, eventualmente se desvía y regresa a la superficie. Los haces que logran regresar a la superficie se sitúan entre un límite definido por la reflexión en el fondo y el límite del haz que logra penetrar en las capas inferiores y finalmente alcanza la superficie.
ID:(11812, 0)
Propagación a distancias mayores
Concepto
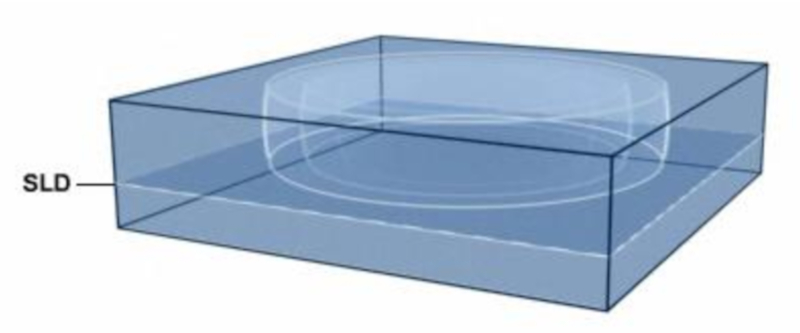
Para el sonido emitido cerca de la superficie, la propagación puede modelarse como una propagación esférica. El sonido de alta frecuencia tiende a amortiguarse a distancias mayores, por lo que el modelo esférico es adecuado. Sin embargo, para el sonido de baja frecuencia, puede viajar a lo largo de toda la cuenca. En este caso, se desplaza a través de la zona superior a la profundidad de la capa acústica (SLD) y/o a través del canal de sonido. En ambos casos, el sistema puede modelarse con coordenadas cilíndricas:
ID:(11813, 0)
Perfil real de sonido
Concepto
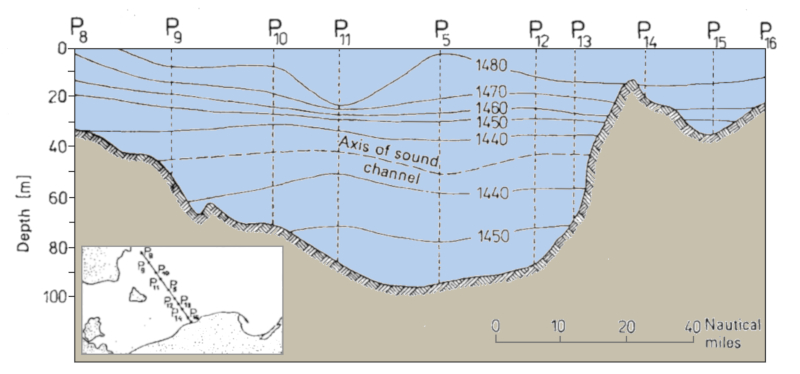
Se puede obtener un perfil de una zona, como por ejemplo un canal, donde se representan las velocidades para cada profundidad. De esta manera, se pueden detectar los canales de sonido y la profundidad de la capa sonora:
ID:(11826, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ I =\displaystyle\frac{ P }{ 2 \pi r h }$
I = P /(2* pi * r * h )
$\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$
sin( theta_i )/sin( theta_r )= c_i / c_e
$\displaystyle\frac{ d\vartheta }{ dz }=-\displaystyle\frac{\tan \vartheta }{ c } \displaystyle\frac{ dc }{ dz }$
diff( vartheta , z )=-tan( vartheta )*diff( c , z )/ c
ID:(15466, 0)
Ley de Snell en función de la velocidad
Ecuación
La relación entre los ángulos de incidencia y refractados indicados en la siguiente gráfica
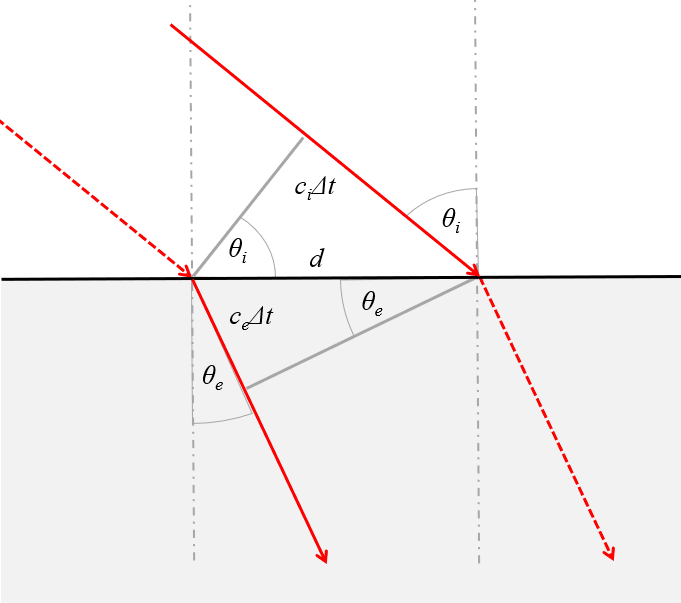
se pueden escribir en función de la velocidad de la luz en cada medio
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
| $\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }$ |
ID:(3342, 0)
Refracción del sonido
Ecuación
La refracción del sonido al pasar de un medio a otro está generalmente descrita por la ley de Snell:
$\displaystyle\frac{\sin\theta_2}{\sin\theta_1}=\displaystyle\frac{c_2}{c_1}$
donde el ángulo $\theta$ es el ángulo de incidencia entre la normal a la superficie y el haz, y $c$ son las velocidades del sonido en los medios 1 y 2. En el caso de un haz propagándose a través del agua del océano, las velocidades cambian gradualmente. Por otro lado, es conveniente trabajar con un ángulo $\vartheta$ del haz con respecto a la horizontal. Por lo tanto, la ley puede ser reescrita reemplazando el seno del ángulo $\theta$ por el coseno del ángulo complementario $\vartheta$. Si consideramos una pequeña variación del ángulo y la velocidad al aumentar la profundidad en $dz$, obtenemos:
$\displaystyle\frac{\cos(\vartheta + d\vartheta)}{\cos\vartheta}\sim 1-\tan\vartheta d\vartheta = 1+\displaystyle\frac{dc}{c}$
por lo que la relación por variación de profundidad es:
| $\displaystyle\frac{ d\vartheta }{ dz }=-\displaystyle\frac{\tan \vartheta }{ c } \displaystyle\frac{ dc }{ dz }$ |
ID:(11803, 0)
Propagación del sonido en el canal sonico
Ecuación
Mientras que en el espacio el sonido se propaga en todas las direcciones reduciéndose la intensidad con la distancia al inverso del radio al cuadrado
| $ I =\displaystyle\frac{1}{4 \pi }\displaystyle\frac{ W }{ r ^2}$ |
dentro del canal sónico lo hace en un sistema bidimensional con lo que la intensidad se reduce con la distancia a la inversa con :
| $ I =\displaystyle\frac{ P }{ 2 \pi r h }$ |
ID:(11878, 0)