Benützer: 
Schallgeschwindigkeit im Meer
Storyboard 
Die Schallgeschwindigkeit im Meer hängt von Druck, Temperatur und Salzgehalt ab.
ID:(1548, 0)
Schallgeschwindigkeit mit Tiefe
Konzept
Die Schallgeschwindigkeit im Ozean variiert mit der Tiefe, wie in der Grafik dargestellt:
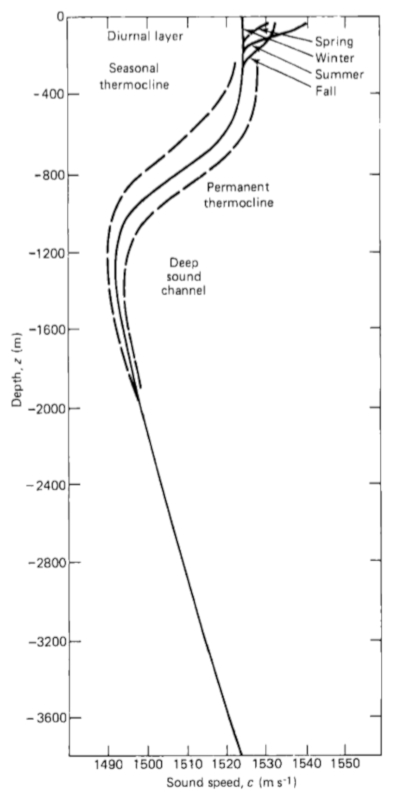
Die Form der Kurve kann je nach Jahreszeit variieren.
ID:(11814, 0)
Abhängigkeit von der Schallgeschwindigkeit
Konzept
Die Schallgeschwindigkeit im Ozean hängt von Temperatur und Druck ab, wie in der Grafik dargestellt:
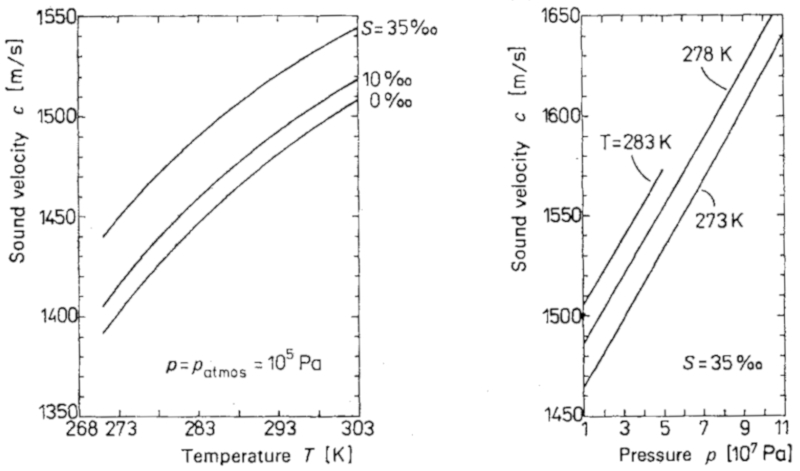
ID:(11815, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
c = c_0 T ^3- c_1 T ^2+( c_3 - c_2 s ) T + c_4 p + c_5 s - c_6
c = c_0 * T ^3- c_1 * T ^2+( c_3 - c_2 * s )* T + c_4 * p +c_5 * s - c_6
\displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e }
sin( theta_i )/sin( theta_r )= c_i / c_e
ID:(15465, 0)
Ley de Snell en función de la velocidad
Gleichung
La relación entre los ángulos de incidencia y refractados indicados en la siguiente gráfica
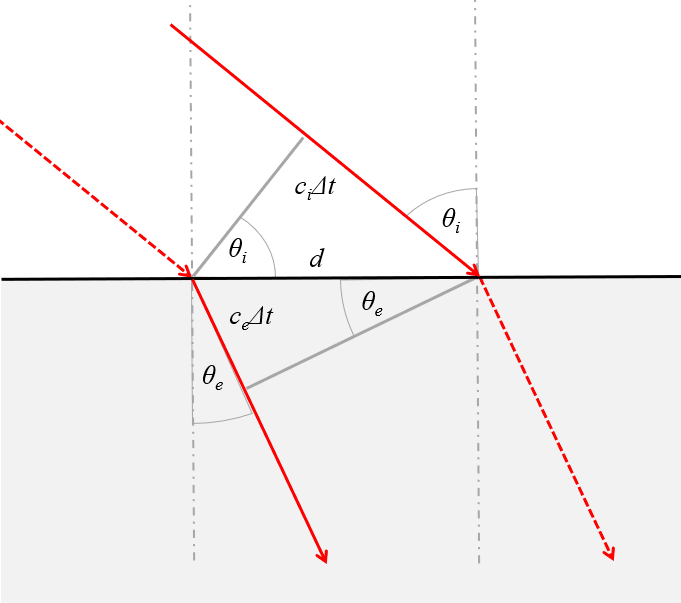
se pueden escribir en función de la velocidad de la luz en cada medio
| \displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e } |
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}
y\\n\\n
\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}
\\n\\nSi se despeja en ambas ecuaciones la distancia
d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}
por lo que se tiene que
| \displaystyle\frac{ \sin\theta_i }{\sin \theta_r }=\displaystyle\frac{ c_i }{ c_e } |
ID:(3342, 0)
Schallgeschwindigkeitsgleichung
Gleichung
Im Jahr 1977 entwickelten Clay und Medwin ein Modell zur Schätzung der Schallgeschwindigkeit in Abhängigkeit von Temperatur, Salinität und Druck.
die Schallgeschwindigkeit (c) kann basierend auf die Presión hidrostatica (p), die Temperatur (T) und die Salzgehalt (s) mit folgendem Ausdruck geschätzt werden:
| c = c_0 T ^3- c_1 T ^2+( c_3 - c_2 s ) T + c_4 p + c_5 s - c_6 |
wobei c_i empirische Konstanten sind.
Referenz: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah und Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, Nr. 22, November 2017.
ID:(11816, 0)