Benützer:
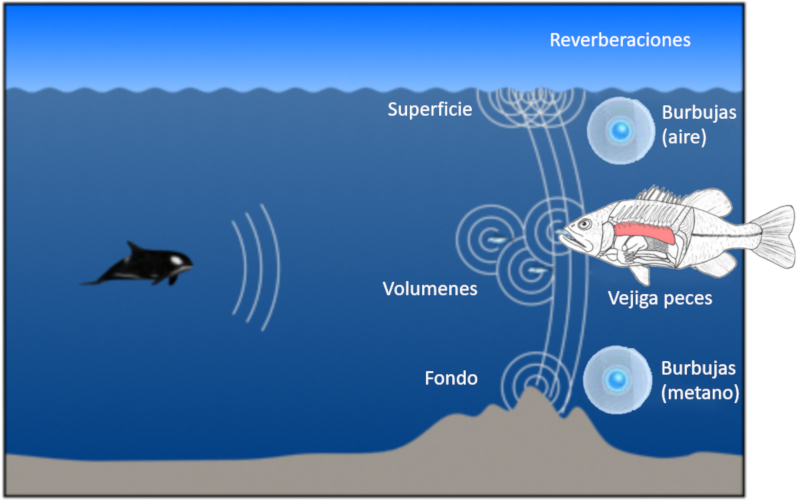
Absorption, Dispersion und Schallquellen
Storyboard 
Die Dämpfung von Schallwellen im Ozean hängt von der Frequenz des Schalls ab. Für niedrige Frequenzen (unter 10 kHz) stammt der Hauptbeitrag von Borsäureionen, während im Bereich zwischen 10 kHz und 100 kHz der Effekt von Magnesiumsulfationen eine Rolle spielt. Für höhere Frequenzen ist die Dämpfung hauptsächlich auf die Viskosität des Wassers zurückzuführen.
ID:(1549, 0)
Bodenstörung
Bild
Steigungen im Hintergrund führen zu Störungen der Schallausbreitung:
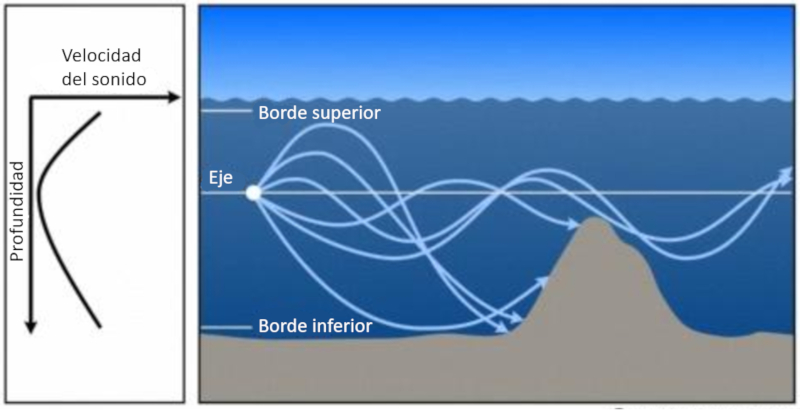
ID:(11824, 0)
Schallerzeugung
Bild
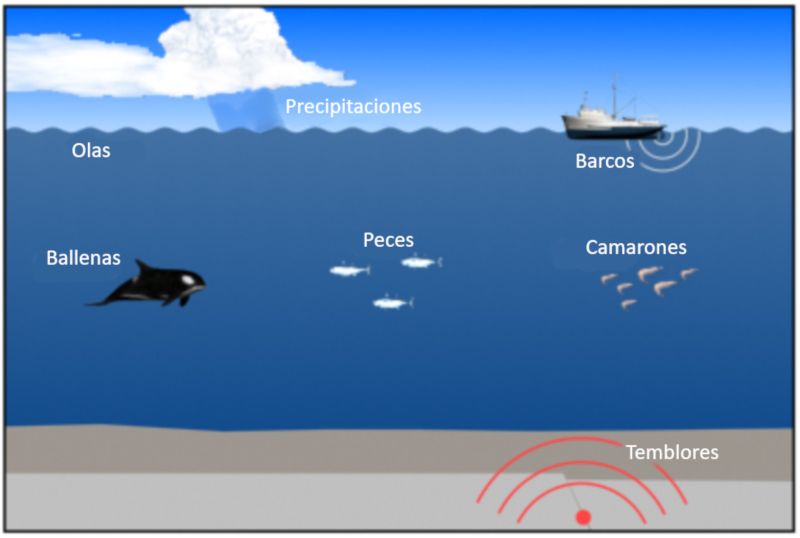
In den Ozeanen gibt es verschiedene Schallquellen. Unter ihnen sind
• Menschliche Quellen (vor allem Schiffe)
• Regen an der Oberfläche
• Fisch, Garnelen, Wale usw.
• Wellen
• Erdbeben
ID:(11825, 0)
Ton und seine Frequenz
Bild
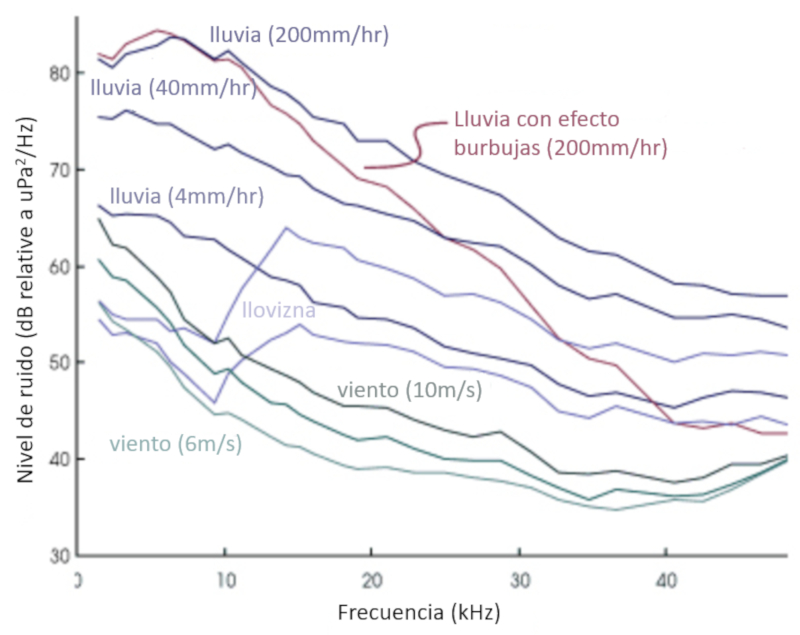
Die Spektren der Quellen, die der Messung der Schallamplituden nach ihrer Frequenz entsprechen, zeigen das starke Vorhandensein der Regenfälle:
ID:(11827, 0)
Schalldämpfung
Bild
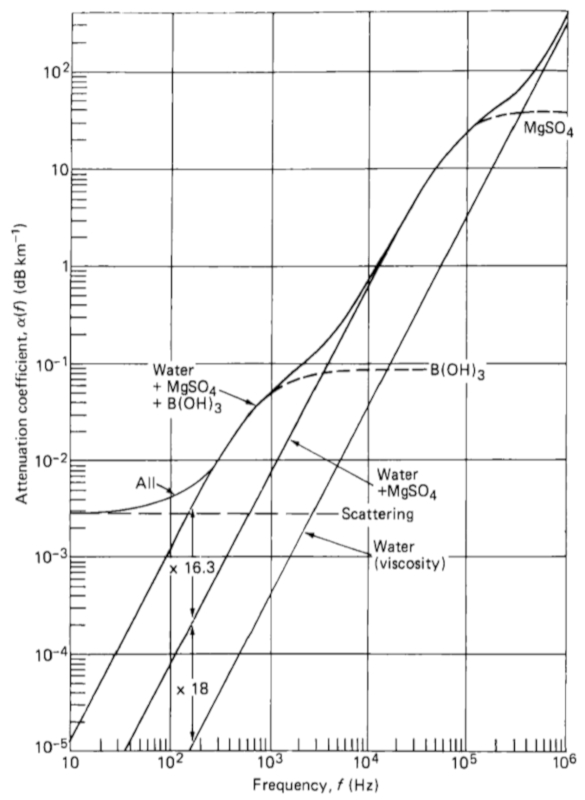
Es gibt drei Mechanismen, die den Schall im Meer dämpfen:
• Magnesiumsulfationen-Relaxationen (bis zu 10 kHz)
• Borsäureionenrelaxationen (bis zu 100 kHz)
• Wasserviskosität (bei allen Frequenzen)
ID:(11823, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \alpha = \alpha_1 \displaystyle\frac{ \nu ^2}{ \nu ^2+\nu_1^2} + \alpha_2 \displaystyle\frac{ \nu ^2}{ \nu ^2+ \nu_2 ^2} + \alpha_2 \nu ^2 + \alpha_0 $
alpha = alpha_1 * nu ^2/( nu ^2+ nu_1 ^2) + alpha_2 * nu ^2/( nu ^2+ nu_2 ^2) + alpha_2 * nu ^2 + alpha_0
$ I = I_0 e^{ - \alpha r }$
I = I_0 * exp(- alpha * r )
ID:(15467, 0)
Schallabsorptionseffekt
Gleichung
El factor de absorción indica como la energía se va perdido a lo largo del camino recorrido. Como la perdida es siempre proporcional a la intensidad existente se tiene un decaimiento exponencial.
Por ello con
| $ I = I_0 e^{ - \alpha r }$ |
ID:(11834, 0)
Entspannungsprozesse im Meerwasser
Gleichung
Existe una amortiguación del sonido en agua de mar por efecto de interacción de moléculas con los iones de hidróxido (OH-) o con moléculas de agua. Esto se denomina procesos de relajación y ocurren en el agua de mar principalmente con:
• moléculas de agua entre estas
• ácido bórico que interactua con los iones de hidróxido $OH^-$s: $B(OH)_3\cdot OH^- \rightleftharpoons B(OH)_4$
• sulfato de magnesio que interactua con moléculas de agua $H_2O$: $MgSO_4 + 2nH_2O \rightleftharpoons Mg^{2+}nH_2O + SO_4^{-2}nH_2O$
Los tiempos de relajamiento y sus frecuencias son del orden de
| Componente | Tiempo de relajamiento | Frecuencia |
| Agua | $10^{-11}s$ | $10^5,MHz$ |
| Ácido bórico | $10^{-3}s$ | $1,kHz$ |
| Sulfato de magnesio (1) | $10^{-5}s$ | $100,kHz$ |
| Sulfato de magnesio (2) | $2\times 10^{-8}s$ | $200,kHz$ |
Sobre esta base se estima el factor de absorción en función de la frecuencia y suponiendo pH típico es con :
| $ \alpha = \alpha_1 \displaystyle\frac{ \nu ^2}{ \nu ^2+\nu_1^2} + \alpha_2 \displaystyle\frac{ \nu ^2}{ \nu ^2+ \nu_2 ^2} + \alpha_2 \nu ^2 + \alpha_0 $ |
En este caso el primer termino es el que depende del ácido bórico, el segundo del sulfato de magnesio y el tercero de la ionización propia del agua. Ademas se puede comentar que no existe un efecto por la salinidad (no hay relajación por iones de sodio y/o cloro).
Mas detalles en el articulo Study of Absorption Loss Effects on Acoustic Wave Propagation in Shallow Water using Different empirical Models, Yasin Yousif Al-Aboosil, Mustafa Sami Ahmed, Nor Shahida Mohd Shah and Nor Hisham Haji Khamis
ID:(11833, 0)