Usuario:
Intercambio de calor
Storyboard 
El intercambio de calor entre la atmósfera y el océano se refiere al proceso por el cual la atmósfera transfiere o absorbe calor del océano, equilibrando así las temperaturas entre ambos.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1580, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$
delta_c =sqrt( D * rho / eta )* delta_eta
$ \epsilon = \displaystyle\frac{ \eta ^3 }{ \rho ^3 \delta_{\eta} ^4 }$
epsilon = eta ^3/( rho ^3* delta_eta ^4 )
$ H_z = C_H \rho_a c_p ( T_z - T_0 ) U_z $
H_z = C_H *rho_a * c_p * ( T_z - T_0 )* U_z
ID:(15642, 0)
Perfil de temperatura en la capa superficial (MOST)
Ecuación
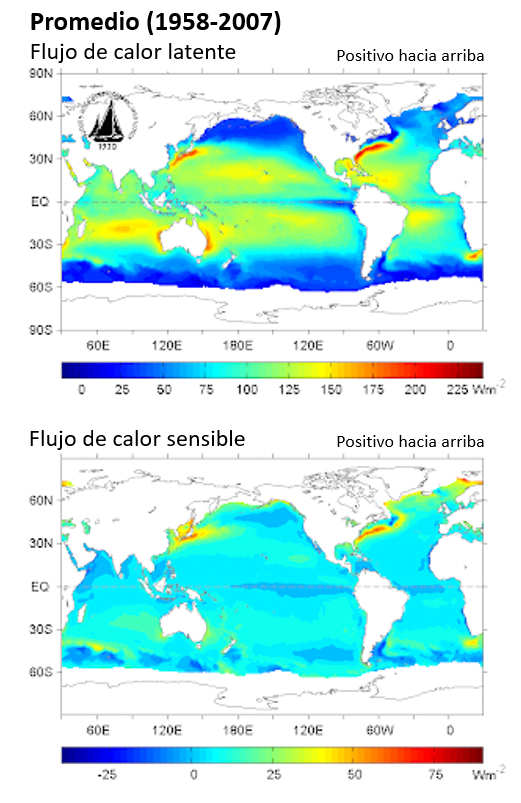
Para el caso del flujo de calor, se debe tener en cuenta el contenido de calor, que se estima utilizando la densidad, el calor específico y la temperatura, así como la velocidad del viento y el coeficiente de transmisión. De esta manera, el flujo de calor se puede expresar como sigue:
| $ H_z = C_H \rho_a c_p ( T_z - T_0 ) U_z $ |
En la teoría de similitud de Monin-Obukhov (MOST), la energía calórica de la superficie, representada por
$\rho_a c_p (T_z - T_0)$
se transfiere al agua mediante el coeficiente de transferencia $C_H$ y la velocidad del aire $U_z$, generando así el flujo de calor.
| $ H_z = C_H \rho_a c_p ( T_z - T_0 ) U_z $ |
ID:(12223, 0)
Disipación de energía en capa superficial
Ecuación
La energía disipada se puede estimar de la viscosidad, densidad y grosor de la capa.
Por ello con es
| $ \epsilon = \displaystyle\frac{ \eta ^3 }{ \rho ^3 \delta_{\eta} ^4 }$ |
None
ID:(12230, 0)
Grosor superficie y capa viscosa
Ecuación
El grosor de la superficie y de la capa viscosas son proposicionales siendo la constante una función de la constante difusión, viscosidad y densidad.
Por ello con es
| $ \delta_c = \sqrt{\displaystyle\frac{ \rho D }{ \eta }} \delta_{\eta}$ |
None
ID:(12229, 0)