Usuario:


Modelo SIR
Storyboard

El modelo SIR considera una enfermedad que infecta personas susceptibles (S) formando infectados (I) que posteriormente se recuperan (R).

>Modelo

ID:(347, 0)


Modelos SIR
Ecuación

>Top, >Modelo


Los modelos tipos SIR consideran tres tipos de poblaciones, los susceptibles S, los infectados I y los recuperados R.

En la medida que

• la infección no es mortal,
• el modelo no incluya natalidad
• el modelo no incluya muerte por otra causa

el numero total de la población sera igual a la suma de los tres grupos:

$N=S+I+R$

ID:(871, 0)


Mecanismo de contagio
Ecuación

>Top, >Modelo


Probabilidad de que una persona que encuentro este infectada es\\n\\n

$\displaystyle\frac{I}{N}$

\\n\\no sea casos favorables I partido por casos posibles N. Normalmente la persona tiene contacto con C personas por lo que se dan \\n\\n

$C\displaystyle\frac{I}{N}$

\\n\\noportunidades de contagiar a un sano. La probabilidad de contagiar va a depender del tiempo que se tiene contacto. Supongamos que consideramos un tiempo dt, en ese caso si la probabilidad por tiempo de contagiar es \beta la probabilidad en el tiempo dt de que un individuo infectado contagie a uno sano es\\n\\n

$\beta dt$

\\n\\nCon ello en el tiempo dt la probabilidad de que una persona sana se infecte es por tiempo dt igual a\\n\\n

$C\displaystyle\frac{I}{N}\beta$

\\n\\nPara obtener el numero total de infectados en el tiempo dt tenemos que considerar que la probabilidad recién calculada afecta a todos los susceptibles de contagio. Por ello el numero de sanos S decrece en un tiempo dt en una cantidad igual a\\n\\n

$C\displaystyle\frac{I}{N}S\beta$



o sea

$i(t)=C\displaystyle\frac{I}{N}S\beta$

ID:(8106, 0)


Mecanismo de contagio - ecuación susceptibles de SIR
Ecuación

>Top, >Modelo


Como el número de susceptibles S se reduce en función de los infectados por tiempo i\\n\\n

$\displaystyle\frac{dS}{dt}=-i(t)$



se tiene que con

$i(t)=C\displaystyle\frac{I}{N}S\beta$



la ecuación para calcular el desarrollo de la población susceptibles es

$\displaystyle\frac{dS}{dt}=-C\displaystyle\frac{I}{N}S\beta$

ID:(4068, 0)


Numero de los que permanecen infectado
Ecuación

>Top, >Modelo


Si para el día t' se contagian i(t') personas, el total de infectados en un día t sera la suma de todos los infectados desde el comienzo la aparición de la enfermedad en un tiempo 0, o sea\\n\\n

$\displaystyle\int_0^tdt'i(t')$



Si deseamos estimar los que aun permanecen infectados debemos restar todos los que a la fecha se han recuperado, los que son R(t). Por ello el numero que aun permanece infectado en el tiempo t es

$I(t)=\displaystyle\int_0^tdtau i(tau)-R(t)$

ID:(3888, 0)


Variación del numero de infectados
Ecuación

>Top, >Modelo


Para conocer la variación en el tiempo del numero de infectados se puede derivar en el tiempo la ecuación

$I(t)=\displaystyle\int_0^tdtau i(tau)-R(t)$



con lo que se obtiene la ecuación

$\displaystyle\frac{dI}{dt}=i(t)-\displaystyle\frac{dR}{dt}$

ID:(4069, 0)


Mecanismo de recuperación/muerte
Ecuación

>Top, >Modelo


La pregunta ahora es como las personas contagiadas (I) se recuperan. En general la recuperación/muerte ocurre a un tiempo medio del contagio. Para modelar se requiere una función probabilista de que la persona se recupere/muera entre un tiempo t y t + dt después de ser contagiado. Si el numero que se contagio entre un tiempo t' y t'+dt es i(t'), los que se recuperan en el tiempo $t$ es igual a la suma de todos los tiempos en que se puede haber contagiado la persona

$r(t)=\displaystyle\int_0^t dtau p(t-tau)i(tau)$

ID:(3889, 0)


Total de recuperados, modelo SIR
Ecuación

>Top, >Modelo


Si el número que se recupera entre los tiempos t' y t'+dt es

$r(t)=\displaystyle\int_0^t dtau p(t-tau)i(tau)$



entonces los recuperados totales al tiempo t serán

$R(t)=\displaystyle\int_0^t dtau r(tau)$

ID:(3890, 0)


Ecuación diferencial de los recuperados
Ecuación

>Top, >Modelo


Como el numero de recuperados es

$R(t)=\displaystyle\int_0^t dtau r(tau)$



y el número diario es

$r(t)=\displaystyle\int_0^t dtau p(t-tau)i(tau)$



la derivada del número de recuperados es igual a

$\displaystyle\frac{dR}{dt}=\int_0^t dtau p(t-tau)i(tau)$

ID:(3891, 0)


Modelo simplificado de recuperación - ecuación recuperados de SIR
Ecuación

>Top, >Modelo


La cantidad de recuperados diarios se calculaba sumando sobre todos los contagiados históricos i(t') ponderados por la probabilidad p de que en el día considerado se terminara el proceso de recuperación:

$r(t)=\displaystyle\int_0^t dtau p(t-tau)i(tau)$



que corresondía a la variación diaria del total de recuperados

$\displaystyle\frac{dR}{dt}=\int_0^t dtau p(t-tau)i(tau)$



Como el numero de infectados diarios es

$i(t)=C\displaystyle\frac{I}{N}S\beta$

\\n\\nse tiene que la variación de recuperados es de la forma:\\n\\n

$\displaystyle\frac{dR}{dt}=\displaystyle\frac{\beta C}{N}\displaystyle\int_0^t dt' p(t-t')S(t')I(t')$

\\n\\nSi los infectados son pocos comparados con los susceptibles y la función probabilidad decae mas rápido de lo que varia el numero de infectados la integral se puede reemplazar por una constante\\n\\n

$\displaystyle\frac{\beta C}{N}\displaystyle\int_0^t dt' p(t-t')S(t')I(t')\sim\left[\displaystyle\frac{\beta C}{N}\displaystyle\int_0^t dt' p(t-t')S(t')\right]I(t)\sim\gamma I(t)$



con lo que la ecuación de recuperación queda como

$\displaystyle\frac{dR}{dt}=\gamma I$

ID:(4072, 0)


Reescribiendo la segunda ecuación SIR

Ecuación

>Top, >Modelo


Si se reemplaza la tercera ecuación del modelo SIR

$\displaystyle\frac{dR}{dt}=\gamma I$



en la segunda

$\displaystyle\frac{dI}{dt}=i(t)-\displaystyle\frac{dR}{dt}$



y empleando

$i(t)=C\displaystyle\frac{I}{N}S\beta$



se obtiene una ecuación en que se puede comprender las situaciones en que la enfermedad propaga o se logra controlar

$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I$

ID:(4073, 0)


Aproximación de Sobrevivientes sin contagio, modelo SIR
Ecuación

>Top, >Modelo


Como vimos existe un limite en que la propia enfermedad auto controla su expansión simplemente por la falta de susceptibles de ser contagiados. La pregunta es de que tamaño es el grupo que se salva de la infección. Si dividimos la ecuación

$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I$



por

$\displaystyle\frac{dS}{dt}=-C\displaystyle\frac{I}{N}S\beta$

\\n\\nse puede obtener una ecuación independiente del tiempo (o de la variable a temporal u) de la forma\\n\\n

$\displaystyle\frac{dI}{dS}=-1+\displaystyle\frac{\gamma}{\beta C}\displaystyle\frac{N}{S}$

\\n\\nSi se integra esta ecuación suponiendo condiciones iniciales S_0 y I_0 se obtiene que\\n\\n

$I - I_0 = (S_0 - S) + \displaystyle\frac{\gamma N}{\beta C}\ln\displaystyle\frac{S}{S_0}$

\\n\\nPara determinar el numero de sobreviviente nos interesa el caso en que ya se estabilizo la situación y ya no tenemos infectados (I = 0). Ademas se puede suponer que los infectados iniciales son algunos pocos es decir I_0\ll S_0\\n\\nCon ello la ecuación para el calculo de sobrevivientes se reduce\\n\\n

$(S_0-S)+\displaystyle\frac{\gamma N}{\beta C}\ln\displaystyle\frac{S}{S_0}=0$



Esta ecuación no se puede resolver en forma exacta, sin embargo si se expande el logaritmo mediante Taylor hasta segundo orden se logra resolver siendo el tamaño de la población no infectada

$S_{\infty}=S_0\left(3-2\displaystyle\displaystyle\frac{\beta C}{\gamma}\displaystyle\displaystyle\frac{S_0}{N}\right)$

ID:(4077, 0)


Susceptibles críticos
Ecuación

>Top, >Modelo


Inicialmente se puede considerar que S es similar a N con lo que el sistema comienza a propagarse fuera de control si en

$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I$

\\n\\nel factor\\n\\n

$\displaystyle\frac{C\beta}{\gamma}\displaystyle\frac{S}{N}-1 > 0$

\\n\\nes positivo. Esto ocurre si el factor\\n\\n

$\displaystyle\frac{C\beta}{\gamma}\displaystyle\frac{S}{N}$

\\n\\nes mayor que uno. Como inicialmente la población susceptible S es similar a toda la población considerada N se tiene que el sistema se propaga fuera de control si se da que:\\n \\n

$\displaystyle\frac{C\beta}{\gamma} > 0$



Por otro lado con el tiempo la propia enfermedad reducirá el número de susceptibles haciendo que esta se autocontrola por efecto de la reducción de nuevas victimas. Estas situación se dará si el número de susceptibles llega a

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{\gamma}{C\beta}$

que corresponde a la situación en que la curva de infectados alcanza su máximo. Es decir el número de susceptibles críticos es el numero de susceptibles que van quedando al momento que el número de infectados alcanza su máximo.

El número de susceptibles críticos muestra que la vacunación preventiva ayuda a controlar la enfermedad creando una situación en que los susceptibles iniciales sean tales que la enfermedad se autocontrola.

ID:(4075, 0)


Factor de reproducción, modelo SIR
Ecuación

>Top, >Modelo


Al ser critico el factor que compara los factores propios del contagio \beta C con el propio de recuperación \gamma que se le denomina factor de reproducción y designa por la letra

$R_0=\displaystyle\frac{\beta C}{\gamma}$

Como referencia se listan factores de reproducción de las enfermedades más típicas:

DiseaseTransmission$R_0$
Measlesdroplets in suspension12-18
Whooping coughdroplets in suspension12-17
Diphtheriasaliva6-7
Smallpoxdroplets in suspension5-7
Poliofecal-oral route5-7
Rubelladroplets in suspension5-7
Mumpsdroplets in suspension4-7
HIV / AIDSsexual contact2-5
SARSdroplets in suspension2-5
Influenza (1918 pandemic strain)droplets in suspension2-3
Ebolabody fluids1.5-2.5

ID:(4074, 0)


Limite de contención
Ecuación

>Top, >Modelo


Otra de las aplicaciones de la ecuación es la de permitir estimar las medidas necesarias para evitar la epidemia. En general se necesita que la población susceptible sea menor que el valor crítico.

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{\gamma}{C\beta}$

\\n\\nLa reducción de S se logra con una vacunación preventiva. Si se supone que el publico en general no modifica sus costumbres para reducir \beta y C, y no tenemos medicinas para aumentar el factor \gamma podemos 'pasar' personas del estado S al R vía vacunación. Si q es la fracción a vacunar debe ser tal que\\n\\n

$S_{crit}=(1-q)S$



Con el factor de recuperación

$R_0=\displaystyle\frac{\beta C}{\gamma}$

\\n\\nse tiene que\\n\\n

$q=1-\displaystyle\frac{1}{R_0}\displaystyle\frac{N}{S}$



Si se supone que inicialmente los susceptibles son iguales a la población (S\sim N) se tiene que el universo a vacunar es igual a

$q=1-\displaystyle\frac{1}{R_0}$

lo que nos da una idea del nivel de masividad que debe tener la campaña de vacunación.

Como ejemplo en las enfermedades consideradas se tiene que:

|Enfermedad|Transmisión|Vacunación|

|:---------|:----------|:---------:|

|Sarampión|gotitas en suspensión|92-94%|

|Tos ferina|gotitas en suspensión|92-94%|

|Difteria|saliva|83-86%|

|Viruela|gotitas en suspensión|80-86%|

|Polio|ruta fecal-oral|80-86%|

|Rubéola|gotitas en suspensión|80-86%|

|Paperas|gotitas en suspensión|75-86%|

|VIH/SIDA|contacto sexual|50-80%|

|SARS|gotitas en suspensión|50-80%|

|Influenza (1918 cepa pandémica)|gotitas en suspensión|50-67%|

|Ébola|fluidos corporales|34-60%|

ID:(4076, 0)


Simulación del modelo SIR
Html

>Top


El modelo se puede resolver numéricamente las ecuaciones para los susceptibles S, infectados I y recuperados R:

$\displaystyle\frac{dS}{dt}=-C\displaystyle\frac{I}{N}S\beta$



$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I$



$\displaystyle\frac{dR}{dt}=\gamma I$

en donde t es el tiempo \beta la taza de contagio, \gamma la taza de recuperación, C el número de contactos y N la población.

ID:(3022, 0)


Modelo SIR para describir SARS 2003 en Hong Kong
Imagen

>Top


Si se observan los susceptibles, infectados y 'recuperados' (que se sanan o mueren) se observan las típicas curvas del modelo SIR:

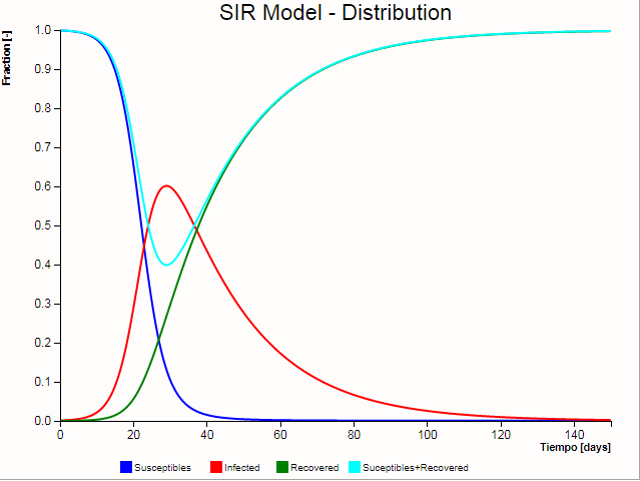
ID:(9663, 0)