Usuario:


Modelo SEIR
Storyboard

>Modelo

ID:(349, 0)


Modelos SEIR modificados
Descripción

>Top


Modelos que incluyen los casos en que existen personas infectadas pero que aun no muestran síntomas y no contagian. Dichas personas se denominan personas latentes.

ID:(873, 0)


Ecuación de susceptibles en el modelo SEIR
Ecuación

>Top, >Modelo


En el caso de los susceptibles el proceso de generar personas latentes en el modelo SEIR es equivalente a la de crear infectados en el modelo SIR. Por ello en este caso la ecuación que describe los susceptibles es igual en ambos modelos:

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$

ID:(4086, 0)


Ecuación de latentes del modelo SEIR
Ecuación

>Top, >Modelo


En el caso de la ecuación de los casos latentes se tiene que primero considerar aquellos que se han contagiado y que el el modelo SIR conducía a los infectados\\n\\n

$-\displaystyle\frac{\beta C}{N}I(t)S(t)$

\\n\\ndonde \beta es la probabilidad de infectados, C el número de contactos, S el numero de los susceptibles, I el numero de los infectados y N el numero de la población.\\n\\nEl numero de latentes descenderá en función de la fracción \sigma que pase a mostrar los síntomas y ser parte de los infectados con síntomas I\\n\\n

$-\sigma E(t)$

\\n\\nDe igual forma se deben considerar aquellos que mueren por otra causa\\n\\n

$-\mu_d E(t)$



por lo que la ecuación para describir a los latentes será

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$

ID:(4087, 0)


Ecuación de infectados en el modelo SEIR
Ecuación

>Top, >Modelo


En el caso de la ecuación de los casos infectado se tiene que primero considerar aquellos que son latentes E y que en la proporción \sigma pasan a estar infectados

\sigma E(t)

El numero de infectados descenderá en función de la fracción \gamma de los infectados I que se recupera

-\gamma I(t)

De igual forma se deben considerar aquellos que mueren por otra causa

-\mu_d I(t)

por lo que la ecuación para describir a los infectados será

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$

ID:(4088, 0)


Ecuación de recuperados en el modelo SEIR
Ecuación

>Top, >Modelo


En el caso de la ecuación de los casos recuperados, se tiene que primero considerar aquellos que son infectados I y que en la proporción \gamma pasan a estar recuperados\\n\\n

$\gamma I(t)$

\\n\\nDe igual forma se deben considerar aquellos que mueren por otra causa\\n\\n

$-\mu_d R(t)$



por lo que la ecuación para describir a los infectados será

$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

ID:(4089, 0)


Factor de reproducción en el modelo de SEIR
Ecuación

>Top, >Modelo


Si la probabilidad de infectarse es \beta, el número de contactos C, el factor de reproducción \gamma, el factor de paso de latente a infectado y \mu_d el factor de muerte por otras causas, el factor de reproducción es

$R_0=\displaystyle\frac{\beta C\sigma}{(\sigma+\mu_d)(\gamma+\mu_d)}$

ID:(4093, 0)


Número de susceptibles críticos, modelo SEIR
Ecuación

>Top, >Modelo


En el caso crítico en que el sistema se vuelve estable el numero de latentes E no variara

$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$



y los infectados I

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$



en donde S es el numero de susceptibles, \beta es la probabilidad de infectar, C numero de contactos, N numero de población, \gamma es el factor de recuperación, \mu_b el factor de nacimiento y \mu_d el de muerte.

El numero de latentes críticos se puede despejar de la segunda ecuación

$\displaystyle\frac{E_{crit}}{N}=\displaystyle\frac{(\gamma+\mu_d)}{\sigma}\displaystyle\frac{I_{crit}}{N}$



Si se reemplaza este valor en la primera ecuación se obtiene el valor críticos para los susceptibles

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{(\sigma+\mu_d)(\gamma+\mu_d)}{\beta C\sigma}$

que corresponde a la situación en que la curva de infectados alcanza su máximo. Es decir el número de susceptibles críticos es el numero de susceptibles que van quedando al momento que el número de infectados alcanza su máximo.

ID:(4090, 0)


Número de latentes críticos, modelo SEIR
Ecuación

>Top, >Modelo


De la ecuación de los infectados I

$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$



en que \gamma es el factor de recuperación, \sigma el factor de paso de latente a infectado, E los latentes y \mu_d el factor de los muertos.

Como el número de susceptibles en el caso críticos es

$\displaystyle\frac{I_{crit}}{N}=\displaystyle\frac{\mu_bN-\mu_dS_{crit}}{{\beta C S_{crit}}}$



se puede calcular el número crítico de los infectados

$\displaystyle\frac{E_{crit}}{N}=\displaystyle\frac{(\gamma+\mu_d)}{\sigma}\displaystyle\frac{I_{crit}}{N}$

que corresponde a la situación en que la curva de infectados alcanza su máximo. Es decir el número de latentes críticos es el numero de latentes que van quedando al momento que el número de infectados alcanza su máximo.

ID:(4092, 0)


Número de infectados críticos, modelo SEIR
Ecuación

>Top, >Modelo


De la ecuación de los susceptibles S

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$



en que \beta es la probabilidad de infección, C el número de contactos, N el número de la población, I los infectados, \mu_b el factor de los nacimientos y \mu_d el factor de los muertos.

Como el número de susceptibles en el caso asintótico es

$\displaystyle\frac{S_{crit}}{N}=\displaystyle\frac{(\sigma+\mu_d)(\gamma+\mu_d)}{\beta C\sigma}$



se puede calcular el número asintotico de los infectados

$\displaystyle\frac{I_{crit}}{N}=\displaystyle\frac{\mu_bN-\mu_dS_{crit}}{{\beta C S_{crit}}}$

ID:(4091, 0)


Curva del modelo SEIR
Imagen

>Top


En el caso de los modelos SEIR se tienen cuatro curvas, la de susceptibles, latentes, infectados y recuperados:

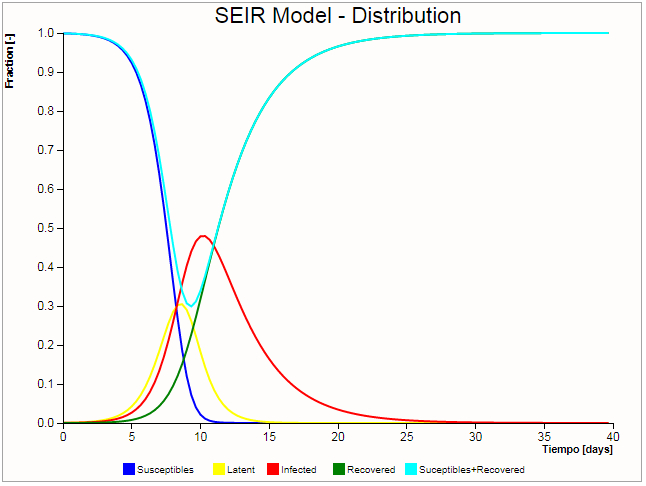
ID:(9703, 0)


Simulación del modelo SEIR
Html

>Top


El modelo se puede resolver numéricamente las ecuaciones para los susceptibles S, infectados I, latentes E y recuperados R:

$\displaystyle\frac{dS}{dt}=-\displaystyle\frac{\beta C}{N}I(t)S(t)+\mu_bN-\mu_dS(t)$



$\displaystyle\frac{dE}{dt}=\displaystyle\frac{\beta C}{N}I(t)S(t)-(\sigma+\mu_d)E(t)$



$\displaystyle\frac{dI}{dt}=\sigma E(t)-(\gamma+\mu_d)I(t)$



$\displaystyle\frac{dR}{dt}=\gamma I(t)-\mu_dR(t)$

en donde t es el tiempo \beta la taza de contagio, \sigma la taza de surgimiento de los síntomas en los infectados, \gamma la taza de recuperación, C el número de contactos, N la población, \mu_b la natalidad por habitante y \mu_d la mortalidad por habitante.

ID:(6834, 0)