Utilizador:
Força da gravidade e marés em conjunto
Storyboard 
A gravidade e a aceleração centrífuga geram as marés, o movimento dos oceanos que eleva e reduz seu nível com uma frequência de 12 horas. Sua origem pode ser tanto gerada pela lua quanto pelo sol.
ID:(1523, 0)
Variação da gravidade perpendicular ao raio, em conjunto
Imagem
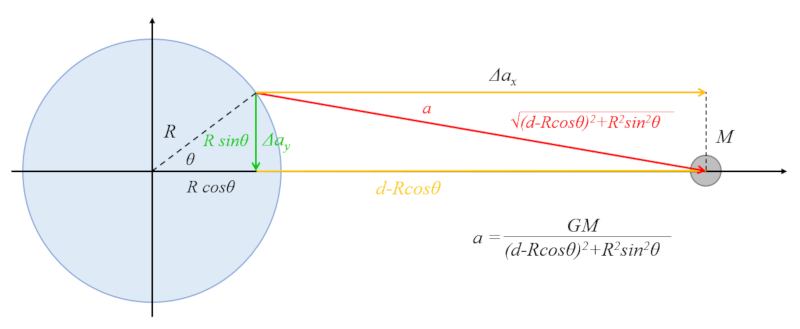
Existe uma contribuição da atração gravitacional do corpo celeste que atrai a água em direção à região equatorial:
A hipotenusa do triângulo está relacionada com o cateto vertical pela expressão:
$R\sin\theta$
e com o cateto horizontal por:
$d - R\cos\theta$
De acordo com o teorema de Pitágoras, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa, então temos:
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11635, 0)
Variação da gravidade paralela ao raio, em conjunto
Imagem
Existe uma contribuição da atração gravitacional do corpo celeste que atrai a água em direção ao raio, o que tende a deslocar a água em direção à zona do equador:
A hipotenusa do triângulo é formada pelo cateto vertical:
$R\sin\theta$
e pelo cateto horizontal:
$d - R\cos\theta$
De acordo com o teorema de Pitágoras, temos:
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11658, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$
a_c = G * M /( d ^2+ R ^2-2* d * R *cos( theta ))
$ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cx / a_c = ( d - R * cos( theta ))/sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_cx = G * M *(1 + 2* R * cos( theta )/ d )/ d ^2
$ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cy / a_c = R * sin( theta ) / sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$
Da_cy = G * M * R * sin( theta )/ d ^3
ID:(15434, 0)
Variação da aceleração perpendicular ao raio, em conjunto
Equação
Para determinar a variação da aceleração perpendicular ao raio, podemos utilizar a semelhança de triângulos para igualar a relação
$\displaystyle\frac{\Delta a_{cy}}{a_c}$
com o comprimento
$d-R\cos\theta$
e a hipotenusa
$\sqrt{d^2+R^2-2dR\cos\theta}$
.
Pela semelhança de triângulos, temos com que
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
.
ID:(11643, 0)
Aceleração perpendicular ao raio, em conjunto
Equação
Com a lei da gravitação de Newton, com , temos:
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
É possível, com a definição da força, com :
| $ F = m_i a $ |
E o raio ao quadrado:
$r^2=d^2+R^2-2dR\cos\theta$
Calcular a aceleração substituindo o raio na força e resolvendo a equação da aceleração. Isso resulta em a aceleração:
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
ID:(11644, 0)
Aceleração de aproximação perpendicular ao raio, em conjunto
Equação
Com , a relação entre a variação da aceleração e a aceleração é:
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
E como a expressão para a aceleração é com :
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
Segue que:
$\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}$
Portanto, na aproximação
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
ID:(11645, 0)
Variação da aceleração paralela ao raio, em conjunto
Equação
Para determinar a variação da aceleração paralela ao raio, podemos utilizar a semelhança de triângulos para igualar a relação
$\displaystyle\frac{\Delta a_{cx}}{a_c}$
com o comprimento
$d+R\cos\theta$
e a hipotenusa
$\sqrt{d^2+R^2-2dR\cos\theta}$
Por semelhança de triângulos, temos com que
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
ID:(11647, 0)
Aceleração de aproximação paralela ao raio, em conjunto
Equação
Com e raio do planeta $m$, a relação é:
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
E como para e raio do planeta $m$,
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
Assim, temos:
$\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)$
Portanto, na aproximação
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11650, 0)