Usuario:
Fuerza de gravedad y mareas en conjunción
Storyboard 
La gravedad y la aceleración centrífuga son responsables de las mareas, el movimiento de los océanos que eleva y reduce su nivel con una frecuencia de 12 horas. Su origen puede ser tanto la Luna como el Sol.
ID:(1523, 0)
Variación de la gravedad perpendicular al radio, en conjunción
Imagen
La atracción gravitatoria de un cuerpo celeste provoca el fenómeno de la marea, desplazando el agua hacia la región ecuatorial. Esto se ilustra en el siguiente diagrama:
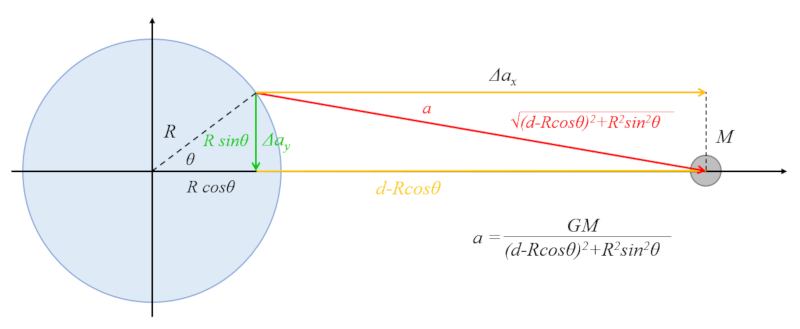
En el triángulo mostrado, la hipotenusa se relaciona con el cateto vertical por la expresión:
$R\sin\theta$
y con el cateto horizontal por:
$d - R\cos\theta$
De acuerdo con el teorema de Pitágoras, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, por lo que obtenemos:
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11635, 0)
Variación de la gravedad paralelo al radio, en conjunción
Imagen
Existe uma contribuição da atração do corpo celeste que direciona a água em direção ao raio, o que tende a deslocar a água em direção à zona do equador:
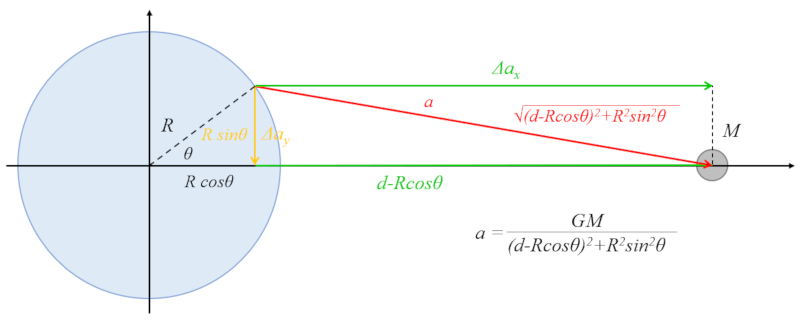
A hipotenusa do triângulo é dada pelo cateto vertical:
$R\sin\theta$
e pelo cateto horizontal:
$d - R\cos\theta$
De acordo com o teorema de Pitágoras, temos:
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11658, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$
a_c = G * M /( d ^2+ R ^2-2* d * R *cos( theta ))
$ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cx / a_c = ( d - R * cos( theta ))/sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_cx = G * M *(1 + 2* R * cos( theta )/ d )/ d ^2
$ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cy / a_c = R * sin( theta ) / sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$
Da_cy = G * M * R * sin( theta )/ d ^3
ID:(15434, 0)
Variación de aceleración perpendicular al radio, en conjunción
Ecuación
Para determinar la variación de la aceleración perpendicular al radio, podemos utilizar la similitud de triángulos para igualar la relación
$\displaystyle\frac{\Delta a_{cy}}{a_c}$
con el comprimento
$d-R\cos\theta$
y la hipotenusa
$\sqrt{d^2+R^2-2dR\cos\theta}$
.
Por la similitud de triángulos, tenemos con que
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
.
ID:(11643, 0)
Aceleración perpendicular al radio, en conjunción
Ecuación
Con la ley de la gravitación de Newton con es:
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
Se puede, con la definición de la fuerza con :
| $ F = m_i a $ |
Y el radio al cuadrado:
$r^2=d^2+R^2-2dR\cos\theta$
Calcular la aceleración reemplazando el radio en la fuerza y despejando la aceleración. Lo que da con la aceleración:
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
ID:(11644, 0)
Aproximación aceleración perpendicular al radio, en conjunción
Ecuación
Con , la relación entre la variación de la aceleración y la aceleración es:
Y dado que la expresión para la aceleración es con :
Se sigue que:
$\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}$
Por lo tanto, en la aproximación
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
ID:(11645, 0)
Variación de aceleración paralelo al radio, en conjunción
Ecuación
Para determinar a variação da aceleração paralela ao raio, podemos utilizar a semelhança de triângulos para igualar a relação
$\displaystyle\frac{\Delta a_{cx}}{a_c}$
com o comprimento
$d+R\cos\theta$
e a hipotenusa
$\sqrt{d^2+R^2-2dR\cos\theta}$
Por semelhança de triângulos, temos com que
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
ID:(11647, 0)
Aproximación aceleración paralelo al radio, en conjunción
Ecuación
Con aceleración generada por el cuerpo celeste, en conjunción $m/s^2$, ángulo desde la línea planeta - objeto celeste $rad$, distancia planeta objeto celeste $m$, radio del planeta $m$ y variación de aceleración paralelo a la eclíptica, en conjución $m/s^2$, la relación es:
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
Y como para aceleración generada por el cuerpo celeste, en conjunción $m/s^2$, ángulo desde la línea planeta - objeto celeste $rad$, constante Universal de Gravitación $m^3/kg s^2$, distancia planeta objeto celeste $m$, masa del cuerpo que genera la marea $kg$ y radio del planeta $m$,
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
Entonces, se sigue que:
$\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)$
Por lo tanto, en la aproximación
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11650, 0)