Utilizador:
Força da gravidade e marés em oposição
Storyboard 
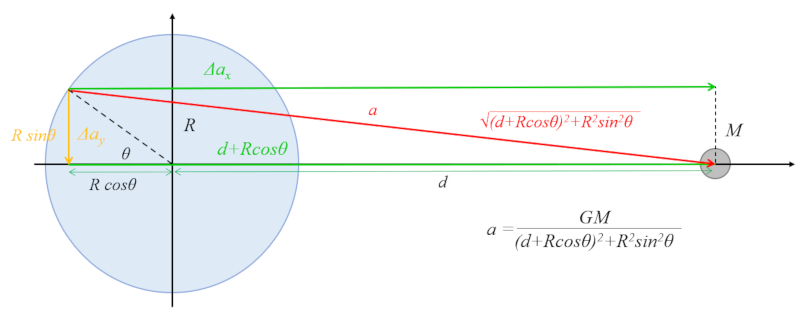
Uma das acelerações que precisa ser calculada é aquela paralela à eclíptica (no plano Terra-corpo celeste) em oposição, ou seja, do lado oposto ao lado onde está o corpo celeste.
ID:(1575, 0)
Variação da gravidade paralela ao raio, em oposição
Imagem
A atração no lado oposto ao corpo celeste que atua sobre a Terra é menor devido ao efeito da maior distância. Isso facilita o deslocamento da água em direção ao equador. Por outro lado, do lado voltado para o corpo celeste, sua atração enfraquece a aceleração gravitacional da Terra, levando a uma redução da gravidade que favorece ainda mais o deslocamento da água em direção ao equador:
Neste caso, trabalhamos com a semelhança no triângulo, onde tomamos a proporção
$\Delta a_{ox}/a_o$
e o cateto
$d + R\cos\theta$
e a hipotenusa
$(d+R\cos\theta)^2+R^2\sin^2\theta=d^2+R^2+2dR\cos\theta$
ID:(11639, 0)
Explicação intuitiva da maré no lado oposto do corpo celeste
Imagem
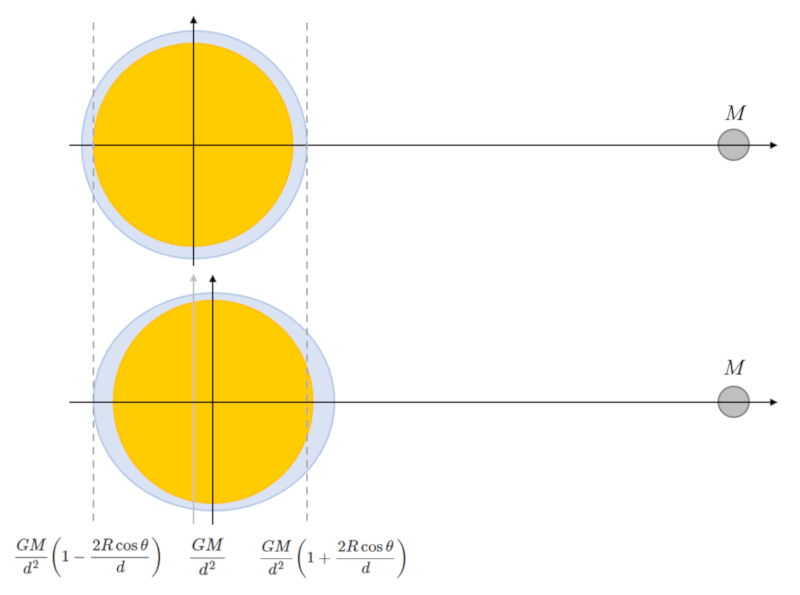
Existem múltiplas explicações para as marés no lado oposto do corpo celeste. Uma delas é o efeito da aceleração centrífuga devido ao fato de o sistema girar em torno do centro de massa do sistema Terra-corpo celeste, que não está no centro da Terra. No entanto, os valores obtidos para o caso da Lua são muito diferentes no lado voltado para a Lua em comparação com o lado oposto da Terra. Além disso, seria complicado explicar o fenômeno dessa forma se considerarmos o Sol como o corpo celeste, já que nesse caso o centro de massa está próximo ao centro do Sol.
A forma mais simples e que produz valores observados é supor que é um problema de diferenças de gravidade e deslocamento dos objetos. Portanto:
• A maré em direção ao lado do corpo celeste é originada pela sua atração, que reduz a aceleração gravitacional da Terra.
• A maré no lado oposto do corpo celeste ocorre tanto devido à redução da atração do corpo celeste quanto ao fato de que a Terra é deslocada "dentro da água".
ID:(11640, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$
a_o = G * M /( d ^2 + R ^2 + 2* d * R * cos( theta ))
$ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$
Da_ox / a_o = ( d + R * cos( theta ))/sqrt( d ^2 + R ^2 + 2 * d * R * cos( theta ))
$ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_ox = G * M * (1-2* R * cos( theta )/ d )/ d ^2
ID:(15435, 0)
Variação da aceleração paralela ao raio, em oposição
Equação
Para determinar a variação da aceleração no raio, podemos igualar a relação
$\displaystyle\frac{\Delta a_{ox}}{a_o}$
com o comprimento
$d+R\cos\theta$
e a hipotenusa
$\sqrt{d^2+R^2+2dR\cos\theta}$
Por semelhança de triângulos, obtemos com que:
| $ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$ |
ID:(11646, 0)
Aceleração paralela ao raio, em oposição
Equação
Com a lei da gravitação de Newton, representada por ,
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
,
podemos definir a força com ,
| $ F = m_i a $ |
,
e o raio ao quadrado
$r^2=d^2+R^2+2dR\cos\theta$
,
para calcular a aceleração com :
| $ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$ |
ID:(11651, 0)
Aceleração de aproximação paralela ao raio, em oposição
Equação
Com e raio do planeta $m$, a relação é
| $ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$ |
,
e com e raio do planeta $m$, a expressão é
| $ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$ |
,
assim
$\Delta a_{ox} =GM\displaystyle\frac{d + R\cos\theta}{(d^2 + R^2 + 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1-\displaystyle\frac{2R\cos\theta}{d}\right)$
,
então na aproximação $d\gg R$ e considerando apenas a variação em relação ao lado oposto, pode ser aproximado com e raio do planeta $m$ como:
| $ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11649, 0)