Benützer:


Entropie
Storyboard

Entropie ist der Teil der Energie in einem System, der nicht genutzt werden kann, um Arbeit zu verrichten. Aus mikroskopischer Sicht bezieht sie sich auf die Anzahl möglicher Konfigurationen, die das System annehmen kann. Eine größere Anzahl dieser Konfigurationen steht in Verbindung mit einer Zunahme der Unordnung im System und einer Abnahme der Wahrscheinlichkeit, dass das System in einen früheren Zustand zurückkehrt, wodurch die Möglichkeit der Reversibilität des Systems verringert wird.

>Modell

ID:(1471, 0)


Mechanismen
Definition

Die physikalische Entropie ist ein grundlegendes Konzept in der Thermodynamik und der statistischen Mechanik, das den Grad der Unordnung oder Zufälligkeit in einem System darstellt. Sie misst die Anzahl der spezifischen Anordnungen, in denen ein thermodynamisches System existieren kann, und spiegelt die Menge an Ungewissheit oder die Anzahl möglicher Mikrozustände wider, die einem gegebenen Makrozustand entsprechen. Entropie quantifiziert Unordnung, wobei eine höhere Entropie auf eine größere Unordnung hinweist. Laut dem zweiten Gesetz der Thermodynamik nimmt die Entropie eines isolierten Systems niemals ab, was bedeutet, dass natürliche Prozesse dazu tendieren, sich zu einem Zustand maximaler Entropie oder Unordnung zu bewegen. Die Entropie misst auch die Irreversibilität von Prozessen, wobei spontane Prozesse die Entropie des Universums erhöhen. Sie ist ein Schlüsselfaktor für die Bestimmung der Effizienz von Wärmekraftmaschinen und Kühlschränken, das Verständnis des Verhaltens biologischer Systeme und das Studium der Entwicklung des Universums. Im Wesentlichen ist die Entropie ein Maß für die Unvorhersehbarkeit und Energiedispersion in einem System und gibt Aufschluss über die natürliche Tendenz zur Unordnung und die Begrenzungen der Energieumwandlung.

ID:(15246, 0)


Arten von Variablen
Bild

Wenn wir die Gleichung von ERROR:5221,0 mit die Mechanische Kraft ($F$) und der Zurückgelegter Weg ($dx$) betrachten:

$ \Delta W = F \Delta s $



in ihrer Form von die Druck ($p$) und der Volumen ($V$):

$ \delta W = p dV $



Spielt die Arbeit die Rolle eines Potenzials, während die Druck ($p$) als 'verallgemeinerte Kraft' fungiert und der Volumen ($V$) als der Pfad dient, eine Art 'unabhängige Variable'. Wenn wir diese Konzepte für die bisher besprochenen Parameter in einer Matrix organisieren, erhalten wir:

Thermodynamisches Potential Generalisierte Kraft Unabhängige Variable
Extensiv Intensiv Extensiv
$\delta W$ $p$ $dV$
$\delta Q$ $T$ $?$



In diesem Zusammenhang sehen wir, dass für die Zeile die Variation des Wärme ($\delta Q$) die Variable die Absolute Temperatur ($T$) vorhanden ist, aber uns eine extensiv unabhängige Variable fehlt. Diese nennen wir Entropie und bezeichnen sie mit dem Buchstaben $S$.

ID:(11183, 0)


Intensive und umfangreiche Variablen
Notiz

Es gibt Variablen, die mit Größen und andere, die mit Eigenschaften in Verbindung stehen.

• Die ersten werden als extensive Variablen bezeichnet, da sie proportional zur Menge der vorhandenen Substanz erweitert oder erhöht werden können. Beispiele für extensive Variablen sind Volumen, Masse, elektrische Ladung, Wärme usw.

• Die zweiten werden als intensive Variablen bezeichnet und repräsentieren Eigenschaften, die unabhängig von der Menge der Substanz sind. Diese Eigenschaften ändern sich nicht, wenn sich die Menge der Substanz ändert. Beispiele für intensive Variablen sind Dichte, Druck, Temperatur usw.

ID:(11182, 0)


Entropie und Phasenwechsel
Zitat

Wenn die Entropie in Abhängigkeit von der Temperatur geschätzt wird, kann Folgendes beobachtet werden:

• In jeder Phase (fest, flüssig, gasförmig) tendiert die Entropie dazu, mit steigender Temperatur leicht zu wachsen.
• Bei jedem Phasenübergang gibt es einen Sprung in der Entropie.

Dies kann wie folgt dargestellt werden:

Auf diese Weise kann die Entropie als ein Maß für die Freiheitsgrade eines Systems verstanden werden. Während sie in einer Phase allmählich zunimmt, weil nur wenige neue Freiheitsgrade freigesetzt werden, erfolgt bei Phasenübergängen ein deutlicher Anstieg. Ein Festkörper besteht aus vielen Bindungen, die die Bewegung der Atome einschränken. In einer Flüssigkeit gehen viele Bindungen verloren, wodurch neue Freiheiten entstehen, die relative Bewegungen ermöglichen und mit vielen neuen Freiheitsgraden verbunden sind. Schließlich gehen bei Übergang in den gasförmigen Zustand alle Bindungen verloren, und jedes Teilchen hat drei Freiheitsgrade. Bei weiter steigender Temperatur können die Teilchen rotieren und schwingen, was neue Freiheitsgrade und weitere Anstiege in der Entropie bedeutet.

ID:(11187, 0)


Entropie und Irreversibilität
Übung

Wenn wir zwei identische Systeme betrachten, eines mit einer Temperatur $T_1$ und das andere mit einer Temperatur $T_2$, können ihre Entropien mithilfe der Gleichung berechnet werden, in der die Entropie ($S$), die Absolute Temperatur ($T$), die Kalorische Kapazität ($C$), die Basisentropie ($S_0$) und die Basistemperatur ($T_0$) vorkommen:

$ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$



Daher lauten die Entropien:

$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$



und

$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$



Wenn beide Systeme gemischt werden, ergibt sich ihre Temperatur als Durchschnittstemperatur:

$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$



Daher wird die Entropie des neuen Systems sein:

$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$



Die Entropie des neuen Systems ist größer als die Summe der individuellen Entropien:

$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$



Wenn wir $\Delta S/C$ als Funktion von $T_1/T_0$ und $T_2/T_0$ grafisch darstellen, erhalten wir folgende Abbildung:

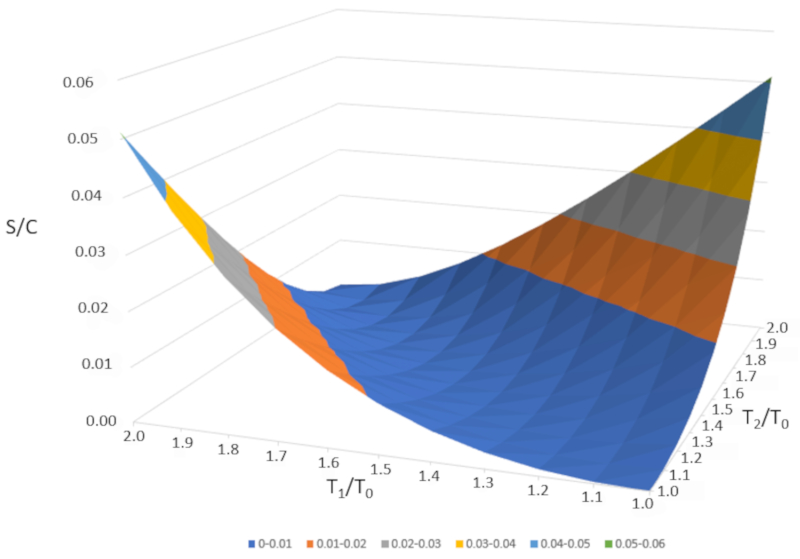
$\Delta S/C$ ist nahezu null, wenn die Temperaturen sehr ähnlich sind ($T_1\sim T_2$). Wenn die Temperaturen jedoch unterschiedlich sind, wird die Entropie immer zunehmen. Wenn wir dies in anderen Systemen untersuchen, werden wir feststellen, dass immer dann, wenn eine irreversible Änderung auftritt, die Entropie zunimmt. Das Mischen ist irreversibel, was bedeutet, dass das System nicht ohne äußere Eingriffe in seinen Ausgangszustand zurückkehrt. Mit anderen Worten, das System wird sich nicht spontan in zwei Teilsysteme mit völlig unterschiedlichen Temperaturen aufteilen.

ID:(11186, 0)


Modell
Gleichung


ID:(15305, 0)


Entropie
Beschreibung

Die physikalische Entropie ist ein grundlegendes Konzept in der Thermodynamik und der statistischen Mechanik, das den Grad der Unordnung oder Zufälligkeit in einem System darstellt. Sie misst die Anzahl der spezifischen Anordnungen, in denen ein thermodynamisches System existieren kann, und spiegelt die Menge an Ungewissheit oder die Anzahl möglicher Mikrozustände wider, die einem gegebenen Makrozustand entsprechen. Entropie quantifiziert Unordnung, wobei eine höhere Entropie auf eine größere Unordnung hinweist. Laut dem zweiten Gesetz der Thermodynamik nimmt die Entropie eines isolierten Systems niemals ab, was bedeutet, dass natürliche Prozesse dazu tendieren, sich zu einem Zustand maximaler Entropie oder Unordnung zu bewegen. Die Entropie misst auch die Irreversibilität von Prozessen, wobei spontane Prozesse die Entropie des Universums erhöhen. Sie ist ein Schlüsselfaktor für die Bestimmung der Effizienz von Wärmekraftmaschinen und Kühlschränken, das Verständnis des Verhaltens biologischer Systeme und das Studium der Entwicklung des Universums. Im Wesentlichen ist die Entropie ein Maß für die Unvorhersehbarkeit und Energiedispersion in einem System und gibt Aufschluss über die natürliche Tendenz zur Unordnung und die Begrenzungen der Energieumwandlung.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$s_L$
s_L
Molare Entropie der Flüssigkeit
J/K mol
$s_{L,m}$
s_Lm
Molare Entropie der Flüssigkeit beim Schmelzen
J/K mol
$s_{L,b}$
s_Lb
Molare Entropie der Flüssigkeit beim Sieden
J/K mol
$s_{S,m}$
s_Sm
Molare Entropie des Festkörpers beim Schmelzen
J/K mol
$s_S$
s_S
Molare Entropie des Feststoffs
J/K mol
$s_G$
s_G
Molare Entropie des Gases (oder Dampfes)
J/K mol
$s_{G,b}$
s_Gb
Molare Entropie des Gases beim Sieden
J/K mol
$l_S$
l_S
Molare latente Gefrierwärme
J/kg
$l_V$
l_V
Molare latente Verdampfungswärme
J/kg
$c_L$
c_L
Molare Wärmekapazität der Flüssigkeit
J/mol K
$c_S$
c_S
Molare Wärmekapazität des Festkörpers
J/mol K
$c_G$
c_G
Molare Wärmekapazität eines Gases
J/mol K
$T_{sl}$
T_sl
Schmelztemperatur
K
$T_{lg}$
T_lg
Siedetemperatur
K
$T_L$
T_L
Temperatur der Flüssigkeit
K
$T_S$
T_S
Temperatur des Festkörpers
K
$T_G$
T_G
Temperatur des Gases (Dampf)
K

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Um das Konzept der Entropie besser zu verstehen, kann man sich ein System im festen Zustand vorstellen, in dem die Atome geordnet angeordnet sind und die Entropie niedrig ist.

Wenn dem System Energie zugef hrt wird, beginnen die Atome mit gr erer Amplitude zu schwingen, und die Ordnung nimmt allm hlich ab. Beim Erreichen der Schmelztemperatur werden einige Teilchen aus ihren festen Positionen gel st und erhalten mehr Bewegungsfreiheit innerhalb der Materialmatrix. Dieser erh hte Grad an Unordnung f hrt zu einem Anstieg der Entropie.

Wird weiter Energie zugef hrt und die Siedetemperatur erreicht, beginnen die Teilchen das System zu verlassen und gehen in den gasf rmigen Zustand ber. Dies ist der Zustand mit der gr ten Bewegungsfreiheit und Unordnung also mit der h chsten Entropie. Wenn das System schlie lich vollst ndig verdampft ist, wird ein Maximum an Entropie erreicht.

(ID 15246)

Wenn wir die Gleichung von ERROR:5221,0 mit die Mechanische Kraft ($F$) und der Zurückgelegter Weg ($dx$) betrachten:

$ \Delta W = F \Delta s $



in ihrer Form von die Druck ($p$) und der Volumen ($V$):

$ \delta W = p dV $



Spielt die Arbeit die Rolle eines Potenzials, w hrend die Druck ($p$) als 'verallgemeinerte Kraft' fungiert und der Volumen ($V$) als der Pfad dient, eine Art 'unabh ngige Variable'. Wenn wir diese Konzepte f r die bisher besprochenen Parameter in einer Matrix organisieren, erhalten wir:

Thermodynamisches Potential Generalisierte Kraft Unabh ngige Variable
Extensiv Intensiv Extensiv
$\delta W$ $p$ $dV$
$\delta Q$ $T$ $?$



In diesem Zusammenhang sehen wir, dass f r die Zeile die Variation des Wärme ($\delta Q$) die Variable die Absolute Temperatur ($T$) vorhanden ist, aber uns eine extensiv unabh ngige Variable fehlt. Diese nennen wir Entropie und bezeichnen sie mit dem Buchstaben $S$.

(ID 11183)

Es gibt Variablen, die mit Gr en und andere, die mit Eigenschaften in Verbindung stehen.

• Die ersten werden als extensive Variablen bezeichnet, da sie proportional zur Menge der vorhandenen Substanz erweitert oder erh ht werden k nnen. Beispiele f r extensive Variablen sind Volumen, Masse, elektrische Ladung, W rme usw.

• Die zweiten werden als intensive Variablen bezeichnet und repr sentieren Eigenschaften, die unabh ngig von der Menge der Substanz sind. Diese Eigenschaften ndern sich nicht, wenn sich die Menge der Substanz ndert. Beispiele f r intensive Variablen sind Dichte, Druck, Temperatur usw.

(ID 11182)

Wenn die Entropie in Abh ngigkeit von der Temperatur gesch tzt wird, kann Folgendes beobachtet werden:

• In jeder Phase (fest, fl ssig, gasf rmig) tendiert die Entropie dazu, mit steigender Temperatur leicht zu wachsen.
• Bei jedem Phasen bergang gibt es einen Sprung in der Entropie.

Dies kann wie folgt dargestellt werden:

Auf diese Weise kann die Entropie als ein Ma f r die Freiheitsgrade eines Systems verstanden werden. W hrend sie in einer Phase allm hlich zunimmt, weil nur wenige neue Freiheitsgrade freigesetzt werden, erfolgt bei Phasen berg ngen ein deutlicher Anstieg. Ein Festk rper besteht aus vielen Bindungen, die die Bewegung der Atome einschr nken. In einer Fl ssigkeit gehen viele Bindungen verloren, wodurch neue Freiheiten entstehen, die relative Bewegungen erm glichen und mit vielen neuen Freiheitsgraden verbunden sind. Schlie lich gehen bei bergang in den gasf rmigen Zustand alle Bindungen verloren, und jedes Teilchen hat drei Freiheitsgrade. Bei weiter steigender Temperatur k nnen die Teilchen rotieren und schwingen, was neue Freiheitsgrade und weitere Anstiege in der Entropie bedeutet.

(ID 11187)

Wenn wir zwei identische Systeme betrachten, eines mit einer Temperatur $T_1$ und das andere mit einer Temperatur $T_2$, k nnen ihre Entropien mithilfe der Gleichung berechnet werden, in der die Entropie ($S$), die Absolute Temperatur ($T$), die Kalorische Kapazität ($C$), die Basisentropie ($S_0$) und die Basistemperatur ($T_0$) vorkommen:

$ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$



Daher lauten die Entropien:

$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$



und

$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$



Wenn beide Systeme gemischt werden, ergibt sich ihre Temperatur als Durchschnittstemperatur:

$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$



Daher wird die Entropie des neuen Systems sein:

$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$



Die Entropie des neuen Systems ist gr er als die Summe der individuellen Entropien:

$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$



Wenn wir $\Delta S/C$ als Funktion von $T_1/T_0$ und $T_2/T_0$ grafisch darstellen, erhalten wir folgende Abbildung:

$\Delta S/C$ ist nahezu null, wenn die Temperaturen sehr hnlich sind ($T_1\sim T_2$). Wenn die Temperaturen jedoch unterschiedlich sind, wird die Entropie immer zunehmen. Wenn wir dies in anderen Systemen untersuchen, werden wir feststellen, dass immer dann, wenn eine irreversible nderung auftritt, die Entropie zunimmt. Das Mischen ist irreversibel, was bedeutet, dass das System nicht ohne u ere Eingriffe in seinen Ausgangszustand zur ckkehrt. Mit anderen Worten, das System wird sich nicht spontan in zwei Teilsysteme mit v llig unterschiedlichen Temperaturen aufteilen.

(ID 11186)


(ID 15305)

Wenn die Temperatura de fusión ($T_f$) die Siedetemperatur darstellt, die Molare Entropie der Flüssigkeit ($s_L$) der molaren Entropie der Fl ssigkeit entspricht und die Molare Entropie des Feststoffs ($s_S$) der des Feststoffs, dann wird die Verdampfungsenthalpie die Calor latente molar del cambio de fase solido liquido ($l_S$) mit der folgenden Formel berechnet:

$ l_{sl} = T_{sl} ( s_{lm} - s_{sm} )$

(ID 9051)

Wenn die Siedetemperatur ($T_b$) die Siedetemperatur ist, die Molare Entropie des Gases (oder Dampfes) ($s_G$) die molare Entropie des Dampfes darstellt und die Molare Entropie der Flüssigkeit ($s_L$) die des Fl ssigkeit, dann wird die Verdampfungsenthalpie die Calor latente molar del cambio de fase liquido vapor ($l_V$) mit der folgenden Formel berechnet:

$ l_{lg} = T_{lg} ( s_{gb} - s_{lb} )$

(ID 9050)

Der Wert von die Molare Entropie ($s$) wird als Funktion von die Referenzmolarentropie ($s_0$) bestimmt, abh ngig von der Molare Wärmekapazität ($c$), ERROR:5199 und die Basistemperatur ($T_0$), gem :

$ s = s_0 + c \log\left(\displaystyle\frac{ T }{ T_0 }\right)$

(ID 16216)

Der Wert von die Molare Entropie ($s$) wird als Funktion von die Referenzmolarentropie ($s_0$) bestimmt, abh ngig von der Molare Wärmekapazität ($c$), ERROR:5199 und die Basistemperatur ($T_0$), gem :

$ s = s_0 + c \log\left(\displaystyle\frac{ T }{ T_0 }\right)$

(ID 16216)

Der Wert von die Molare Entropie ($s$) wird als Funktion von die Referenzmolarentropie ($s_0$) bestimmt, abh ngig von der Molare Wärmekapazität ($c$), ERROR:5199 und die Basistemperatur ($T_0$), gem :

$ s = s_0 + c \log\left(\displaystyle\frac{ T }{ T_0 }\right)$

(ID 16216)

Der Wert von die Molare Entropie ($s$) wird als Funktion von die Referenzmolarentropie ($s_0$) bestimmt, abh ngig von der Molare Wärmekapazität ($c$), ERROR:5199 und die Basistemperatur ($T_0$), gem :

$ s = s_0 + c \log\left(\displaystyle\frac{ T }{ T_0 }\right)$

(ID 16216)

Der Wert von die Molare Entropie ($s$) wird als Funktion von die Referenzmolarentropie ($s_0$) bestimmt, abh ngig von der Molare Wärmekapazität ($c$), ERROR:5199 und die Basistemperatur ($T_0$), gem :

$ s = s_0 + c \log\left(\displaystyle\frac{ T }{ T_0 }\right)$

(ID 16216)

ID:(1471, 0)