Calorimetria
Storyboard 
A calorimetria é o processo de medição do calor associado a uma mudança em uma variável de estado. Essas variáveis de estado incluem tipicamente a temperatura, a pressão e o volume, embora outras possam ser incluídas dependendo do estado que está sendo descrito.Quando se mede a variação da temperatura em relação ao calor fornecido ou extraído, fala-se em capacidade térmica. No caso de um gás, a capacidade térmica é influenciada pelas demais variáveis de estado. Assim, a capacidade térmica é definida e medida a volume constante ou a pressão constante.
ID:(789, 0)
Mecanismos
Conceito 
A calorimetria é a ciência que mede a quantidade de calor envolvida em reações químicas, mudanças físicas ou capacidade calorífica. Ela quantifica o calor trocado nos processos, fornecendo dados essenciais sobre as mudanças de energia envolvidas. A calorimetria determina a capacidade calorífica das substâncias, indicando como diferentes materiais respondem ao calor. Também mede as mudanças de entalpia nas reações químicas, mostrando se são exotérmicas ou endotérmicas. Além disso, a calorimetria estuda as transições de fase, como fusão, ebulição ou sublimação, medindo o calor absorvido ou liberado. Os dados obtidos da calorimetria podem ser usados para derivar outras propriedades termodinâmicas, como entropia e energia livre de Gibbs, oferecendo uma compreensão completa do comportamento de um sistema. O princípio fundamental envolve o uso de um calorímetro para medir com precisão a troca de calor através do monitoramento das mudanças de temperatura, o que é crucial em campos como química, física, biologia e engenharia.
ID:(15244, 0)
Conversor trabalho-calor
Descrição 
A conversão de trabalho em energia é estudada através da geração de calor por meio do atrito. Para isso, envolve-se uma faixa metálica ao redor de um cilindro que contém água e um termômetro. Ao girar a manivela, o atrito gera calor, levando ao aquecimento da água. Se medirmos a força aplicada, o número de voltas realizadas e o raio do cilindro, é possível estimar a distância percorrida, o que nos permite estimar a energia como o produto da força pela distância.

ID:(1884, 0)
Conteúdo calórico de um sólido e líquido
Conceito 
Se uma amostra a uma determinada temperatura for imersa em um copo de água a uma temperatura mais baixa, observar-se-á um aumento da temperatura da água. Esse aumento dependerá da capacidade calorífica específica e da massa da amostra:
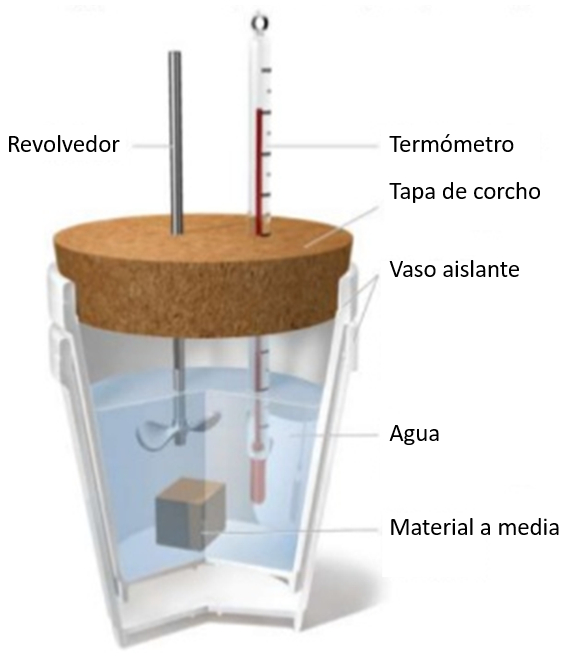
la calor fornecido ao líquido ou sólido ($\Delta Q$) está relacionado com la variação de temperatura ($\Delta T$) e la capacidade calórica ($C$) da seguinte forma:
| $ \Delta Q = C \Delta T $ |
Onde la capacidade calórica ($C$) pode ser substituído por o calor específico ($c$) e la massa ($M$) usando a seguinte relação:
| $ c =\displaystyle\frac{ C }{ M }$ |
Portanto, obtemos:
| $ \Delta Q = M c \Delta T$ |
ID:(15809, 0)
Aquecimento sob volume constante
Descrição 
Se um gás é aquecido, a capacidade calorífica depende da forma como isso ocorre. Uma forma é a volume constante, ou seja, o volume é mantido fixo enquanto o sistema é exposto a uma pressão maior ou menor:
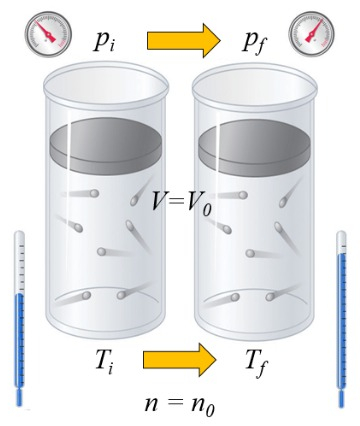
la capacidade calórica ($C$) em sólidos e líquidos pode ser considerado como uma constante $C$ que relaciona a variação de la calor fornecido ao líquido ou sólido ($\Delta Q$) e ERROR:7510 por meio da equação:
| $ \Delta Q = C \Delta T $ |
No caso em que o volume ($V$) é constante, la variação de volume ($\Delta V$) é zero:
$dV = 0$
e, nesse caso, la variação da energia interna ($dU$) é igual a o diferencial de calor impreciso ($\delta Q$):
$dU = \delta Q$
No caso de um gás, o estado depende de la temperatura absoluta ($T$), la pressão ($p$) e o volume ($V$). Portanto, se calor for adicionado, o aumento de temperatura dependerá se o volume ou a pressão são mantidos constantes. No primeiro caso, isso é chamado de la capacidade térmica em volume constante ($C_V$) e é denotado como $C_V$, e a relação é a seguinte:
| $ dU = C_V \Delta T $ |
Onde la capacidade térmica em volume constante ($C_V$) pode ser substituído por o calor específico dos gases a volume constante ($c_V$) e la massa ($M$) usando a seguinte relação:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Portanto, obtemos:
| $ dU = c_V M \Delta T $ |
ID:(11190, 0)
Aquecimento sob pressão constante
Descrição 
Se um gás é aquecido, a capacidade calorífica depende da forma como isso ocorre. Uma forma é a pressão constante, ou seja, permite-se que o volume se expanda ou contraia de modo que a pressão permaneça a mesma:
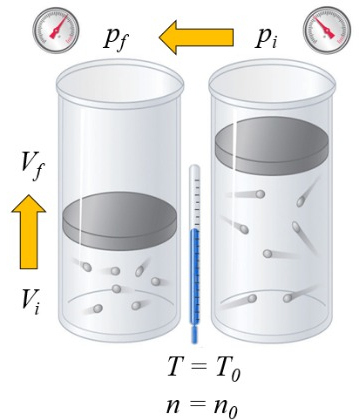
la capacidade calórica ($C$) em sólidos e líquidos pode ser considerado como uma constante $C$ que relaciona a variação de ERROR:8085 e ERROR:7510 por meio da equação:
| $ \Delta Q = C \Delta T $ |
No caso de um gás, o estado depende de la temperatura absoluta ($T$), la pressão ($p$) e o volume ($V$). Portanto, se calor for adicionado, o aumento de temperatura dependerá de se o volume ou a pressão são mantidos constantes. No primeiro caso, isso é chamado de la capacidade térmica a pressão constante ($C_p$) e é denotado como $C_p$, e a relação é a seguinte:
| $ \Delta Q = C_p \Delta T $ |
Onde la capacidade térmica a pressão constante ($C_p$) pode ser substituído por o calor específico a pressão constante ($c_p$) e la massa ($M$) usando a seguinte relação:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Portanto, obtemos:
| $ \Delta Q = c_p M \Delta T $ |
ID:(11189, 0)
Calorimetria em gases
Modelo 
A calorimetria é o processo de medição do calor associado a uma mudança em uma variável de estado. Essas variáveis de estado incluem tipicamente a temperatura, a pressão e o volume, embora outras possam ser incluídas dependendo do estado que está sendo descrito. Quando se mede a variação da temperatura em relação ao calor fornecido ou extraído, fala-se em capacidade térmica. No caso de um gás, a capacidade térmica é influenciada pelas demais variáveis de estado. Assim, a capacidade térmica é definida e medida a volume constante ou a pressão constante.
Variáveis
Cálculos
Cálculos
Equações
La capacidade calórica ($C$) em s lidos e l quidos pode ser considerado como uma constante $C$ que relaciona a varia o de la calor fornecido ao líquido ou sólido ($\Delta Q$) e ERROR:7510 por meio da equa o:
| $ \Delta Q = C \Delta T $ |
No caso em que o volume ($V$) constante, la variação de volume ($\Delta V$) zero:
$dV = 0$
e, nesse caso, la variação da energia interna ($dU$) igual a o diferencial de calor impreciso ($\delta Q$):
$dU = \delta Q$
No caso de um g s, o estado depende de la temperatura absoluta ($T$), la pressão ($p$) e o volume ($V$). Portanto, se calor for adicionado, o aumento de temperatura depender se o volume ou a press o s o mantidos constantes. No primeiro caso, isso chamado de la capacidade térmica em volume constante ($C_V$) e denotado como $C_V$, e a rela o a seguinte:
| $ dU = C_V \Delta T $ |
(ID 4862)
La capacidade calórica ($C$) em s lidos e l quidos pode ser considerado como uma constante $C$ que relaciona a varia o de ERROR:8085 e ERROR:7510 por meio da equa o:
| $ \Delta Q = C \Delta T $ |
No caso de um g s, o estado depende de la temperatura absoluta ($T$), la pressão ($p$) e o volume ($V$). Portanto, se calor for adicionado, o aumento de temperatura depender de se o volume ou a press o s o mantidos constantes. No primeiro caso, isso chamado de la capacidade térmica a pressão constante ($C_p$) e denotado como $C_p$, e a rela o a seguinte:
| $ \Delta Q = C_p \Delta T $ |
(ID 4863)
Seguindo uma analogia ao ERROR:5219,0 para l quidos e s lidos com la capacidade calórica ($C$) e la massa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe tamb m um calor específico dos gases a volume constante ($c_V$) para aquecimento a volume constante com la capacidade térmica em volume constante ($C_V$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
Seguindo uma analogia ao ERROR:5219,0 para l quidos e s lidos com la capacidade calórica ($C$) e la massa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe tamb m um calor específico a pressão constante ($c_p$) para o aquecimento a press o constante com la capacidade térmica a pressão constante ($C_p$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
(ID 11114)
La variação da energia interna ($dU$) em rela o a la variação de temperatura ($\Delta T$) e la capacidade térmica em volume constante ($C_V$) expresso da seguinte forma:
| $ dU = C_V \Delta T $ |
Onde la capacidade térmica em volume constante ($C_V$) pode ser substitu do por o calor específico dos gases a volume constante ($c_V$) e la massa ($M$) usando a seguinte rela o:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Portanto, obtemos:
| $ dU = c_V M \Delta T $ |
(ID 11115)
La calor fornecido ao líquido ou sólido ($\Delta Q$) em rela o a la variação de temperatura ($\Delta T$) e la capacidade térmica a pressão constante ($C_p$) expresso da seguinte forma:
| $ \Delta Q = C_p \Delta T $ |
Onde la capacidade térmica a pressão constante ($C_p$) pode ser substitu do por o calor específico a pressão constante ($c_p$) e la massa ($M$) usando a seguinte rela o:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Portanto, obtemos:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11116)
Exemplos
A calorimetria a ci ncia que mede a quantidade de calor envolvida em rea es qu micas, mudan as f sicas ou capacidade calor fica. Ela quantifica o calor trocado nos processos, fornecendo dados essenciais sobre as mudan as de energia envolvidas. A calorimetria determina a capacidade calor fica das subst ncias, indicando como diferentes materiais respondem ao calor. Tamb m mede as mudan as de entalpia nas rea es qu micas, mostrando se s o exot rmicas ou endot rmicas. Al m disso, a calorimetria estuda as transi es de fase, como fus o, ebuli o ou sublima o, medindo o calor absorvido ou liberado. Os dados obtidos da calorimetria podem ser usados para derivar outras propriedades termodin micas, como entropia e energia livre de Gibbs, oferecendo uma compreens o completa do comportamento de um sistema. O princ pio fundamental envolve o uso de um calor metro para medir com precis o a troca de calor atrav s do monitoramento das mudan as de temperatura, o que crucial em campos como qu mica, f sica, biologia e engenharia.
(ID 15244)
A convers o de trabalho em energia estudada atrav s da gera o de calor por meio do atrito. Para isso, envolve-se uma faixa met lica ao redor de um cilindro que cont m gua e um term metro. Ao girar a manivela, o atrito gera calor, levando ao aquecimento da gua. Se medirmos a for a aplicada, o n mero de voltas realizadas e o raio do cilindro, poss vel estimar a dist ncia percorrida, o que nos permite estimar a energia como o produto da for a pela dist ncia.

(ID 1884)
Se uma amostra a uma determinada temperatura for imersa em um copo de gua a uma temperatura mais baixa, observar-se- um aumento da temperatura da gua. Esse aumento depender da capacidade calor fica espec fica e da massa da amostra:

la calor fornecido ao líquido ou sólido ($\Delta Q$) est relacionado com la variação de temperatura ($\Delta T$) e la capacidade calórica ($C$) da seguinte forma:
| $ \Delta Q = C \Delta T $ |
Onde la capacidade calórica ($C$) pode ser substitu do por o calor específico ($c$) e la massa ($M$) usando a seguinte rela o:
| $ c =\displaystyle\frac{ C }{ M }$ |
Portanto, obtemos:
| $ \Delta Q = M c \Delta T$ |
(ID 15809)
Se um g s aquecido, a capacidade calor fica depende da forma como isso ocorre. Uma forma a volume constante, ou seja, o volume mantido fixo enquanto o sistema exposto a uma press o maior ou menor:

la capacidade calórica ($C$) em s lidos e l quidos pode ser considerado como uma constante $C$ que relaciona a varia o de la calor fornecido ao líquido ou sólido ($\Delta Q$) e ERROR:7510 por meio da equa o:
| $ \Delta Q = C \Delta T $ |
No caso em que o volume ($V$) constante, la variação de volume ($\Delta V$) zero:
$dV = 0$
e, nesse caso, la variação da energia interna ($dU$) igual a o diferencial de calor impreciso ($\delta Q$):
$dU = \delta Q$
No caso de um g s, o estado depende de la temperatura absoluta ($T$), la pressão ($p$) e o volume ($V$). Portanto, se calor for adicionado, o aumento de temperatura depender se o volume ou a press o s o mantidos constantes. No primeiro caso, isso chamado de la capacidade térmica em volume constante ($C_V$) e denotado como $C_V$, e a rela o a seguinte:
| $ dU = C_V \Delta T $ |
Onde la capacidade térmica em volume constante ($C_V$) pode ser substitu do por o calor específico dos gases a volume constante ($c_V$) e la massa ($M$) usando a seguinte rela o:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Portanto, obtemos:
| $ dU = c_V M \Delta T $ |
(ID 11190)
Se um g s aquecido, a capacidade calor fica depende da forma como isso ocorre. Uma forma a press o constante, ou seja, permite-se que o volume se expanda ou contraia de modo que a press o permane a a mesma:

la capacidade calórica ($C$) em s lidos e l quidos pode ser considerado como uma constante $C$ que relaciona a varia o de ERROR:8085 e ERROR:7510 por meio da equa o:
| $ \Delta Q = C \Delta T $ |
No caso de um g s, o estado depende de la temperatura absoluta ($T$), la pressão ($p$) e o volume ($V$). Portanto, se calor for adicionado, o aumento de temperatura depender de se o volume ou a press o s o mantidos constantes. No primeiro caso, isso chamado de la capacidade térmica a pressão constante ($C_p$) e denotado como $C_p$, e a rela o a seguinte:
| $ \Delta Q = C_p \Delta T $ |
Onde la capacidade térmica a pressão constante ($C_p$) pode ser substitu do por o calor específico a pressão constante ($c_p$) e la massa ($M$) usando a seguinte rela o:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Portanto, obtemos:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11189)
(ID 15303)
ID:(789, 0)
