Calorimétrie
Storyboard 
La calorimétrie est le processus de mesure de la chaleur associée à un changement d'une variable d'état. Ces variables d'état incluent typiquement la température, la pression et le volume, bien que d'autres puissent être incluses selon l'état décrit.
Lorsque la variation de température par rapport à la chaleur fournie ou extraite est mesurée, on parle de capacité calorifique. Dans le cas d'un gaz, la capacité calorifique est influencée par les autres variables d'état. Ainsi, la capacité calorifique est définie et mesurée à volume constant ou à pression constante.
ID:(789, 0)
Convertisseur travail-chaleur
Image 
La conversion du travail en énergie est étudiée en générant de la chaleur par frottement. Pour cela, on entoure un cylindre contenant de l'eau et un thermomètre d\'une bande métallique. En tournant la manivelle, la chaleur est générée par frottement, ce qui entraîne le réchauffement de l\'eau. Si l\'on mesure la force appliquée, le nombre de tours effectués et le rayon du cylindre, on peut estimer la distance parcourue, ce qui permet d\'estimer l\'énergie comme le produit de la force par la distance.

ID:(1884, 0)
Chauffage à volume constant
Citation 
Si un gaz est chauffé, la capacité calorifique dépend de la manière dont cela se produit. Une façon est à volume constant, c'est-à-dire que le volume est maintenu fixe tandis que le système est exposé à une pression plus élevée ou plus basse:
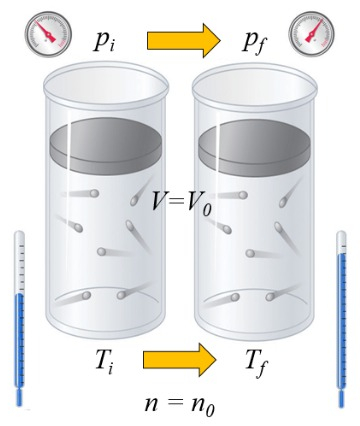
a capacité calorique ($C$) dans les solides et les liquides peut être considéré comme une constante $C$ qui relie la variation de a chaleur fournie au liquide ou au solide ($\Delta Q$) et ERROR:7510 à travers l'équation :
| $ \Delta Q = C \Delta T $ |
Dans le cas où Le volume ($V$) est constant, a variation de volume ($\Delta V$) est nul:
$dV = 0$
et dans ce cas, a variation de l'énergie interne ($dU$) est égal à Le différence de chaleur inexacte ($\delta Q$):
$dU = \delta Q$
Dans le cas d'un gaz, l'état dépend de a température absolue ($T$), a pression ($p$), et le volume ($V$). Par conséquent, si de la chaleur est ajoutée, l'augmentation de température dépendra de la constance du volume ou de la pression. Dans le premier cas, on parle de a capacité thermique à volume constant ($C_V$) et on le note $C_V$, et la relation est la suivante :
| $ dU = C_V \Delta T $ |
Où A capacité thermique à volume constant ($C_V$) peut être remplacé par le chaleur spécifique des gaz à volume constant ($c_V$) et a masse ($M$) en utilisant la relation suivante :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Par conséquent, nous obtenons :
| $ dU = c_V M \Delta T $ |
ID:(11190, 0)
Chauffage sous pression constante
Exercer 
Si un gaz est chauffé, la capacité calorifique dépend de la manière dont cela se produit. Une façon est à pression constante, c'est-à-dire que le volume est autorisé à se dilater ou à se contracter de manière à ce que la pression reste constante:
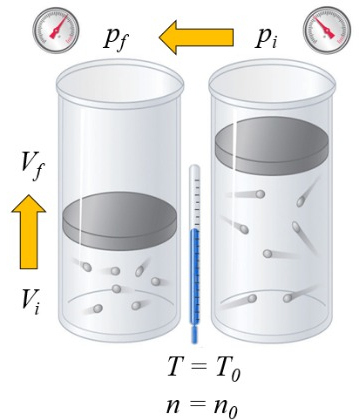
a capacité calorique ($C$) dans les solides et les liquides peut être considéré comme une constante $C$ qui relie la variation de ERROR:8085 et ERROR:7510 à travers l'équation :
| $ \Delta Q = C \Delta T $ |
Dans le cas d'un gaz, l'état dépend de a température absolue ($T$), a pression ($p$), et le volume ($V$). Par conséquent, si de la chaleur est ajoutée, l'augmentation de température dépendra de si le volume ou la pression est maintenu constant. Dans le premier cas, on parle de a capacité thermique à pression constante ($C_p$) et on le note $C_p$, et la relation est la suivante :
| $ \Delta Q = C_p \Delta T $ |
Où A capacité thermique à pression constante ($C_p$) peut être remplacé par le chaleur spécifique à pression constante ($c_p$) et a masse ($M$) en utilisant la relation suivante :
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Par conséquent, nous obtenons :
| $ \Delta Q = c_p M \Delta T $ |
ID:(11189, 0)
Calorimétrie dans les gaz
Description 
La calorimétrie est le processus de mesure de la chaleur associée à un changement d'une variable d'état. Ces variables d'état incluent typiquement la température, la pression et le volume, bien que d'autres puissent être incluses selon l'état décrit. Lorsque la variation de température par rapport à la chaleur fournie ou extraite est mesurée, on parle de capacité calorifique. Dans le cas d'un gaz, la capacité calorifique est influencée par les autres variables d'état. Ainsi, la capacité calorifique est définie et mesurée à volume constant ou à pression constante.
Variables
Calculs
Calculs
Équations
A capacité calorique ($C$) dans les solides et les liquides peut tre consid r comme une constante $C$ qui relie la variation de a chaleur fournie au liquide ou au solide ($\Delta Q$) et ERROR:7510 travers l' quation :
| $ \Delta Q = C \Delta T $ |
Dans le cas o le volume ($V$) est constant, a variation de volume ($\Delta V$) est nul:
$dV = 0$
et dans ce cas, a variation de l'énergie interne ($dU$) est gal le différence de chaleur inexacte ($\delta Q$):
$dU = \delta Q$
Dans le cas d'un gaz, l' tat d pend de a température absolue ($T$), a pression ($p$), et le volume ($V$). Par cons quent, si de la chaleur est ajout e, l'augmentation de temp rature d pendra de la constance du volume ou de la pression. Dans le premier cas, on parle de a capacité thermique à volume constant ($C_V$) et on le note $C_V$, et la relation est la suivante :
| $ dU = C_V \Delta T $ |
(ID 4862)
A capacité calorique ($C$) dans les solides et les liquides peut tre consid r comme une constante $C$ qui relie la variation de ERROR:8085 et ERROR:7510 travers l' quation :
| $ \Delta Q = C \Delta T $ |
Dans le cas d'un gaz, l' tat d pend de a température absolue ($T$), a pression ($p$), et le volume ($V$). Par cons quent, si de la chaleur est ajout e, l'augmentation de temp rature d pendra de si le volume ou la pression est maintenu constant. Dans le premier cas, on parle de a capacité thermique à pression constante ($C_p$) et on le note $C_p$, et la relation est la suivante :
| $ \Delta Q = C_p \Delta T $ |
(ID 4863)
En suivant une analogie avec le ERROR:5219,0 pour les liquides et les solides avec a capacité calorique ($C$) et a masse ($M$) :
| $ c =\displaystyle\frac{ C }{ M }$ |
il existe galement un chaleur spécifique des gaz à volume constant ($c_V$) pour le chauffage volume constant avec a capacité thermique à volume constant ($C_V$) :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
En suivant une analogie avec le ERROR:5219,0 pour les liquides et les solides avec a capacité calorique ($C$) et a masse ($M$) :
| $ c =\displaystyle\frac{ C }{ M }$ |
il existe galement un chaleur spécifique à pression constante ($c_p$) pour le chauffage pression constante avec a capacité thermique à pression constante ($C_p$) :
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
(ID 11114)
A variation de l'énergie interne ($dU$) par rapport a variation de température ($\Delta T$) et a capacité thermique à volume constant ($C_V$) s'exprime comme suit :
| $ dU = C_V \Delta T $ |
O A capacité thermique à volume constant ($C_V$) peut tre remplac par le chaleur spécifique des gaz à volume constant ($c_V$) et a masse ($M$) en utilisant la relation suivante :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Par cons quent, nous obtenons :
| $ dU = c_V M \Delta T $ |
(ID 11115)
A chaleur fournie au liquide ou au solide ($\Delta Q$) par rapport a variation de température ($\Delta T$) et a capacité thermique à pression constante ($C_p$) s'exprime comme suit :
| $ \Delta Q = C_p \Delta T $ |
O A capacité thermique à pression constante ($C_p$) peut tre remplac par le chaleur spécifique à pression constante ($c_p$) et a masse ($M$) en utilisant la relation suivante :
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Par cons quent, nous obtenons :
| $ \Delta Q = c_p M \Delta T $ |
(ID 11116)
Exemples
La calorim trie est la science qui mesure la quantit de chaleur impliqu e dans les r actions chimiques, les changements physiques ou la capacit calorifique. Elle quantifie la chaleur chang e dans les processus, fournissant des donn es essentielles sur les changements d' nergie impliqu s. La calorim trie d termine la capacit calorifique des substances, indiquant comment diff rents mat riaux r agissent la chaleur. Elle mesure galement les changements d'enthalpie dans les r actions chimiques, montrant si elles sont exothermiques ou endothermiques. De plus, la calorim trie tudie les transitions de phase telles que la fusion, l' bullition ou la sublimation en mesurant la chaleur absorb e ou lib r e. Les donn es obtenues de la calorim trie peuvent tre utilis es pour d river d'autres propri t s thermodynamiques comme l'entropie et l' nergie libre de Gibbs, offrant une compr hension compl te du comportement d'un syst me. Le principe fondamental implique l'utilisation d'un calorim tre pour mesurer avec pr cision l' change de chaleur en surveillant les changements de temp rature, ce qui est crucial dans des domaines comme la chimie, la physique, la biologie et l'ing nierie.
(ID 15244)
La conversion du travail en nergie est tudi e en g n rant de la chaleur par frottement. Pour cela, on entoure un cylindre contenant de l'eau et un thermom tre d\'une bande m tallique. En tournant la manivelle, la chaleur est g n r e par frottement, ce qui entra ne le r chauffement de l\'eau. Si l\'on mesure la force appliqu e, le nombre de tours effectu s et le rayon du cylindre, on peut estimer la distance parcourue, ce qui permet d\'estimer l\' nergie comme le produit de la force par la distance.

(ID 1884)
Si une chantillon une temp rature donn e est immerg dans un verre d'eau une temp rature plus basse, une augmentation de la temp rature de l'eau sera observ e. Cette augmentation d pendra de la capacit calorifique sp cifique et de la masse de l' chantillon:
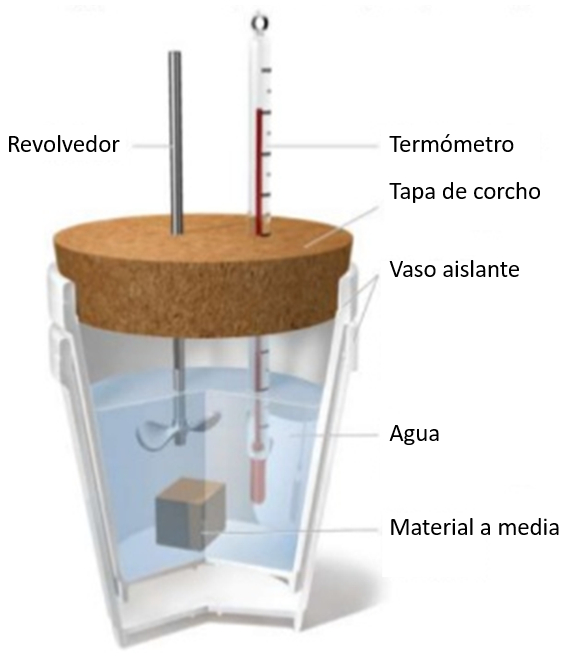
a chaleur fournie au liquide ou au solide ($\Delta Q$) est li a variation de température ($\Delta T$) et a capacité calorique ($C$) comme suit :
| $ \Delta Q = C \Delta T $ |
O A capacité calorique ($C$) peut tre remplac par le chaleur spécifique ($c$) et a masse ($M$) en utilisant la relation suivante :
| $ c =\displaystyle\frac{ C }{ M }$ |
Par cons quent, nous obtenons :
| $ \Delta Q = M c \Delta T$ |
(ID 15809)
Si un gaz est chauff , la capacit calorifique d pend de la mani re dont cela se produit. Une fa on est volume constant, c'est- -dire que le volume est maintenu fixe tandis que le syst me est expos une pression plus lev e ou plus basse:

a capacité calorique ($C$) dans les solides et les liquides peut tre consid r comme une constante $C$ qui relie la variation de a chaleur fournie au liquide ou au solide ($\Delta Q$) et ERROR:7510 travers l' quation :
| $ \Delta Q = C \Delta T $ |
Dans le cas o le volume ($V$) est constant, a variation de volume ($\Delta V$) est nul:
$dV = 0$
et dans ce cas, a variation de l'énergie interne ($dU$) est gal le différence de chaleur inexacte ($\delta Q$):
$dU = \delta Q$
Dans le cas d'un gaz, l' tat d pend de a température absolue ($T$), a pression ($p$), et le volume ($V$). Par cons quent, si de la chaleur est ajout e, l'augmentation de temp rature d pendra de la constance du volume ou de la pression. Dans le premier cas, on parle de a capacité thermique à volume constant ($C_V$) et on le note $C_V$, et la relation est la suivante :
| $ dU = C_V \Delta T $ |
O A capacité thermique à volume constant ($C_V$) peut tre remplac par le chaleur spécifique des gaz à volume constant ($c_V$) et a masse ($M$) en utilisant la relation suivante :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Par cons quent, nous obtenons :
| $ dU = c_V M \Delta T $ |
(ID 11190)
Si un gaz est chauff , la capacit calorifique d pend de la mani re dont cela se produit. Une fa on est pression constante, c'est- -dire que le volume est autoris se dilater ou se contracter de mani re ce que la pression reste constante:

a capacité calorique ($C$) dans les solides et les liquides peut tre consid r comme une constante $C$ qui relie la variation de ERROR:8085 et ERROR:7510 travers l' quation :
| $ \Delta Q = C \Delta T $ |
Dans le cas d'un gaz, l' tat d pend de a température absolue ($T$), a pression ($p$), et le volume ($V$). Par cons quent, si de la chaleur est ajout e, l'augmentation de temp rature d pendra de si le volume ou la pression est maintenu constant. Dans le premier cas, on parle de a capacité thermique à pression constante ($C_p$) et on le note $C_p$, et la relation est la suivante :
| $ \Delta Q = C_p \Delta T $ |
O A capacité thermique à pression constante ($C_p$) peut tre remplac par le chaleur spécifique à pression constante ($c_p$) et a masse ($M$) en utilisant la relation suivante :
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Par cons quent, nous obtenons :
| $ \Delta Q = c_p M \Delta T $ |
(ID 11189)
(ID 15303)
ID:(789, 0)
