User:
Calorimetry in gases
Storyboard 
Calorimetry is the process of measuring the heat associated with a change in a state variable. These state variables typically include temperature, pressure, and volume, though others may be included depending on the state being described.
When the variation in temperature relative to the heat supplied or extracted is measured, it is referred to as heat capacity. In the case of a gas, the heat capacity is influenced by the other state variables. Therefore, heat capacity is defined and measured at constant volume or constant pressure.
ID:(789, 0)
Mechanisms
Iframe
Calorimetry is the science of measuring the amount of heat involved in chemical reactions, physical changes, or heat capacity. It quantifies the heat exchanged in processes, providing essential data on the energy changes involved. Calorimetry determines the heat capacity of substances, indicating how different materials respond to heat. It also measures enthalpy changes in chemical reactions, showing whether they are exothermic or endothermic. Additionally, calorimetry studies phase transitions such as melting, boiling, or sublimation by measuring the heat absorbed or released. The data obtained from calorimetry can be used to derive other thermodynamic properties like entropy and Gibbs free energy, offering a comprehensive understanding of a system's behavior. The core principle involves using a calorimeter to measure heat exchange accurately by monitoring temperature changes, which is crucial in fields like chemistry, physics, biology, and engineering.
Mechanisms
ID:(15244, 0)
Working converter heat
Description
The conversion of work into energy is studied by generating heat through friction. To do this, a metal band is wrapped around a cylinder containing water and a thermometer. By turning the crank, heat is generated through friction, leading to the heating of the water. If the applied force, the number of rotations, and the radius of the cylinder are measured, the distance traveled can be estimated, allowing for the estimation of energy as the product of force and distance.
ID:(1884, 0)
Calorie content of a solid and liquid
Concept
If a sample at a given temperature is immersed in a glass of water at a lower temperature, an increase in the water's temperature will be observed. This increase will depend on the specific heat capacity and the mass of the sample:
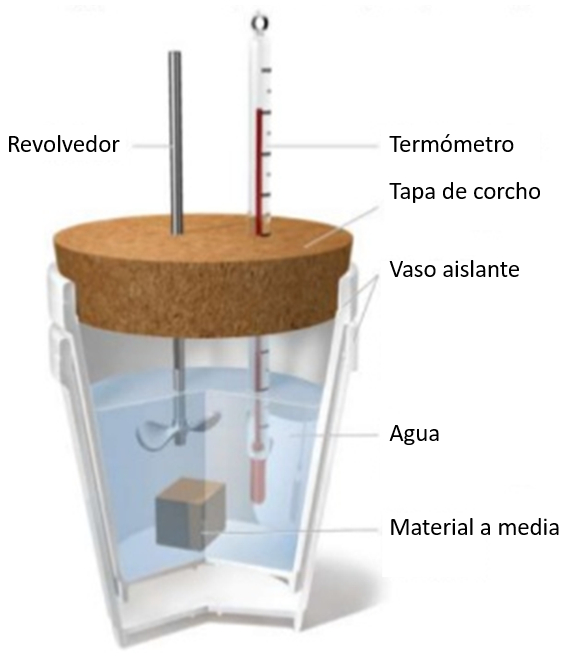
the heat supplied to liquid or solid ($\Delta Q$) is related to the temperature variation in a liquid or solid ($\Delta T$) and the heat capacity ($C$) as follows:
| $ \Delta Q = C \Delta T $ |
Where the heat capacity ($C$) can be replaced by the specific heat ($c$) and the mass ($M$) using the following relationship:
| $ c =\displaystyle\frac{ C }{ M }$ |
Therefore, we obtain:
| $ \Delta Q = M c \Delta T$ |
ID:(15809, 0)
Heating under constant volume
Description
If a gas is heated, the heat capacity depends on the way this occurs. One way is at constant volume, meaning the volume is kept fixed while the system is exposed to a higher or lower pressure:
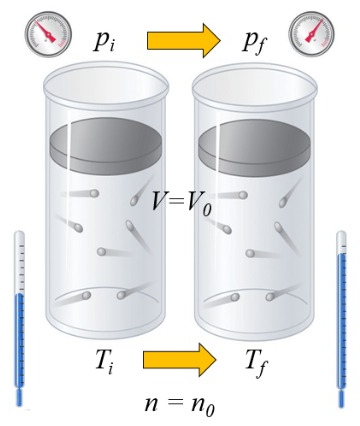
the heat capacity ($C$) in solids and liquids can be considered as a constant $C$ that relates the change in the heat supplied to liquid or solid ($\Delta Q$) and the variación de Temperature ($\Delta T$) through the equation:
| $ \Delta Q = C \Delta T $ |
In the case where the volume ($V$) is constant, the volume Variation ($dV$) is zero:
$dV = 0$
and in this case, the variation of the internal energy ($dU$) is equal to the differential inexact Heat ($\delta Q$):
$dU = \delta Q$
In the case of a gas, the state depends on the absolute temperature ($T$), the pressure ($p$), and the volume ($V$). Therefore, if heat is added, the increase in temperature will depend on whether the volume or the pressure is held constant. In the first case, it is referred to as the heat capacity at constant volume ($C_V$) and denoted as $C_V$, and the relationship is as follows:
| $ dU = C_V \Delta T $ |
Where the heat capacity at constant volume ($C_V$) can be replaced by the specific heat of gases at constant volume ($c_V$) and the mass ($M$) using the following relationship:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Therefore, we obtain:
| $ dU = c_V M \Delta T $ |
ID:(11190, 0)
Heating under constant pressure
Description
If a gas is heated, the heat capacity depends on the way this occurs. One way is at constant pressure, where the volume is allowed to expand or contract in such a way that the pressure remains constant:
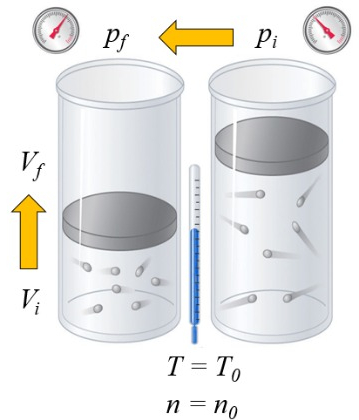
the heat capacity ($C$) in solids and liquids can be considered as a constant $C$ that relates the change in ($$) and the variación de Temperature ($\Delta T$) through the equation:
| $ \Delta Q = C \Delta T $ |
In the case of a gas, the state depends on the absolute temperature ($T$), the pressure ($p$), and the volume ($V$). Therefore, if heat is added, the increase in temperature will depend on whether the volume or the pressure is held constant. In the first case, it is referred to as the heat capacity at constant pressure ($C_p$) and denoted as $C_p$, and the relationship is as follows:
| $ \Delta Q = C_p \Delta T $ |
Where the heat capacity at constant pressure ($C_p$) can be replaced by the specific heat at constant pressure ($c_p$) and the mass ($M$) using the following relationship:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Therefore, we obtain:
| $ \Delta Q = c_p M \Delta T $ |
ID:(11189, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ c_p =\displaystyle\frac{ C_p }{ M }$
c_p = C_p / M
$ c_V =\displaystyle\frac{ C_V }{ M }$
c_V = C_V / M
$ \Delta Q = C_p \Delta T $
DQ = C_p * DT
$ \Delta Q = c_p M \Delta T $
DQ = c_p * M * DT
$ dU = C_V \Delta T $
dU = C_V * DT
$ dU = c_V M \Delta T $
dU = c_V * M * DT
ID:(15303, 0)
Caloric content of a gas at a constant volume
Equation
The variation of the internal energy ($dU$) is for the case that the volume ($V$) is constant equal to the heat capacity at constant volume ($C_V$) for the absolute temperature ($T$):
| $ dU = C_V \Delta T $ |
The heat capacity ($C$) in solids and liquids can be considered as a constant $C$ that relates the change in the heat supplied to liquid or solid ($\Delta Q$) and the variación de Temperature ($\Delta T$) through the equation:
| $ \Delta Q = C \Delta T $ |
In the case where the volume ($V$) is constant, the volume Variation ($dV$) is zero:
$dV = 0$
and in this case, the variation of the internal energy ($dU$) is equal to the differential inexact Heat ($\delta Q$):
$dU = \delta Q$
In the case of a gas, the state depends on the absolute temperature ($T$), the pressure ($p$), and the volume ($V$). Therefore, if heat is added, the increase in temperature will depend on whether the volume or the pressure is held constant. In the first case, it is referred to as the heat capacity at constant volume ($C_V$) and denoted as $C_V$, and the relationship is as follows:
| $ dU = C_V \Delta T $ |
ID:(4862, 0)
Calorie content of a constant pressure gas
Equation
($$) can be calculated from the heat capacity at constant pressure ($C_p$) and the variación de Temperature ($\Delta T$) using:
| $ \Delta Q = C_p \Delta T $ |
The heat capacity ($C$) in solids and liquids can be considered as a constant $C$ that relates the change in ($$) and the variación de Temperature ($\Delta T$) through the equation:
| $ \Delta Q = C \Delta T $ |
In the case of a gas, the state depends on the absolute temperature ($T$), the pressure ($p$), and the volume ($V$). Therefore, if heat is added, the increase in temperature will depend on whether the volume or the pressure is held constant. In the first case, it is referred to as the heat capacity at constant pressure ($C_p$) and denoted as $C_p$, and the relationship is as follows:
| $ \Delta Q = C_p \Delta T $ |
ID:(4863, 0)
Specific heat of gases at constant volume
Equation
The specific heat of gases at constant volume ($c_V$) is equal to the heat capacity at constant volume ($C_V$) divided by the mass ($M$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Continuing the analogy to the specific heat ($c$) for liquids and solids with the heat capacity ($C$) and the mass ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
there is also a specific heat of gases at constant volume ($c_V$) for heating at constant volume with the heat capacity at constant volume ($C_V$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
ID:(11113, 0)
Caloric content of a gas at constant volume as a function of specific heat
Equation
The relationship between the variation of the variation of the internal energy ($dU$) and the temperature variation in a liquid or solid ($\Delta T$) is with the specific heat of gases at constant volume ($c_V$) and the mass ($M$) equal to:
| $ dU = c_V M \Delta T $ |
The variation of the internal energy ($dU$) in relation to the temperature variation in a liquid or solid ($\Delta T$) and the heat capacity at constant volume ($C_V$) is expressed as:
| $ dU = C_V \Delta T $ |
Where the heat capacity at constant volume ($C_V$) can be replaced by the specific heat of gases at constant volume ($c_V$) and the mass ($M$) using the following relationship:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Therefore, we obtain:
| $ dU = c_V M \Delta T $ |
ID:(11115, 0)
Specific heat of gases at constant pressure
Equation
The specific heat at constant pressure ($c_p$) is equal to the heat capacity at constant pressure ($C_p$) divided by the mass ($M$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Following an analogy to the specific heat ($c$) for liquids and solids with the heat capacity ($C$) and the mass ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
there is also a specific heat at constant pressure ($c_p$) for heating at constant pressure with the heat capacity at constant pressure ($C_p$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
ID:(11114, 0)
Caloric content of a gas at constant pressure as a function of specific heat
Equation
The heat supplied to liquid or solid ($\Delta Q$) can be calculated with the specific heat at constant pressure ($c_p$), the mass ($M$) and the temperature variation in a liquid or solid ($\Delta T$) using:
| $ \Delta Q = c_p M \Delta T $ |
The heat supplied to liquid or solid ($\Delta Q$) in relation to the temperature variation in a liquid or solid ($\Delta T$) and the heat capacity at constant pressure ($C_p$) is expressed as:
| $ \Delta Q = C_p \Delta T $ |
Where the heat capacity at constant pressure ($C_p$) can be replaced by the specific heat at constant pressure ($c_p$) and the mass ($M$) using the following relationship:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Therefore, we obtain:
| $ \Delta Q = c_p M \Delta T $ |
ID:(11116, 0)