Kalorimetrie
Storyboard 
Die Kalorimetrie ist der Prozess der Messung der Wärme, die mit einer Änderung einer Zustandsvariablen verbunden ist. Diese Zustandsvariablen umfassen typischerweise die Temperatur, den Druck und das Volumen, können aber je nach zu beschreibendem Zustand auch andere einschließen.
Wenn die Variation der Temperatur in Bezug auf die zugeführte oder entzogene Wärme gemessen wird, spricht man von der Wärmekapazität. Im Falle eines Gases wird die Wärmekapazität von den anderen Zustandsvariablen beeinflusst. Daher wird die Wärmekapazität bei konstantem Volumen oder konstantem Druck definiert und gemessen.
ID:(789, 0)
Umwandlung von Arbeit in Wärme
Bild 
Die Umwandlung von Arbeit in Energie wird durch die Erzeugung von Wärme durch Reibung untersucht. Dazu wird ein Metallband um einen Zylinder gewickelt, der Wasser und ein Thermometer enthält. Durch Drehen der Kurbel entsteht durch Reibung Wärme, die zur Erwärmung des Wassers führt. Wenn die aufgebrachte Kraft, die Anzahl der Umdrehungen und der Radius des Zylinders gemessen werden, kann die zurückgelegte Strecke geschätzt werden, was wiederum die Energie als das Produkt aus Kraft und Strecke ermöglicht.

ID:(1884, 0)
Erhitzen unter konstantem Volumen
Zitat 
Wenn ein Gas erhitzt wird, hängt die Wärmekapazität davon ab, wie dies geschieht. Eine Möglichkeit besteht darin, das Volumen konstant zu halten, d.h. das Volumen bleibt festgelegt, während das System einem höheren oder niedrigeren Druck ausgesetzt wird:
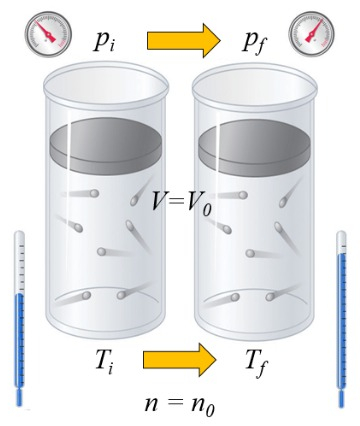
die Wärmekapazität ($C$) in Feststoffen und Flüssigkeiten kann als eine Konstante $C$ betrachtet werden, die die Änderung von die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) und die Variación de Temperature ($\Delta T$) durch die Gleichung verknüpft:
| $ \Delta Q = C \Delta T $ |
Im Fall, dass der Volumen ($V$) konstant ist, ist die Volumenvariation ($\Delta V$) gleich null:
$dV = 0$
und in diesem Fall ist die Änderung der inneren Energie ($dU$) gleich der Differential ungenau Wärme ($\delta Q$):
$dU = \delta Q$
Im Fall eines Gases hängt der Zustand von die Absolute Temperatur ($T$), die Druck ($p$) und der Volumen ($V$) ab. Daher hängt die Temperaturerhöhung davon ab, ob das Volumen oder der Druck konstant gehalten wird, wenn Wärme hinzugefügt wird. Im ersten Fall spricht man von die Wärmekapazität bei konstantem Volumen ($C_V$) und bezeichnet es als $C_V$, und die Beziehung lautet wie folgt:
| $ dU = C_V \Delta T $ |
Wobei die Wärmekapazität bei konstantem Volumen ($C_V$) durch der Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$) und die Masse ($M$) gemäß folgender Beziehung ersetzt werden kann:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Daher erhalten wir:
| $ dU = c_V M \Delta T $ |
ID:(11190, 0)
Heizung unter konstantem Druck
Übung 
Wenn ein Gas erhitzt wird, hängt die Wärmekapazität davon ab, wie dies geschieht. Eine Möglichkeit ist bei konstantem Druck, bei der das Volumen so verändert wird, dass der Druck konstant bleibt:
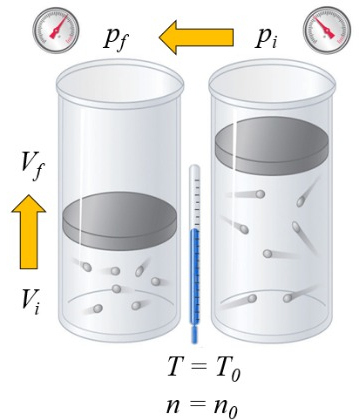
die Wärmekapazität ($C$) in Feststoffen und Flüssigkeiten kann als eine Konstante $C$ betrachtet werden, die die Änderung von ERROR:8085 und die Variación de Temperature ($\Delta T$) durch die Gleichung verknüpft:
| $ \Delta Q = C \Delta T $ |
Im Fall eines Gases hängt der Zustand von die Absolute Temperatur ($T$), die Druck ($p$) und der Volumen ($V$) ab. Daher hängt die Temperaturerhöhung davon ab, ob das Volumen oder der Druck konstant gehalten wird, wenn Wärme hinzugefügt wird. Im ersten Fall spricht man von die Wärmekapazität bei konstantem Druck ($C_p$) und bezeichnet es als $C_p$, und die Beziehung lautet wie folgt:
| $ \Delta Q = C_p \Delta T $ |
Wobei die Wärmekapazität bei konstantem Druck ($C_p$) durch der Spezifische Wärme bei konstantem Druck ($c_p$) und die Masse ($M$) gemäß folgender Beziehung ersetzt werden kann:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Daher erhalten wir:
| $ \Delta Q = c_p M \Delta T $ |
ID:(11189, 0)
Kalorimetrie in Gasen
Beschreibung 
Die Kalorimetrie ist der Prozess der Messung der Wärme, die mit einer Änderung einer Zustandsvariablen verbunden ist. Diese Zustandsvariablen umfassen typischerweise die Temperatur, den Druck und das Volumen, können aber je nach zu beschreibendem Zustand auch andere einschließen. Wenn die Variation der Temperatur in Bezug auf die zugeführte oder entzogene Wärme gemessen wird, spricht man von der Wärmekapazität. Im Falle eines Gases wird die Wärmekapazität von den anderen Zustandsvariablen beeinflusst. Daher wird die Wärmekapazität bei konstantem Volumen oder konstantem Druck definiert und gemessen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Wärmekapazität ($C$) in Feststoffen und Fl ssigkeiten kann als eine Konstante $C$ betrachtet werden, die die nderung von die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) und die Variación de Temperature ($\Delta T$) durch die Gleichung verkn pft:
| $ \Delta Q = C \Delta T $ |
Im Fall, dass der Volumen ($V$) konstant ist, ist die Volumenvariation ($\Delta V$) gleich null:
$dV = 0$
und in diesem Fall ist die Änderung der inneren Energie ($dU$) gleich der Differential ungenau Wärme ($\delta Q$):
$dU = \delta Q$
Im Fall eines Gases h ngt der Zustand von die Absolute Temperatur ($T$), die Druck ($p$) und der Volumen ($V$) ab. Daher h ngt die Temperaturerh hung davon ab, ob das Volumen oder der Druck konstant gehalten wird, wenn W rme hinzugef gt wird. Im ersten Fall spricht man von die Wärmekapazität bei konstantem Volumen ($C_V$) und bezeichnet es als $C_V$, und die Beziehung lautet wie folgt:
| $ dU = C_V \Delta T $ |
(ID 4862)
Die Wärmekapazität ($C$) in Feststoffen und Fl ssigkeiten kann als eine Konstante $C$ betrachtet werden, die die nderung von ERROR:8085 und die Variación de Temperature ($\Delta T$) durch die Gleichung verkn pft:
| $ \Delta Q = C \Delta T $ |
Im Fall eines Gases h ngt der Zustand von die Absolute Temperatur ($T$), die Druck ($p$) und der Volumen ($V$) ab. Daher h ngt die Temperaturerh hung davon ab, ob das Volumen oder der Druck konstant gehalten wird, wenn W rme hinzugef gt wird. Im ersten Fall spricht man von die Wärmekapazität bei konstantem Druck ($C_p$) und bezeichnet es als $C_p$, und die Beziehung lautet wie folgt:
| $ \Delta Q = C_p \Delta T $ |
(ID 4863)
Folgend einer Analogie zum ERROR:5219,0 f r Fl ssigkeiten und Feststoffe mit die Wärmekapazität ($C$) und die Masse ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
gibt es auch ein Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$) f r das Erhitzen bei konstantem Volumen mit die Wärmekapazität bei konstantem Volumen ($C_V$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
In Anlehnung an die Analogie zum ERROR:5219,0 f r Fl ssigkeiten und Feststoffe mit die Wärmekapazität ($C$) und die Masse ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
gibt es auch ein Spezifische Wärme bei konstantem Druck ($c_p$) f r das Erw rmen bei konstantem Druck mit die Wärmekapazität bei konstantem Druck ($C_p$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
(ID 11114)
Die Änderung der inneren Energie ($dU$) in Bezug auf die Temperaturschwankungen ($\Delta T$) und die Wärmekapazität bei konstantem Volumen ($C_V$) wird wie folgt ausgedr ckt:
| $ dU = C_V \Delta T $ |
Wobei die Wärmekapazität bei konstantem Volumen ($C_V$) durch der Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$) und die Masse ($M$) gem folgender Beziehung ersetzt werden kann:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Daher erhalten wir:
| $ dU = c_V M \Delta T $ |
(ID 11115)
Die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) in Bezug auf die Temperaturschwankungen ($\Delta T$) und die Wärmekapazität bei konstantem Druck ($C_p$) wird wie folgt ausgedr ckt:
| $ \Delta Q = C_p \Delta T $ |
Wobei die Wärmekapazität bei konstantem Druck ($C_p$) durch der Spezifische Wärme bei konstantem Druck ($c_p$) und die Masse ($M$) gem folgender Beziehung ersetzt werden kann:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Daher erhalten wir:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11116)
Beispiele
Die Kalorimetrie ist die Wissenschaft, die sich mit der Messung der W rmemenge befasst, die bei chemischen Reaktionen, physikalischen Ver nderungen oder der W rmekapazit t beteiligt ist. Sie quantifiziert den W rmeaustausch in Prozessen und liefert wesentliche Daten ber die dabei auftretenden Energie nderungen. Die Kalorimetrie bestimmt die W rmekapazit t von Substanzen und zeigt, wie verschiedene Materialien auf W rme reagieren. Sie misst auch die Enthalpie nderungen bei chemischen Reaktionen und zeigt, ob diese exotherm oder endotherm sind. Zudem untersucht die Kalorimetrie Phasen berg nge wie Schmelzen, Sieden oder Sublimieren, indem sie die aufgenommene oder abgegebene W rme misst. Die aus der Kalorimetrie gewonnenen Daten k nnen verwendet werden, um andere thermodynamische Eigenschaften wie Entropie und Gibbs'sche freie Energie abzuleiten, was ein umfassendes Verst ndnis des Verhaltens eines Systems bietet. Das grundlegende Prinzip beinhaltet die Verwendung eines Kalorimeters, um den W rmeaustausch durch berwachung der Temperatur nderungen genau zu messen, was in Bereichen wie Chemie, Physik, Biologie und Ingenieurwesen von entscheidender Bedeutung ist.
(ID 15244)
Die Umwandlung von Arbeit in Energie wird durch die Erzeugung von W rme durch Reibung untersucht. Dazu wird ein Metallband um einen Zylinder gewickelt, der Wasser und ein Thermometer enth lt. Durch Drehen der Kurbel entsteht durch Reibung W rme, die zur Erw rmung des Wassers f hrt. Wenn die aufgebrachte Kraft, die Anzahl der Umdrehungen und der Radius des Zylinders gemessen werden, kann die zur ckgelegte Strecke gesch tzt werden, was wiederum die Energie als das Produkt aus Kraft und Strecke erm glicht.

(ID 1884)
Wenn eine Probe bei einer bestimmten Temperatur in ein Glas Wasser mit niedrigerer Temperatur eingetaucht wird, wird ein Temperaturanstieg des Wassers beobachtet. Dieser Anstieg h ngt von der spezifischen W rmekapazit t und der Masse der Probe ab:
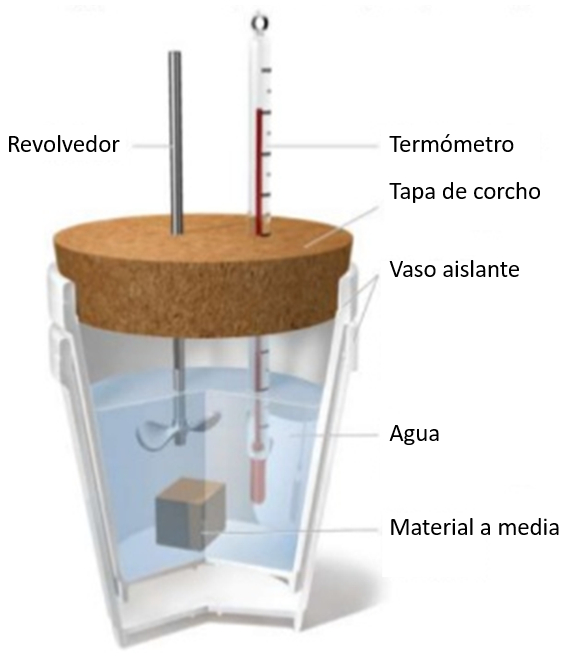
die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) ist in Beziehung zu die Temperaturschwankungen ($\Delta T$) und die Wärmekapazität ($C$) wie folgt:
| $ \Delta Q = C \Delta T $ |
Wobei die Wärmekapazität ($C$) durch der Spezifische Wärme ($c$) und die Masse ($M$) gem folgender Beziehung ersetzt werden kann:
| $ c =\displaystyle\frac{ C }{ M }$ |
Daher erhalten wir:
| $ \Delta Q = M c \Delta T$ |
(ID 15809)
Wenn ein Gas erhitzt wird, h ngt die W rmekapazit t davon ab, wie dies geschieht. Eine M glichkeit besteht darin, das Volumen konstant zu halten, d.h. das Volumen bleibt festgelegt, w hrend das System einem h heren oder niedrigeren Druck ausgesetzt wird:

die Wärmekapazität ($C$) in Feststoffen und Fl ssigkeiten kann als eine Konstante $C$ betrachtet werden, die die nderung von die Der Flüssigkeit oder dem Feststoff zugeführte Wärme ($\Delta Q$) und die Variación de Temperature ($\Delta T$) durch die Gleichung verkn pft:
| $ \Delta Q = C \Delta T $ |
Im Fall, dass der Volumen ($V$) konstant ist, ist die Volumenvariation ($\Delta V$) gleich null:
$dV = 0$
und in diesem Fall ist die Änderung der inneren Energie ($dU$) gleich der Differential ungenau Wärme ($\delta Q$):
$dU = \delta Q$
Im Fall eines Gases h ngt der Zustand von die Absolute Temperatur ($T$), die Druck ($p$) und der Volumen ($V$) ab. Daher h ngt die Temperaturerh hung davon ab, ob das Volumen oder der Druck konstant gehalten wird, wenn W rme hinzugef gt wird. Im ersten Fall spricht man von die Wärmekapazität bei konstantem Volumen ($C_V$) und bezeichnet es als $C_V$, und die Beziehung lautet wie folgt:
| $ dU = C_V \Delta T $ |
Wobei die Wärmekapazität bei konstantem Volumen ($C_V$) durch der Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$) und die Masse ($M$) gem folgender Beziehung ersetzt werden kann:
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Daher erhalten wir:
| $ dU = c_V M \Delta T $ |
(ID 11190)
Wenn ein Gas erhitzt wird, h ngt die W rmekapazit t davon ab, wie dies geschieht. Eine M glichkeit ist bei konstantem Druck, bei der das Volumen so ver ndert wird, dass der Druck konstant bleibt:

die Wärmekapazität ($C$) in Feststoffen und Fl ssigkeiten kann als eine Konstante $C$ betrachtet werden, die die nderung von ERROR:8085 und die Variación de Temperature ($\Delta T$) durch die Gleichung verkn pft:
| $ \Delta Q = C \Delta T $ |
Im Fall eines Gases h ngt der Zustand von die Absolute Temperatur ($T$), die Druck ($p$) und der Volumen ($V$) ab. Daher h ngt die Temperaturerh hung davon ab, ob das Volumen oder der Druck konstant gehalten wird, wenn W rme hinzugef gt wird. Im ersten Fall spricht man von die Wärmekapazität bei konstantem Druck ($C_p$) und bezeichnet es als $C_p$, und die Beziehung lautet wie folgt:
| $ \Delta Q = C_p \Delta T $ |
Wobei die Wärmekapazität bei konstantem Druck ($C_p$) durch der Spezifische Wärme bei konstantem Druck ($c_p$) und die Masse ($M$) gem folgender Beziehung ersetzt werden kann:
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
Daher erhalten wir:
| $ \Delta Q = c_p M \Delta T $ |
(ID 11189)
(ID 15303)
ID:(789, 0)
