Utilisateur:
Chaleur latente
Storyboard 
La chaleur latente est la quantité de chaleur nécessaire pour quun matériau change détat, cest-à-dire pour passer de létat solide à liquide, de liquide à gazeux ou directement de solide à gazeux. Elle est mesurée en réalisant le changement détat et en déterminant à la fois lénergie requise et la quantité de matière ayant subi cette transformation.
À léchelle microscopique, la chaleur latente correspond à lénergie nécessaire pour libérer une particule (atome ou molécule) dun cristal, lui permettant ainsi de rejoindre la phase liquide ou gazeuse. De manière similaire, dans le cas dun liquide, il sagit de la chaleur requise pour quune particule séchappe de sa surface et devienne une partie de la vapeur.
ID:(661, 0)
Chaleur latente
Image
Le principe de mesure de la chaleur latente consiste à effectuer un changement de phase et à mesurer l'énergie requise, comme illustré dans l'image suivante :
De cette manière, il est possible d'estimer l'énergie nécessaire pour vaporiser une masse donnée, ce qui correspond à la chaleur latente mesurée en J/kg ou en J/mol.
ID:(13543, 0)
Mesure de la chaleur d'évaporation
Image
La mesure de la chaleur de vaporisation s'effectue en chauffant un échantillon, provoquant ainsi son évaporation, tout en mesurant simultanément la chaleur fournie à l'échantillon. Ensuite, la vapeur est refroidie et condensée, et la masse originellement évaporée est mesurée.
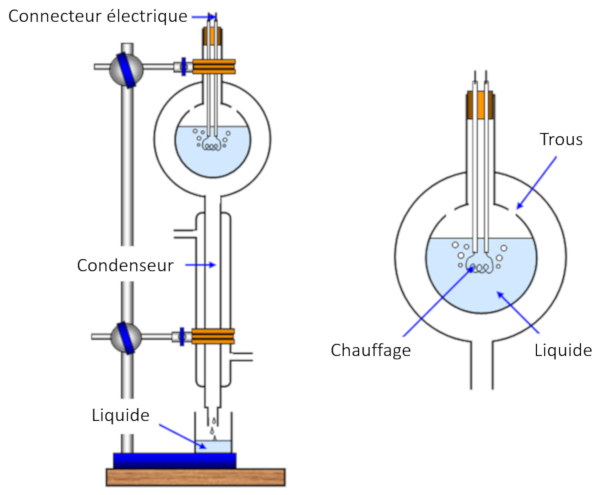
De cette manière, nous pouvons estimer l'énergie nécessaire pour vaporiser une masse donnée, ce qui correspond à chaleur latente ($L$) mesuré en joules par kilogramme (J/kg) ou joules par mole (J/mol).
ID:(1662, 0)
Mesure de la chaleur de fusion
Image
La mesure de la chaleur de vaporisation s'effectue en chauffant un échantillon, provoquant son évaporation tout en mesurant la chaleur fournie à l'échantillon. Ensuite, la vapeur est refroidie et condensée, et la masse qui a initialement évaporé est mesurée.
Ce processus permet d'estimer l'énergie nécessaire pour vaporiser une masse donnée, ce qui correspond à la chaleur latente mesurée en J/kg ou J/mol.
ID:(13541, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta Q = L \Delta m$
DQ = L * Dm
$ \Delta Q = T dS $
dQ = T * dS
$ l_m \equiv\displaystyle\frac{ L }{ M_m }$
l_m = L / M_m
$ m \equiv \displaystyle\frac{ \Delta m }{ N }$
m = M / N
$ m =\displaystyle\frac{ M_m }{ N_A }$
m = M_m / N_A
$ n = \displaystyle\frac{ \Delta m }{ M_m }$
n = M / M_m
$ n \equiv\displaystyle\frac{ N }{ N_A }$
n = N / N_A
ID:(15346, 0)
Chaleur latente spécifique
Équation
A masse évaporée ($\Delta m$) est défini en utilisant le chaleur latente ($L$) et le chaleur à changement de phase ($\Delta Q$) de la manière suivante :
| $ \Delta Q = L \Delta m$ |
ID:(3200, 0)
Deuxième loi de la thermodynamique
Équation
Le différence de chaleur inexacte ($\delta Q$) est égal à A température absolue ($T$) fois a variation d'entropie ($dS$) :
| $ \Delta Q = T dS $ |
| $ \delta Q = T dS $ |
ID:(9639, 0)
Masse des particules
Équation
Si nous divisons a masse ($M$) par le nombre de particules ($N$), nous obtenons a masse molaire ($m$) :
| $ m \equiv \displaystyle\frac{ \Delta m }{ N }$ |
| $ m \equiv \displaystyle\frac{ M }{ N }$ |
ID:(12829, 0)
Masse des particules et masse molaire
Équation
A masse molaire ($m$) peut être estimé à partir de a masse molaire ($M_m$) et le numéro d'Avogadro ($N_A$) en utilisant
| $ m =\displaystyle\frac{ M_m }{ N_A }$ |
ID:(4389, 0)
Concentration molaire
Équation
Le nombre de taupes ($n$) correspond à Le nombre de particules ($N$) divisé par le numéro d'Avogadro ($N_A$) :
| $ n \equiv\displaystyle\frac{ N }{ N_A }$ |
ID:(3748, 0)
Nombre de moles avec masse molaire
Équation
Le nombre de taupes ($n$) est déterminé en divisant a masse ($M$) d'une substance par son a masse molaire ($M_m$), ce qui correspond au poids d'une mole de la substance.
Par conséquent, la relation suivante peut être établie :
| $ n = \displaystyle\frac{ \Delta m }{ M_m }$ |
| $ n = \displaystyle\frac{ M }{ M_m }$ |
Le nombre de taupes ($n$) correspond à Le nombre de particules ($N$) divisé par le numéro d'Avogadro ($N_A$) :
Si nous multiplions à la fois le numérateur et le dénominateur par a masse molaire ($m$), nous obtenons :
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
Donc, c'est :
La masse molaire est exprimée en grammes par mole (g/mol).
ID:(4854, 0)