User:
Light and Colors
Storyboard 
One of the characteristics of the Light is its color. This is associated with the frequency of the wave and is proportional to the energy of the photon that represents light in its corpuscular description.
ID:(759, 0)
Photon energy
Equation
The color of light is associated with its the photon frequency ($\nu$), and there is a direct relationship between this frequency and the photon energy ($\epsilon$):
 $ \epsilon = h \nu $ |
where the planck constant ($h$) has a value of $6.62\times 10^{-34} , \text{Js}$.
ID:(3341, 0)
The spectre
Image
As the angle of refraction depends on the frequency or wavelength of light in glass, a prism can be used to decompose light into its different colors.
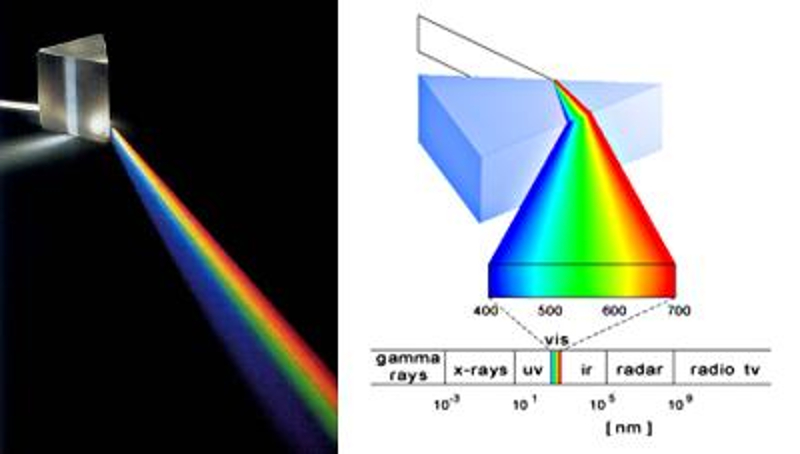
This results in what we call the spectrum of light.
ID:(6972, 0)
Refraction Index
Equation
The refractive index, denoted as $n$, is defined as the ratio of the speed of light in a vacuum, denoted as $c$, to the speed of light in the medium, denoted as $c_m$:
| $ n =\displaystyle\frac{ c }{ v }$ |
ID:(3192, 0)
Frequency and Wavelength of Photon
Equation
The photon is described as a wave, and the photon frequency ($\nu$) is related to ($$) through the speed of Light ($c$), according to the following formula:
| $ c = \nu \lambda $ |
Given that the photon frequency ($\nu$) is the inverse of the period ($T$):
$\nu=\displaystyle\frac{1}{T}$
this means that the speed of Light ($c$) is equal to the distance traveled in one oscillation, which is ($$), divided by the elapsed time, which corresponds to the period:
$c=\displaystyle\frac{\lambda}{T}$
In other words, the following relationship holds:
| $ c = \nu \lambda $ |
This formula corresponds to the mechanical relationship that states the wave speed is equal to the wavelength (distance traveled) divided by the oscillation period, or inversely proportional to the frequency (the inverse of the period).
ID:(3953, 0)
Refractive index and wavelength
Equation
If $n$ is the refractive index in a medium and $\lambda$ is the wavelength in a vacuum, then when propagating in the medium, the wavelength $\lambda_m$ will be
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
The energy of a wave or particle (photon) of light is given by
| $ \epsilon = h \nu $ |
When this energy propagates from one medium, for example, a vacuum with a speed of light $c$, to another medium with a speed of light $c_m$, it is concluded that the frequency of light remains unchanged. However, this implies that, since the speed of light is equal to the product of frequency and wavelength, as expressed in the equation
| $ c = \nu \lambda $ |
the wavelength must change as it transitions between mediums.
Therefore, if we have a wavelength of light in one medium $\lambda_m$ and in a vacuum $\lambda$, the refractive index can be defined as
| $ n =\displaystyle\frac{ c }{ v }$ |
and can be expressed as
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
In other words,
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
ID:(9776, 0)
The light and its colors
Image
A rainbow shows us that the light illuminating it is broken down into multiple colors. In fact, upon careful observation, you can see that there are multiple rainbows.
This is because each water droplet acts as a tiny circular prism, allowing for multiple refractions and the creation of multiple rainbows.
ID:(1625, 0)
Spectrum according to Newton
Image
Newton used a prism to decompose light into its components, believing he could identify a finite number of colors:
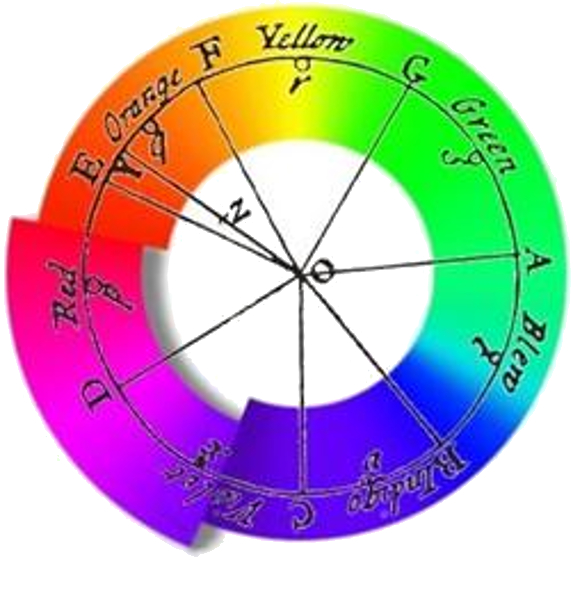
ID:(1682, 0)
Sir Isaac Newton
Image
The first to comprehend the structure of light as a physical entity was Sir Isaac Newton.
Sir Isaac Newton
(1643-1727)
Through a very simple experiment, he demonstrated that white light was composed of colors. However, he believed that the number of colors was discrete, as indicated in his chart representing his observations.
ID:(6971, 0)
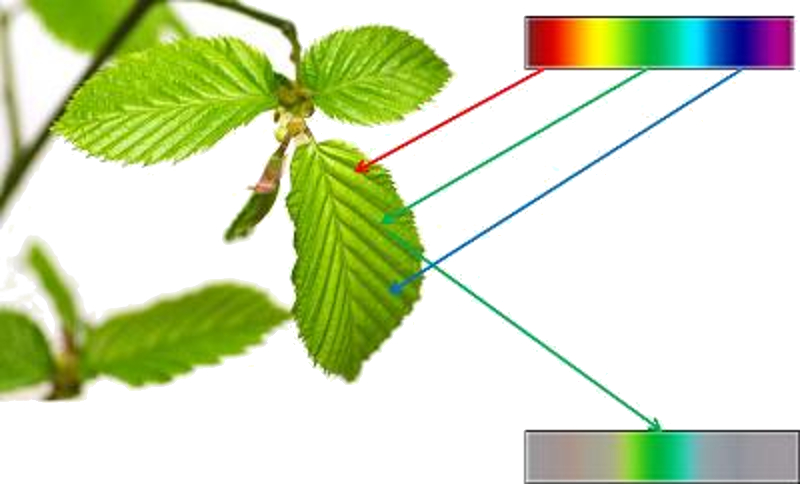
The reality of things
Image
The colors we see don't always necessarily correspond to reality. Our eyes capture light and generate electrical impulses based on the amount of blue, red, and green light we perceive. However, the intensity may not accurately represent the real proportions, leading to a perception that differs from reality:
ID:(12676, 0)
0
Video
Video: Light and Colors