Utilisateur:
Arc-en-ciel
Image 
Si vous observez un arc-en-ciel, vous verrez en réalité qu'il y a plusieurs arcs-en-ciel et que la séquence de couleurs se déplace : du bleu au rouge, puis du rouge au bleu, et ainsi de suite.
ID:(1844, 0)
Énergie photonique
Équation
La couleur de la lumière est associée à sa le fréquence des photons ($\nu$), et il existe une relation directe entre cette fréquence et a fréquence lumineuse ($\epsilon$) :
 $ \epsilon = h \nu $ |
où A constante de Planck ($h$) a une valeur de $6,62\times 10^{-34} , \text{Js}$.
ID:(3341, 0)
Le spectre
Image
Como l'angle de réfraction dépend de la fréquence ou de la longueur d'onde de la lumière dans le verre, on peut utiliser un prisme pour décomposer la lumière en ses différentes couleurs.
On obtient ce que l'on appelle le spectre de la lumière.
ID:(6972, 0)
Indice de réfraction
Équation
L'indice de réfraction, noté $n$, est défini comme le rapport de la vitesse de la lumière dans le vide, notée $c$, à la vitesse de la lumière dans le milieu, notée $c_m$:
| $ n =\displaystyle\frac{ c }{ v }$ |
ID:(3192, 0)
Fréquence et longueur d'onde des Photons
Équation
Le photon est décrit comme une onde, et le fréquence des photons ($\nu$) est liée à ($$) par a surface de la fontaine ($c$), selon la formule suivante :
| $ c = \nu \lambda $ |
Étant donné que le fréquence des photons ($\nu$) est l'inverse de le période ($T$) :
$\nu=\displaystyle\frac{1}{T}$
cela signifie que a surface de la fontaine ($c$) est égal à la distance parcourue en une oscillation, c'est-à-dire ($$), divisée par le temps écoulé, qui correspond à la période :
$c=\displaystyle\frac{\lambda}{T}$
En d'autres termes, la relation suivante s'applique :
| $ c = \nu \lambda $ |
Cette formule correspond à la relation mécanique qui établit que la vitesse de l'onde est égale à la longueur d'onde (distance parcourue) divisée par la période d'oscillation, ou inversement proportionnelle à la fréquence (l'inverse de la période).
ID:(3953, 0)
Indice de réfraction
Équation
Si $n$ est l'indice de réfraction dans un milieu et $\lambda$ est la longueur d'onde dans le vide, alors lors de la propagation dans le milieu, la longueur d'onde $\lambda_m$ sera
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
L'énergie d'une onde ou d'une particule (photon) de lumière est donnée par
| $ \epsilon = h \nu $ |
Lorsque cette énergie se propage d'un milieu, par exemple, un vide avec une vitesse de la lumière $c$, vers un autre milieu avec une vitesse de la lumière $c_m$, on en déduit que la fréquence de la lumière reste inchangée. Cependant, cela implique que, puisque la vitesse de la lumière est égale au produit de la fréquence et de la longueur d'onde, comme indiqué dans l'équation
| $ c = \nu \lambda $ |
la longueur d'onde doit changer lorsqu'elle passe d'un milieu à un autre.
Par conséquent, si nous avons une longueur d'onde de la lumière dans un milieu $\lambda_m$ et dans le vide $\lambda$, l'indice de réfraction peut être défini comme
| $ n =\displaystyle\frac{ c }{ v }$ |
et peut être exprimé comme
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
En d'autres termes,
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
ID:(9776, 0)
La lumière et ses couleurs
Image
Un arc-en-ciel nous montre que la lumière qui l'illumine se décompose en plusieurs couleurs. En fait, si on l'observe attentivement, on peut voir qu'il existe plusieurs arcs-en-ciel.
Cela s'explique par le fait que chaque goutte d'eau agit comme un petit prisme circulaire, ce qui permet de multiples réfractions et la création de plusieurs arcs-en-ciel.
ID:(1625, 0)
Spectre newtonien
Image
Newton a utilisé un prisme pour décomposer la lumière en ses composants, croyant qu'il pouvait identifier un nombre fini de couleurs :
ID:(1682, 0)
Sir Isaac Newton
Image
Le premier à comprendre la structure de la lumière en tant qu'entité physique fut Sir Isaac Newton.
Sir Isaac Newton
(1643-1727)
Grâce à une expérience très simple, il démontra que la lumière blanche était composée de couleurs. Cependant, il croyait que le nombre de couleurs était discret, comme le montre son graphique représentant ses observations.
ID:(6971, 0)
La réalité des choses
Image
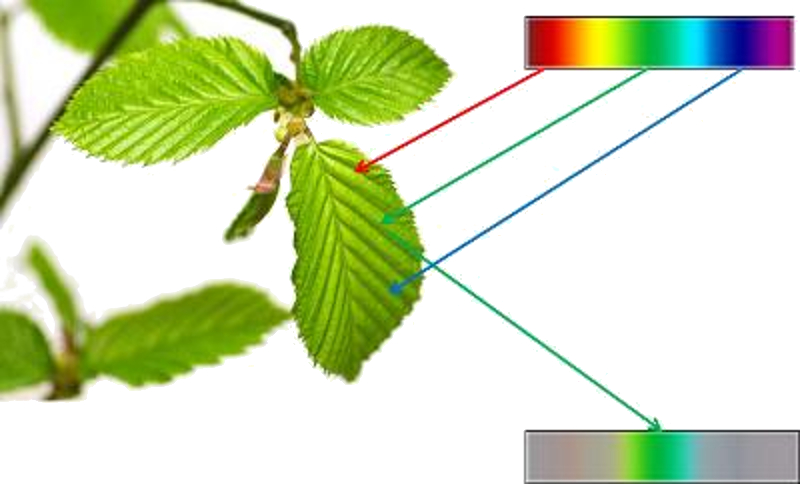
Les couleurs que nous voyons ne correspondent pas toujours nécessairement à la réalité. Nos yeux capturent la lumière et génèrent des impulsions électriques en fonction de la quantité de lumière bleue, rouge et verte que nous percevons. Cependant, l'intensité ne correspond pas toujours aux proportions réelles, ce qui entraîne une perception différente de la réalité :
ID:(12676, 0)
0
Video
Vidéo: Lumière et couleurs