Usuario:
Luz y Colores
Storyboard 
Una de las características de la Luz es su color. Este se asocia a la frecuencia de la onda y es proporcional a la energía que tiene el fotón que representa a la luz en su descripción corpuscular.
ID:(759, 0)
Energía del fotón
Ecuación
El color de la luz está asociado a su el frecuencia del fotón ($\nu$), y existe una relación directa entre esta frecuencia y la energía del fotón ($\epsilon$):
 $ \epsilon = h \nu $ |
donde la constante de Planck ($h$) tiene un valor de $6.62\times 10^{-34} , \text{Js}$.
ID:(3341, 0)
El espectro
Imagen
Como el ángulo de refracción depende de la frecuencia o longitud de onda de la luz en el vidrio, se puede usar un prisma para descomponer la luz en sus diferentes colores.
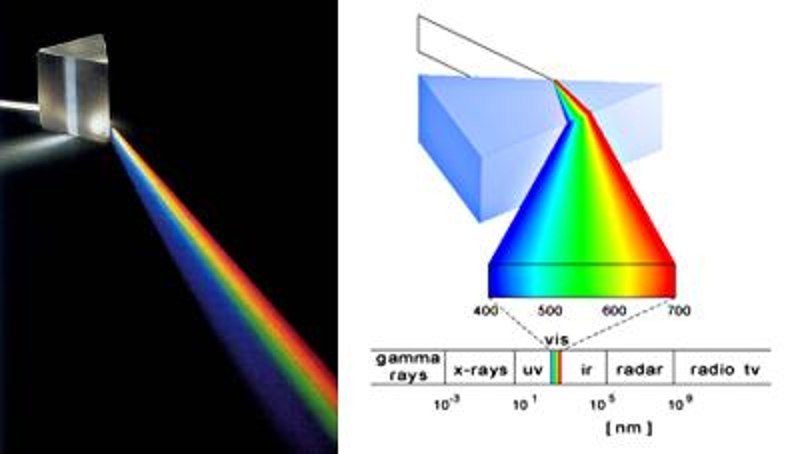
Espectro
Esto da lugar a lo que llamamos el espectro de luz.
ID:(6972, 0)
Indice de refracción
Ecuación
El índice de refracción, representado como $n$, se define como la razón entre la velocidad de la luz en el vacío, representada como $c$, y la velocidad de la luz en el medio, representada como $c_m$:
| $ n =\displaystyle\frac{ c }{ v }$ |
ID:(3192, 0)
Frecuencia y Largo de Onda de Fotónes
Ecuación
El fotón se describe como una onda, y el frecuencia del fotón ($\nu$) está relacionada con el largo de onda de luz visible ($\lambda$) a través de la velocidad de la luz ($c$), según la siguiente fórmula:
| $ c = \nu \lambda $ |
Dado que el frecuencia del fotón ($\nu$) es el inverso de el periodo ($T$):
$\nu=\displaystyle\frac{1}{T}$
esto significa que la velocidad de la luz ($c$) es igual a la distancia recorrida en una oscilación, es decir, el largo de onda de luz visible ($\lambda$), dividida por el tiempo transcurrido, que corresponde al período:
$c=\displaystyle\frac{\lambda}{T}$
En otras palabras, tenemos la siguiente relación:
| $ c = \nu \lambda $ |
Esta fórmula corresponde a la relación en mecánica que establece que la velocidad de la onda es igual a la longitud de onda (espacio recorrido) dividida por el periodo de oscilación, o inversamente proporcional a la frecuencia (el inverso del periodo).
ID:(3953, 0)
Indice de refracción y largo de onda
Ecuación
Si $n$ representa el índice de refracción en un medio y $\lambda$ es la longitud de onda en el vacío, entonces al propagarse en el medio, la longitud de onda $\lambda_m$ será
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
La energía de una onda o partícula de luz, representada por el fotón, está definida como
| $ \epsilon = h \nu $ |
Cuando esta energía se propaga de un medio, como el vacío, con una velocidad de la luz $c$, a otro medio con una velocidad de la luz $c_m$, se concluye que la frecuencia de la luz no cambia. Sin embargo, esto implica que, dado que la velocidad de la luz es igual al producto de la frecuencia y la longitud de onda, como se muestra en la ecuación
| $ c = \nu \lambda $ |
la longitud de onda debe ajustarse conforme cambia el medio.
Por lo tanto, si consideramos una longitud de onda de la luz en un medio $\lambda_m$ y en el vacío $\lambda$, podemos expresar el índice de refracción como
| $ n =\displaystyle\frac{ c }{ v }$ |
y se puede escribir de la siguiente manera:
$n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}$
En resumen,
| $ n =\displaystyle\frac{ \lambda }{ \lambda_m }$ |
ID:(9776, 0)
La luz y sus colores
Imagen
Un arco iris nos revela que la luz que lo ilumina se descompone en múltiples colores. De hecho, si se observa con atención, se puede apreciar la existencia de múltiples arco iris.
Esto ocurre porque cada gota de agua actúa como un pequeño prisma circular, lo que le permite realizar múltiples refracciones y generar así varios arco iris.
ID:(1625, 0)
Espectro según Newton
Imagen
Newton utilizó un prisma para descomponer la luz en sus componentes, creyendo que podía identificar un número finito de colores:
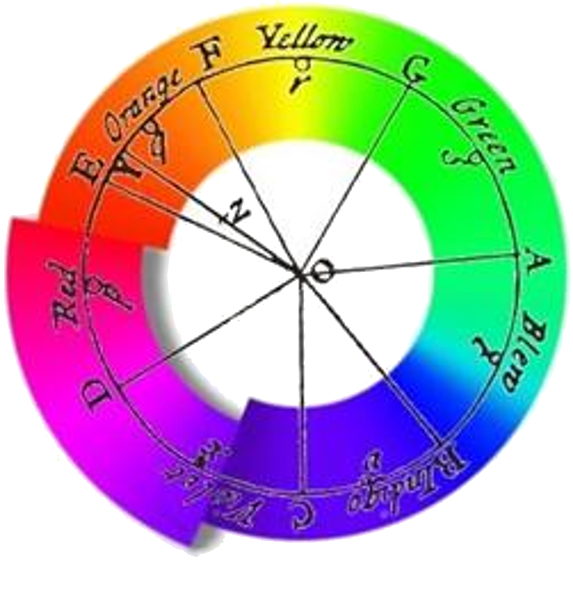
Dibujo de Newton coloreado con el espectro.
ID:(1682, 0)
Sir Isaac Newton
Imagen
El primero en comprender la naturaleza de la luz como una entidad física fue Sir Isaac Newton.
Sir Isaac Newton
(1643-1727)
Sir Isaac Newton
(1643-1727)
A través de un experimento muy sencillo, demostró que la luz blanca estaba compuesta por una variedad de colores. Sin embargo, creía que el número de colores era discreto, como lo indicaba en su gráfico que representaba sus observaciones.
ID:(6971, 0)
La realidad de las cosas
Imagen
Los colores que percibimos no siempre coinciden necesariamente con la realidad. Nuestros ojos captan la luz y generan impulsos eléctricos según la cantidad de luz azul, roja y verde que reciben. Sin embargo, la intensidad no siempre se corresponde con la proporción real, lo que hace que lo que percibimos sea diferente de la realidad:
Arco Iris múltiple
ID:(12676, 0)
0
Video
Video: Luz y Colores