Licht und Farben
Storyboard 
Eine der Eigenschaften des Lichts ist seine Farbe. Dies hängt mit der Frequenz der Welle zusammen und ist proportional zur Energie des Photons, das Licht in seiner Korpuskularbeschreibung darstellt.
ID:(759, 0)
Regenbogen
Bild 
Wenn Sie einen Regenbogen beobachten, werden Sie feststellen, dass es tatsächlich mehrere Regenbögen gibt und dass die Farbsequenz sich verschiebt: von Blau nach Rot und dann von Rot nach Blau und so weiter.
ID:(1844, 0)
Photon Energie
Gleichung 
Die Farbe des Lichts ist mit seiner der Photon Frequency (\nu) verbunden, und es gibt eine direkte Beziehung zwischen dieser Frequenz und die Photon energy (\epsilon):
wobei die Planck Konstante (h) einen Wert von 6,62\times 10^{-34} , \text{Js} hat.
ID:(3341, 0)
Das Spektrum
Bild 
Da der Brechungswinkel von der Frequenz oder Wellenlänge des Lichts im Glas abhängt, kann ein Prisma verwendet werden, um das Licht in seine verschiedenen Farben zu zerlegen.
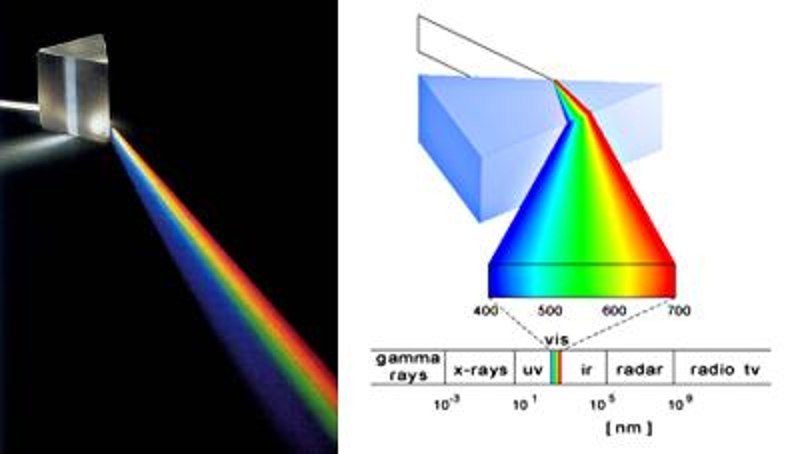
Dies führt zu dem, was wir als Lichtspektrum bezeichnen.
ID:(6972, 0)
Brechungsindex
Gleichung 
Der Brechungsindex, dargestellt als n, wird als das Verhältnis der Lichtgeschwindigkeit im Vakuum, dargestellt als c, zur Lichtgeschwindigkeit im Medium, dargestellt als c_m, definiert:
ID:(3192, 0)
Frequenz und Wellenlänge von Photon
Gleichung 
Das Photon wird als Welle beschrieben, und der Photon Frequency (\nu) steht in Beziehung zu ($$) durch die Lichtgeschwindigkeit (c), gemäß der folgenden Formel:
Da die Frequenz das Reziprokum der Zeit für eine Schwingung ist:
\nu=\displaystyle\frac{1}{T}
bedeutet dies, dass die Lichtgeschwindigkeit gleich der Strecke ist, die in einer Schwingung zurückgelegt wird, das ist die Wellenlänge, geteilt durch die benötigte Zeit, das ist die Periode:
c=\displaystyle\frac{\lambda}{T}
Mit anderen Worten:
| c = \nu \lambda |
Diese Formel entspricht der mechanischen Beziehung, die besagt, dass die Wellengeschwindigkeit gleich der Wellenlänge (zurückgelegte Strecke) geteilt durch die Schwingungsperiode ist, oder umgekehrt proportional zur Frequenz (dem Kehrwert der Periode).
ID:(3953, 0)
Brechungsindex und Wellenlänge
Gleichung 
Wenn n der Brechungsindex in einem Medium ist und \lambda die Wellenlänge im Vakuum ist, wird die Wellenlänge \lambda_m beim Propagieren im Medium sein
Die Energie einer Welle oder eines Teilchens (Photon) des Lichts wird durch
| \epsilon = h \nu |
ausgedrückt. Wenn diese Energie von einem Medium, zum Beispiel einem Vakuum mit der Lichtgeschwindigkeit c, in ein anderes Medium mit der Lichtgeschwindigkeit c_m übergeht, folgt daraus, dass die Frequenz des Lichts unverändert bleibt. Allerdings bedeutet dies, dass sich die Wellenlänge ändern muss, da die Lichtgeschwindigkeit gleich dem Produkt aus Frequenz und Wellenlänge ist, wie in der Gleichung
| c = \nu \lambda |
ausgedrückt wird.
Daher kann, wenn wir eine Wellenlänge des Lichts in einem Medium \lambda_m und im Vakuum \lambda betrachten, der Brechungsindex definiert werden als
| n =\displaystyle\frac{ c }{ v } |
und kann wie folgt ausgedrückt werden:
n=\displaystyle\frac{c}{c_m}=\displaystyle\frac{\lambda\nu}{\lambda_m\nu}=\displaystyle\frac{\lambda}{\lambda_m}
Mit anderen Worten,
| n =\displaystyle\frac{ \lambda }{ \lambda_m } |
ID:(9776, 0)
Das Licht und seine Farben
Bild 
Ein Regenbogen zeigt uns, dass das Licht, das ihn erhellt, in mehrere Farben zerlegt wird. Tatsächlich kann man bei genauer Beobachtung erkennen, dass es mehrere Regenbogen gibt.
Dies liegt daran, dass jede Wassertropfen als ein kleines kreisförmiges Prisma fungiert, was mehrere Brechungen ermöglicht und so mehrere Regenbogen erzeugt.
ID:(1625, 0)
Spektrum nach Newton
Bild 
Newton verwendete ein Prisma, um Licht in seine Bestandteile zu zerlegen, in der Überzeugung, dass er eine begrenzte Anzahl von Farben identifizieren konnte:
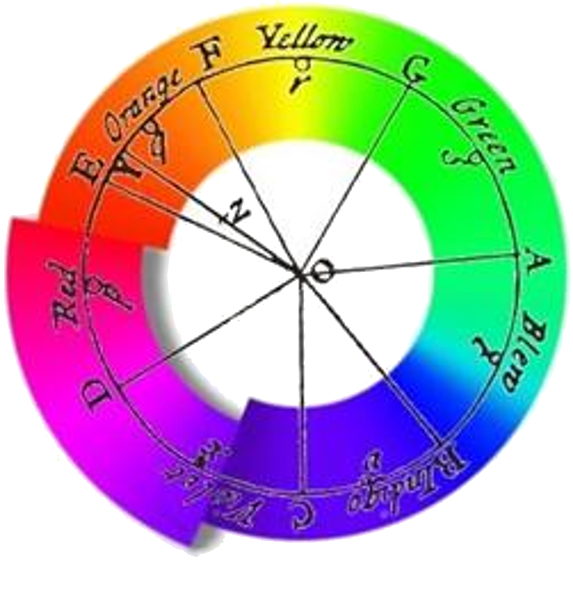
ID:(1682, 0)
Sir Isaac Newton
Bild 
Der erste, der die Struktur des Lichts als eine physikalische Erscheinung verstand, war Sir Isaac Newton.

Sir Isaac Newton
(1643-1727)
Mit einem sehr einfachen Experiment zeigte er, dass weißes Licht aus verschiedenen Farben zusammengesetzt ist. Er glaubte jedoch, dass die Anzahl der Farben diskret war, wie in seiner Grafik dargestellt, die seine Beobachtungen verdeutlicht.
ID:(6971, 0)
Die Realität der Dinge
Bild 
Die Farben, die wir sehen, entsprechen nicht immer zwangsläufig der Realität. Unsere Augen erfassen Licht und erzeugen elektrische Impulse basierend auf der Menge an blauem, rotem und grünem Licht, das wir wahrnehmen. Allerdings entspricht die Intensität nicht immer den realen Proportionen, was dazu führt, dass unsere Wahrnehmung von der Realität abweichen kann:

ID:(12676, 0)
0
Video
Video: Licht und Farben
