Forcer de Stokes
Storyboard 
Un exemple de force visqueuse est le modèle qui se produit lorsqu'une sphère se déplace dans un milieu visqueux. Ce modèle et l'équation associée sont connus sous le nom de leur auteur, George Stokes.
La force de Stokes dépend de la viscosité du milieu, du rayon de la sphère et de la vitesse à laquelle elle se déplace dans le milieu. De manière similaire, si le milieu lui-même est en mouvement, il entraîne l'objet avec lui.
ID:(1964, 0)
Forcer de Stokes
Storyboard 
Un exemple de force visqueuse est le modèle qui se produit lorsqu'une sphère se déplace dans un milieu visqueux. Ce modèle et l'équation associée sont connus sous le nom de leur auteur, George Stokes. La force de Stokes dépend de la viscosité du milieu, du rayon de la sphère et de la vitesse à laquelle elle se déplace dans le milieu. De manière similaire, si le milieu lui-même est en mouvement, il entraîne l'objet avec lui.
Variables
Calculs
Calculs
Équations
tant donn que le moment ($p$) est d fini avec a masse d'inertie ($m_i$) et a vitesse ($v$),
Si a masse d'inertie ($m_i$) est gal a masse initiale ($m_0$), alors nous pouvons d river la quantit de mouvement par rapport au temps et obtenir a force à masse constante ($F$) :
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Par cons quent, nous en concluons que
Si le temps caract ristique est d fini comme
$\tau=\displaystyle\frac{m_i}{b}$
et que le coefficient de la force visqueuse est
$b=6\pi r\eta$
D'autre part, en consid rant que
et
on en d duit que la masse est
$m_i = \rho V = \displaystyle\frac{4\pi}{3} r^3 \rho$
ce qui conduit
$\tau = \displaystyle\frac{m_i}{b}=\displaystyle\frac{2 \rho r^2}{9\eta}$
en d'autres termes,
Exemples
George Stokes a r alis d\'importantes avanc es dans les domaines de l\'hydrodynamique et des math matiques. Il est principalement connu pour la c l bre loi de Stokes appliqu e aux corps sph riques dans un coulement et pour le th or me de Stokes en math matiques.
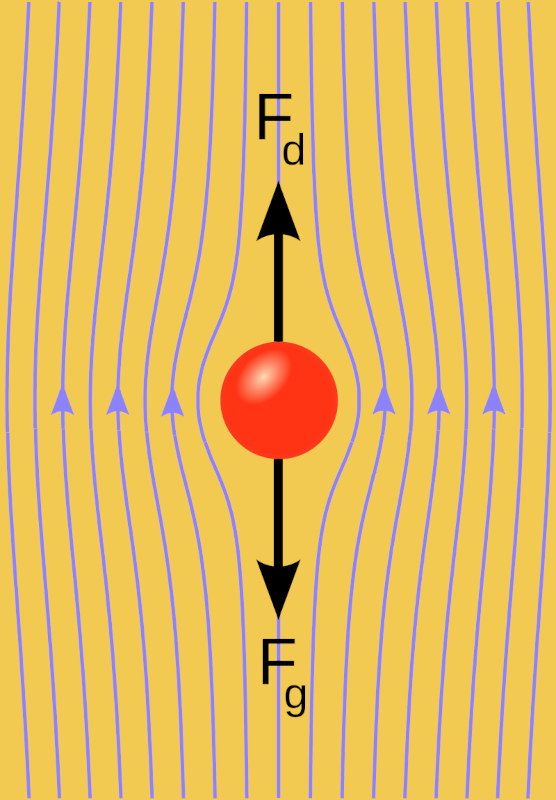
Lorsqu'une sph re est jet e dans un milieu visqueux, une force initiale ascendante, une force gravitationnelle ($F_g$), appara t, entra nant progressivement l'enfoncement du corps. Pendant ce processus, la sph re gagne en vitesse, ce qui entra ne une force descendante, une force visqueuse ($F_v$), d pendante de la vitesse. Au fur et mesure que la vitesse totale, a force à masse constante ($F$),
commence diminuer jusqu' devenir nulle. partir de ce moment, le mouvement continue une vitesse constante, car il n'y a pas de force pour l'acc l rer.
La force de Stokes est la force g n r e par l' coulement autour d'une sph re de ERROR:6690,0 immerg e dedans. Dans ce cas, on utilise le mod le de force proportionnelle a vitesse ($v$) :
Dans ce contexte, on peut d montrer que a constante de force visqueuse ($b$) avec a viscosité ($\eta$) est gal :
par cons quent, la force de Stokes s'exprime comme suit :
Cette force s'applique principalement dans les coulements laminaires.
Le mouvement d'une sph re en deux dimensions est caract ris par a composante x de la vitesse ($v_x$) avec a vitesse horizontale initiale ($v_{0x}$), a temps d'adaptation ($\tau$) et le temps ($t$) :
et a composante y de la vitesse ($v_y$) avec a vitesse verticale initiale ($v_{0y}$), a temps d'adaptation ($\tau$), a accélération gravitationnelle ($g$) et le temps ($t$) :
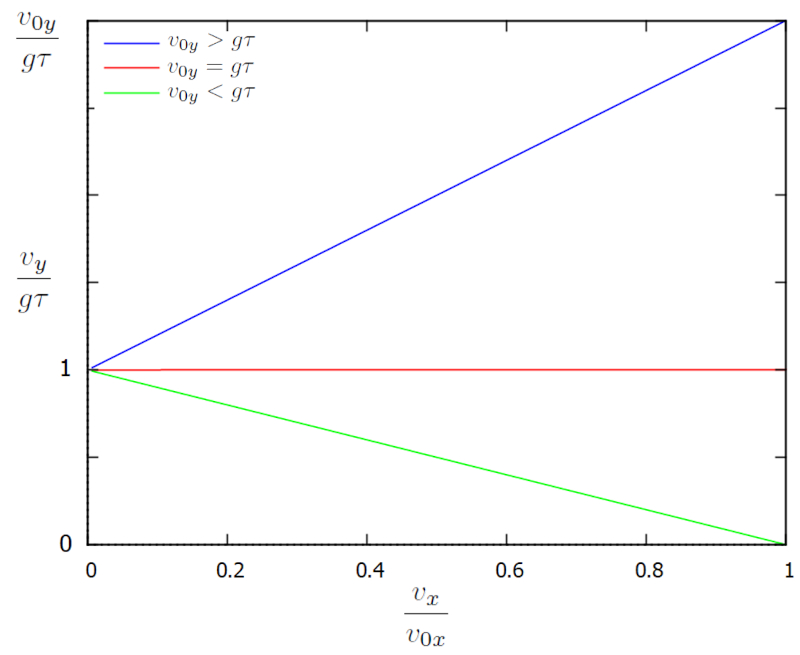
ce qui est repr sent dans un diagramme $v_x$ vs $v_y$ :
Le diagramme montre comment les deux composantes de la vitesse voluent dans le temps. Initialement, $v$ est gal $v_{0x}$, ce qui correspond un point sur le bord droit du graphique. Au fil du temps, les composantes de la vitesse voluent de la droite vers le bord gauche, o la vitesse horizontale est nulle et la vitesse verticale atteint la limite de $g\tau$, de sorte que $v/g\tau$ est gal un.
La d placement horizontal peut tre calcul en utilisant l' quation pour a position sur l'axe des x ($x$) avec a position initiale sur l'axe des x ($x_0$), a vitesse horizontale initiale ($v_{0x}$), a temps d'adaptation ($\tau$) et le temps ($t$) :
et le d placement vertical pour a position sur l'axe y ($y$) avec a position initiale sur l'axe y ($y_0$), a vitesse horizontale initiale ($v_{0x}$), a temps d'adaptation ($\tau$) et le temps ($t$) :
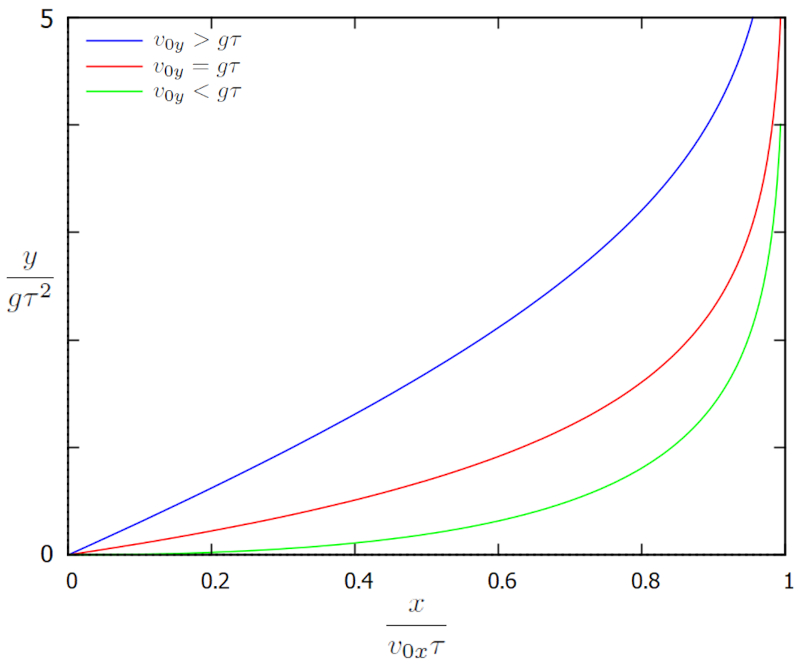
ce qui est graphiquement repr sent dans les positions $x$ vs $y$ :
Dans ce cas, la position volue du bord gauche vers la droite, o pour le mouvement horizontal atteignant une distance maximale de $v_{0x}\tau$. Le d placement vertical est d crit avec un syst me de coordonn es ayant son origine au point o la trajectoire commence et dont la version verticale pointe vers le bas. Dans ce sens, l'augmentation de $y$ correspond au mouvement descendant de la sph re dans la direction de la gravit .
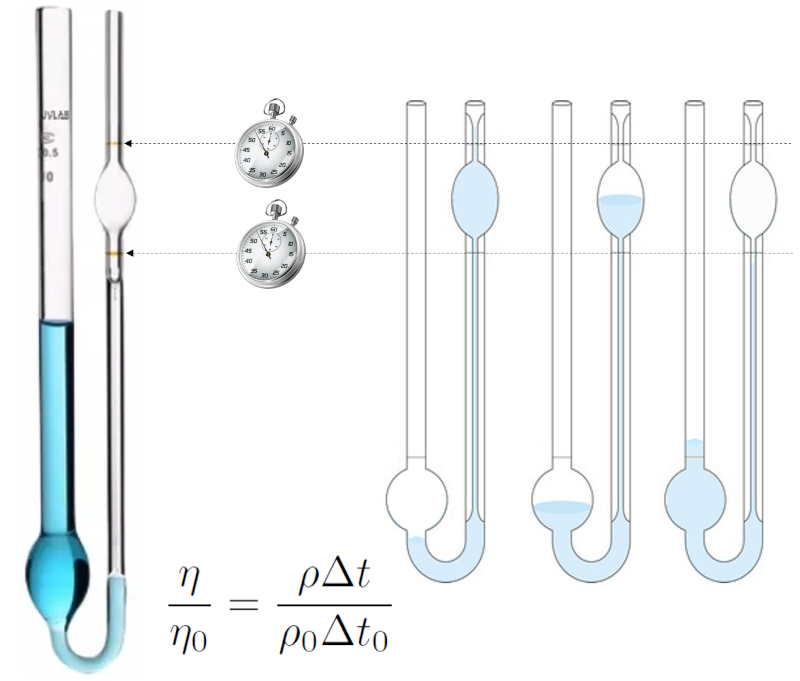
La m thode de mesure de la viscosit d'Ostwald est bas e sur le comportement d'un liquide s' coulant travers un tube de petit rayon (capillaire).
Le liquide est introduit, une aspiration est appliqu e pour d passer la marque sup rieure, puis il est laiss s' couler, mesurant le temps qu'il faut pour que le niveau passe de la marque sup rieure la marque inf rieure.
L'exp rience est d'abord r alis e avec un liquide pour lequel la viscosit et la densit sont connues (par exemple, de l'eau distill e), puis avec le liquide pour lequel la viscosit doit tre d termin e. Si les conditions sont identiques, le liquide qui s' coule dans les deux cas sera similaire, et ainsi, le temps sera proportionnel la densit divis e par la viscosit . Ainsi, une quation de comparaison entre les deux viscosit s peut tre tablie :
Dans le cas d'un corps tombant dans un milieu visqueux, la force totale, a force à masse constante ($F$), est gale a force gravitationnelle ($F_g$) moins a force visqueuse ($F_v$), donc
Dans le cas o a masse d'inertie ($m_i$) est gal a masse initiale ($m_0$),
la d riv e de la quantit de mouvement sera gale la masse multipli e par la d riv e de a vitesse ($v$). Comme la d riv e de la vitesse est a accélération instantanée ($a$), nous avons que a force à masse constante ($F$) est gal
A force gravitationnelle ($F_g$) est bas sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui refl te l'intensit de la gravit la surface de la plan te. Cette derni re est identifi e par a accélération gravitationnelle ($g$), qui est gal $9.8 m/s^2$.
Par cons quent, on en conclut que :
La forme la plus simple de a force visqueuse ($F_v$) est celle qui est proportionnelle au a vitesse ($v$) du corps, repr sent e par :
La constante de proportionnalit , galement connue sous le nom de a constante de force visqueuse ($b$), d pend g n ralement de la forme de l'objet et de la viscosit du milieu travers lequel il se d place. Un exemple de ce type de force est celle exerc e par un flux de fluide sur un corps sph rique, dont l'expression math matique est connue sous le nom de loi de Stokes.
La force de Stokes est la force g n r e par l' coulement autour d'une sph re immerg e en son sein. Dans ce cas, le mod le de la force proportionnelle la vitesse est utilis :
La force de tra n e est d finie en fonction de la viscosit du fluide et de la vitesse de la sph re selon l' quation :
Stokes a explicitement calcul la r sistance subie par la sph re et a d termin que la viscosit est proportionnelle au rayon de la sph re et sa vitesse, ce qui nous donne la relation suivante :
Dans le cas de la force de Stokes sur a force visqueuse ($F_v$), elle est mod lis e avec a constante de force visqueuse ($b$) et a vitesse ($v$),
ce qui correspond une valeur de a constante de force visqueuse ($b$) qui, avec a viscosité ($\eta$) et ERROR:6690, est gale
A force à masse constante ($F$) est gal a force gravitationnelle ($F_g$) moins a force visqueuse ($F_v$), donc :
Cette relation permet d' tablir l' quation de mouvement pour a accélération instantanée ($a$) avec une masse d'inertie ($m_i$) qui chute en raison de la gravit terrestre avec a accélération gravitationnelle ($g$), et avec une masse gravitationnelle ($m_g$), en a constante de force visqueuse ($b$), prendra la forme de :
A volume d'une sphère ($V$) pour une sph re avec un rayon d'une sphère ($r$) est calcul e selon la formule suivante :
Les masses que Newton a utilis es dans ses principes sont li es l'inertie des corps, ce qui conduit au concept de a masse d'inertie ($m_i$).
La loi de Newton, qui est li e la force entre les corps en raison de leurs masses, est associ e la gravit et est donc connue sous le nom de a masse gravitationnelle ($m_g$).
Empiriquement, on a conclu que les deux masses sont quivalentes, et donc nous d finissons
Einstein a t celui qui a remis en question cette galit et, partir de ce doute, a compris pourquoi les deux 'apparaissent' gales dans sa th orie de la gravit . Dans son argument, Einstein a expliqu que les masses d forment l'espace, et cette d formation de l'espace provoque un changement dans le comportement des corps. Ainsi, les masses s'av rent tre quivalentes. Le concept r volutionnaire de la courbure de l'espace implique m me que la lumi re, qui n'a pas de masse, est affect e par les corps c lestes, ce qui contredit la th orie de la gravitation de Newton. Cela a t d montr exp rimentalement en tudiant le comportement de la lumi re lors d'une clipse solaire. Dans cette situation, les faisceaux lumineux sont d vi s en raison de la pr sence du soleil, permettant l'observation des toiles qui se trouvent derri re lui.
Avec le mod le de Stokes, la force visqueuse a constante de force visqueuse ($b$), qui d pend de ERROR:6690 et de a viscosité de l'environnement ($\eta$), calcul e avec
conduit ce que a temps de viscosité et masse d'inertie ($\tau_i$) et a temps de viscosité et masse gravitationnelle ($\tau_g$) prennent des valeurs gales a temps d'adaptation ($\tau$), calcul es avec a densité ($\rho$) par l'interm diaire de
Dans le sc nario de mouvement horizontal, la sph re rencontre une r sistance uniquement due la viscosit du milieu environnant, qui peut tre quantifi e par l' quation impliquant a vitesse ($v$) avec a vitesse initiale ($v_0$), a temps de viscosité et masse d'inertie ($\tau_i$) et le temps ($t$) :
En cons quence, l'interaction entre ces l ments conduit l'observation que a composante x de la vitesse ($v_x$) avec a vitesse horizontale initiale ($v_{0x}$), a temps d'adaptation ($\tau$) et le temps ($t$) :
Dans le contexte du mouvement horizontal, la position est obtenue en int grant la vitesse, ce qui nous donne une quation en a position ($s$) avec a vitesse ($s_0$), a vitesse initiale ($v_0$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a temps de viscosité et masse d'inertie ($\tau_i$), a accélération gravitationnelle ($g$) et le temps ($t$) :
A partir de cette quation, nous arrivons l' quation de d placement horizontal pour a position sur l'axe des x ($x$) avec a position initiale sur l'axe des x ($x_0$), a vitesse horizontale initiale ($v_{0x}$), a temps d'adaptation ($\tau$) et le temps ($t$) :
Avec l' quation de mouvement d'un corps dans un milieu visqueux, nous avons la d riv e de a vitesse ($v$) Le temps ($t$) avec a constante de force visqueuse ($b$) et a accélération gravitationnelle ($g$) :
Cela d finit a temps de viscosité et masse d'inertie ($\tau_i$) comme :
Dans le contexte du mouvement vertical, la sph re est confront e une double r sistance : d'une part, la viscosit du milieu environnant, et d'autre part, la gravit qui la pousse vers le bas. Cette derni re peut tre quantifi e par l' quation en a vitesse ($v$) avec a vitesse initiale ($v_0$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a temps de viscosité et masse d'inertie ($\tau_i$), a accélération gravitationnelle ($g$) et le temps ($t$) :
Nous supposons que la masse gravitationnelle et la masse inertielle sont identiques, alors nous obtenons la fonction pour a composante y de la vitesse ($v_y$) avec a vitesse verticale initiale ($v_{0y}$), a temps d'adaptation ($\tau$), a accélération gravitationnelle ($g$) et le temps ($t$) :
Dans le contexte du mouvement vertical, la position est obtenue en int grant la vitesse, ce qui nous donne une quation en a position ($s$) avec a vitesse ($s_0$), a vitesse initiale ($v_0$), a temps de viscosité et masse gravitationnelle ($\tau_g$), a temps de viscosité et masse d'inertie ($\tau_i$), a accélération gravitationnelle ($g$) et le temps ($t$) :
partir de cette quation, nous arrivons l' quation de d placement vertical pour a position sur l'axe y ($y$) avec a position initiale sur l'axe y ($y_0$), a vitesse horizontale initiale ($v_{0x}$), a temps d'adaptation ($\tau$) et le temps ($t$) :
ID:(1964, 0)