Stokes Kraft
Storyboard 
Ein Beispiel für eine viskose Kraft ist das Modell, das entsteht, wenn sich eine Kugel in einem viskosen Medium bewegt. Dieses Modell und die zugehörige Gleichung sind bekannt unter dem Namen ihres Autors George Stokes.
Die Stokes'sche Kraft hängt von der Viskosität des Mediums, dem Radius der Kugel und der Geschwindigkeit ab, mit der sie sich im Medium bewegt. Ebenso zieht, wenn sich das Medium selbst bewegt, dieses das Objekt mit sich.
ID:(1964, 0)
Stokes Kraft
Storyboard 
Ein Beispiel für eine viskose Kraft ist das Modell, das entsteht, wenn sich eine Kugel in einem viskosen Medium bewegt. Dieses Modell und die zugehörige Gleichung sind bekannt unter dem Namen ihres Autors George Stokes. Die Stokes'sche Kraft hängt von der Viskosität des Mediums, dem Radius der Kugel und der Geschwindigkeit ab, mit der sie sich im Medium bewegt. Ebenso zieht, wenn sich das Medium selbst bewegt, dieses das Objekt mit sich.
Variablen
Berechnungen
Berechnungen
Gleichungen
Da der Moment ($p$) mit die Träge Masse ($m_i$) und die Geschwindigkeit ($v$) definiert ist,
Wenn die Träge Masse ($m_i$) gleich die Anfangsmasse ($m_0$) ist, k nnen wir den Impuls nach der Zeit ableiten und die Kraft mit konstanter Masse ($F$) erhalten:
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Daher kommen wir zu dem Schluss, dass
Wenn die charakteristische Zeit definiert ist als
$\tau=\displaystyle\frac{m_i}{b}$
und der Koeffizient der viskosen Kraft ist
$b=6\pi r\eta$
Auf der anderen Seite, unter Ber cksichtigung von
und
folgt, dass die Masse ist
$m_i = \rho V = \displaystyle\frac{4\pi}{3} r^3 \rho$
was zu
$\tau = \displaystyle\frac{m_i}{b}=\displaystyle\frac{2 \rho r^2}{9\eta}$
f hrt, mit anderen Worten,
Beispiele
George Stokes leistete bedeutende Beitr ge auf den Gebieten der Hydrodynamik und Mathematik. Er wird vor allem f r das bekannte Stokes-Gesetz f r kugelf rmige K rper in einem Str mungsfeld und f r den Stokes\'schen Satz in der Mathematik in Erinnerung behalten.
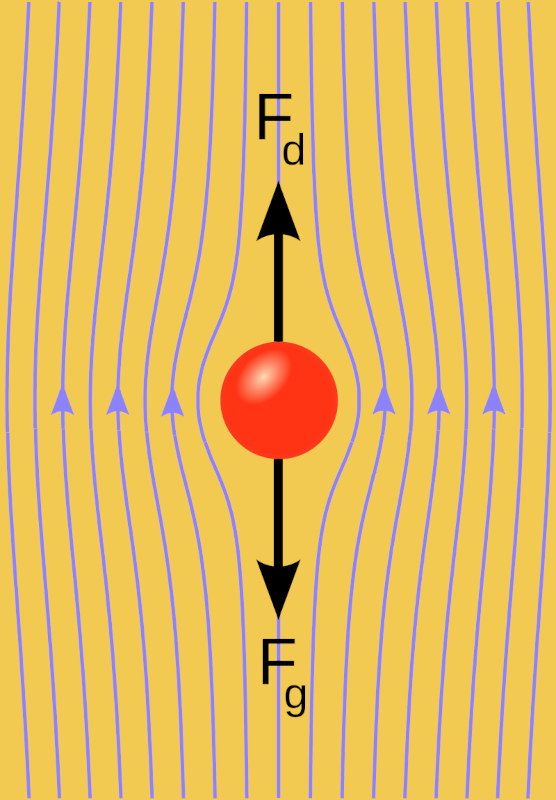
Wenn eine Kugel in ein viskoses Medium geworfen wird, entsteht eine anf ngliche Aufw rtskraft, eine Schwerkraft ($F_g$), die den K rper allm hlich absinken l sst. W hrend dieses Prozesses gewinnt die Kugel an Geschwindigkeit, was zu einer abw rts gerichteten Kraft, eine Viscose Kraft ($F_v$), f hrt, die von der Geschwindigkeit abh ngt. Wenn die Gesamtgeschwindigkeit, die Kraft mit konstanter Masse ($F$),
beginnt sich zu verringern, bis sie null ist. Ab diesem Moment setzt sich die Bewegung mit konstanter Geschwindigkeit fort, da keine Kraft vorhanden ist, die sie beschleunigt.
Die Stokes-Kraft ist die Kraft, die durch den Fluss um eine in ihn eingetauchte Kugel von ERROR:6690,0 erzeugt wird. In diesem Fall wird das Modell der Kraft verwendet, die proportional zu die Geschwindigkeit ($v$) ist:
In diesem Kontext kann gezeigt werden, dass die Konstante des Viscose Kraft ($b$) mit die Viskosität ($\eta$) gleich ist:
somit wird die Stokes-Kraft wie folgt ausgedr ckt:
Diese Kraft wird haupts chlich in laminaren Str mungen angewendet.
Die Bewegung einer Kugel in zwei Dimensionen wird durch die Komponente x der Geschwindigkeit ($v_x$) mit die Horizontale Geschwindigkeit ($v_{0x}$), die Anpassungszeit ($\tau$) und der Zeit ($t$) charakterisiert:
und die Komponente y der Geschwindigkeit ($v_y$) mit die Vertikale Geschwindigkeit ($v_{0y}$), die Anpassungszeit ($\tau$), die Gravitationsbeschleunigung ($g$) und der Zeit ($t$):
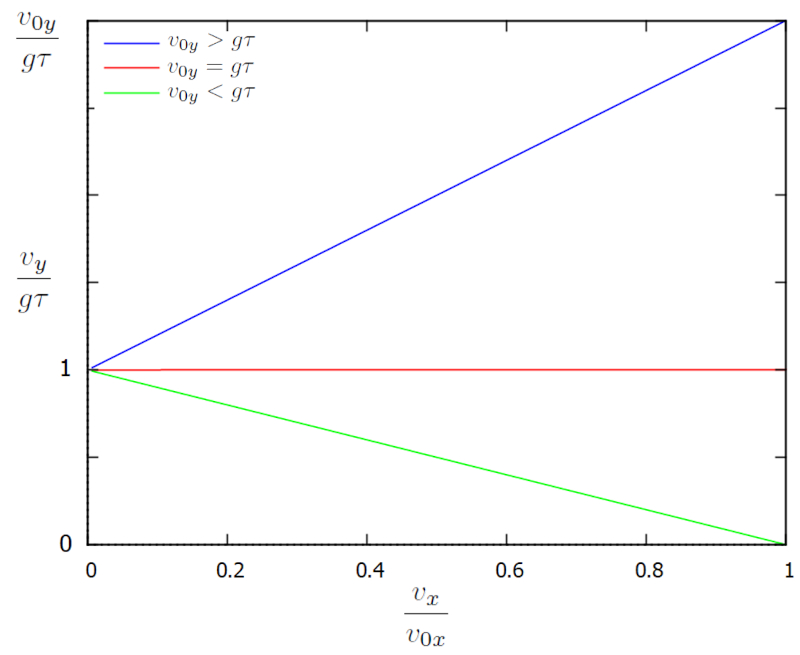
was in einem $v_x$ vs. $v_y$ Diagramm dargestellt wird:
Das Diagramm zeigt, wie sich beide Geschwindigkeitskomponenten im Laufe der Zeit entwickeln. Anfangs entspricht $v$ $v_{0x}$, was einem Punkt am rechten Rand des Graphen entspricht. Im Laufe der Zeit entwickeln sich die Geschwindigkeitskomponenten von der rechten Seite zum linken Rand, wo die horizontale Geschwindigkeit null ist und die vertikale Geschwindigkeit das Limit $g\tau$ erreicht, sodass $v/g\tau$ eins entspricht.
Die horizontale Verschiebung kann mithilfe der Gleichung f r die Position auf der x-Achse ($x$) mit die Ausgangsposition auf der x-Achse ($x_0$), die Horizontale Geschwindigkeit ($v_{0x}$), die Anpassungszeit ($\tau$) und der Zeit ($t$) berechnet werden:
und die vertikale Verschiebung f r die Position auf der y-Achse ($y$) mit die Ausgangsposition auf der y-Achse ($y_0$), die Horizontale Geschwindigkeit ($v_{0x}$), die Anpassungszeit ($\tau$) und der Zeit ($t$):
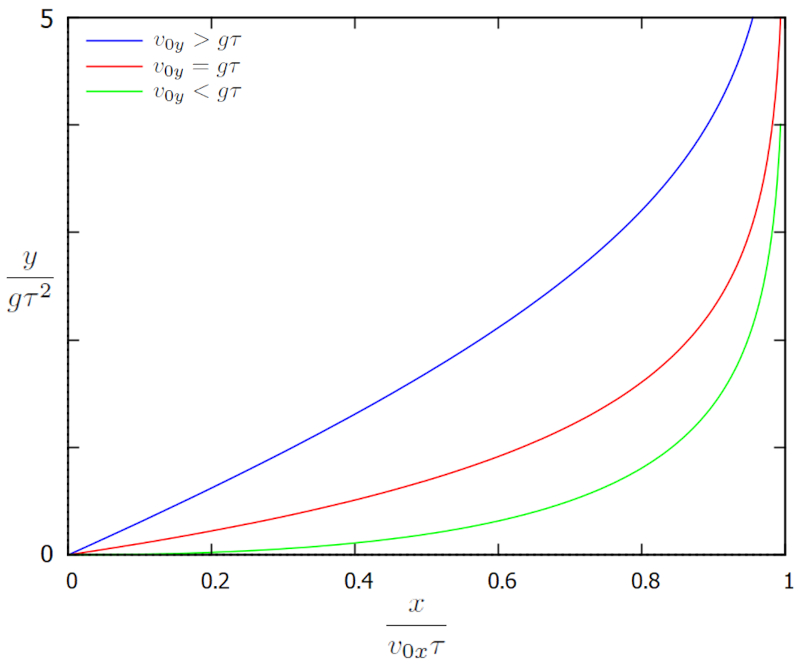
die in den Positionen $x$ vs $y$ graphisch dargestellt wird:
In diesem Fall entwickelt sich die Position von der linken Kante zur rechten, wo sie in ihrer horizontalen Bewegung stoppt und einen maximalen Abstand von $v_{0x}\tau$ erreicht. Die vertikale Verschiebung wird mit einem Koordinatensystem beschrieben, dessen Ursprung der Punkt ist, an dem die Trajektorie beginnt, und dessen vertikale Version nach unten zeigt. In diesem Sinne entspricht die Zunahme von $y$ dem Abstieg der Kugel in Richtung der Schwerkraft.
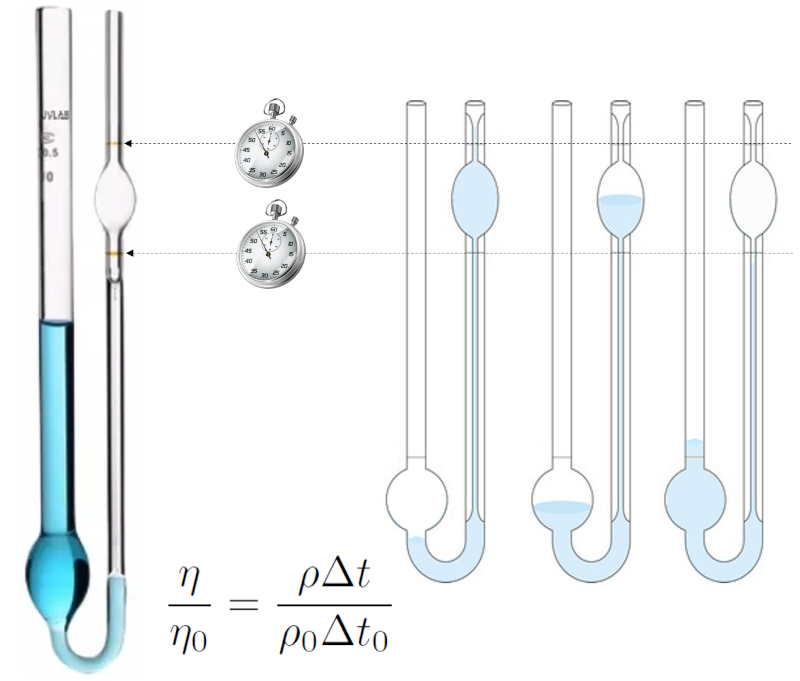
Die Viskosit tsmessmethode nach Ostwald basiert auf dem Verhalten eines Fl ssigkeitsstroms durch ein Rohr mit kleinem Radius (Kapillare).
Die Fl ssigkeit wird eingef hrt, Unterdruck wird angewendet, um die obere Markierung zu berschreiten, und dann wird sie abflie en gelassen, wobei die Zeit gemessen wird, die der Pegel ben tigt, um von der oberen zur unteren Markierung zu gelangen.
Das Experiment wird zuerst mit einer Fl ssigkeit durchgef hrt, deren Viskosit t und Dichte bekannt sind (z. B. destilliertes Wasser), und dann mit der Fl ssigkeit, f r die die Viskosit t bestimmt werden soll. Wenn die Bedingungen identisch sind, wird die in beiden F llen flie ende Fl ssigkeit hnlich sein, und somit wird die Zeit proportional zur Dichte durch die Viskosit t sein. Somit kann eine Vergleichsgleichung zwischen beiden Viskosit ten aufgestellt werden:
Im Fall eines K rpers, der in einem viskosen Medium f llt, ist die Gesamtkraft, die Kraft mit konstanter Masse ($F$), gleich die Schwerkraft ($F_g$) minus die Viscose Kraft ($F_v$), also
Im Fall, dass die Träge Masse ($m_i$) gleich die Anfangsmasse ($m_0$) ist,
wird die Ableitung des Impulses gleich der Masse mal der Ableitung von die Geschwindigkeit ($v$) sein. Da die Ableitung der Geschwindigkeit die Augenblickliche Beschleunigung ($a$) ist, ergibt sich, dass die Kraft mit konstanter Masse ($F$) ist
Die Schwerkraft ($F_g$) basiert auf die Gravitationsmasse ($m_g$) des Objekts und auf einer Konstanten, die die Intensit t der Gravitation an der Oberfl che des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$) identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
Die einfachste Form von die Viscose Kraft ($F_v$) ist diejenige, die proportional zum die Geschwindigkeit ($v$) des K rpers ist, dargestellt durch:
Die Proportionalit tskonstante, auch bekannt als die Konstante des Viscose Kraft ($b$), h ngt im Allgemeinen von der Form des Objekts und der Viskosit t des Mediums ab, in dem es sich bewegt. Ein Beispiel f r diese Art von Kraft ist die, die von einem Fluidstrom auf einen kugelf rmigen K rper ausge bt wird, deren mathematischer Ausdruck als Stokesches Gesetz bekannt ist.
Die Widerstandskraft wird in Abh ngigkeit von der Viskosit t des Fluids und der Geschwindigkeit der Kugel durch die Gleichung definiert:
Stokes hat den Widerstand, dem die Kugel ausgesetzt ist, explizit berechnet und festgestellt, dass die Viskosit t proportional zum Radius der Kugel und zu ihrer Geschwindigkeit ist, was zu folgender Gleichung f hrt:
Im Fall der Stokes-Kraft in die Viscose Kraft ($F_v$) wird diese mit die Konstante des Viscose Kraft ($b$) und die Geschwindigkeit ($v$) modelliert,
was einem Wert von die Konstante des Viscose Kraft ($b$) entspricht, der mit die Viskosität ($\eta$) und der Radio de la Gota ($r$) gleich ist
Die Kraft mit konstanter Masse ($F$) ist gleich die Schwerkraft ($F_g$) minus die Viscose Kraft ($F_v$), also:
Diese Beziehung erm glicht die Aufstellung der Bewegungsgleichung f r die Augenblickliche Beschleunigung ($a$) mit eine Träge Masse ($m_i$), die aufgrund der Schwerkraft der Erde mit die Gravitationsbeschleunigung ($g$) f llt, und mit eine Gravitationsmasse ($m_g$), in die Konstante des Viscose Kraft ($b$), wird sie die Form annehmen von:
Die Volumen einer Kugel ($V$) f r eine Kugel mit ein Radius einer Kugel ($r$) wird durch die folgende Formel berechnet:
Die Massen, die Newton in seinen Prinzipien verwendete, sind mit der Tr gheit der K rper verbunden, was zum Konzept von die Träge Masse ($m_i$) f hrt.
Das nach Newton benannte Gesetz, das die Kraft zwischen K rpern aufgrund ihrer Massen beschreibt, ist mit der Gravitation verbunden und wird daher als die Gravitationsmasse ($m_g$) bezeichnet.
Empirisch wurde festgestellt, dass beide Massen quivalent sind, und daher definieren wir
Einstein war derjenige, der diese Gleichheit in Frage stellte und von diesem Zweifel aus verstand, warum beide in seiner Gravitationstheorie "gleich erscheinen". In seinem Argument erkl rte Einstein, dass Massen den Raum verformen, und diese Raumverformung f hrt zu einer Ver nderung des Verhaltens von K rpern. Auf diese Weise erweisen sich die Massen als quivalent. Das revolution re Konzept der Raumkr mmung impliziert, dass selbst Licht, das keine Masse hat, von Himmelsk rpern beeinflusst wird, was der Gravitationstheorie von Newton widerspricht. Dies wurde experimentell durch die Untersuchung des Verhaltens von Licht w hrend einer Sonnenfinsternis nachgewiesen. In dieser Situation werden Lichtstrahlen aufgrund der Anwesenheit der Sonne abgelenkt, was es erm glicht, Sterne hinter ihr zu beobachten.
Mit dem Stokes-Modell wird der viskose Widerstand die Konstante des Viscose Kraft ($b$) berechnet, der von der Radio de la Gota ($r$) und die Umgebungsviskosität ($\eta$) abh ngt, wie folgt:
Dies f hrt dazu, dass die Viskositätszeit und träge Masse ($\tau_i$) und die Viskositätszeit und schwere Masse ($\tau_g$) gleiche Werte annehmen die Anpassungszeit ($\tau$), die mit die Dichte ($\rho$) wie folgt berechnet werden:
In einem Szenario horizontaler Bewegung steht die Kugel ausschlie lich einem Widerstand aufgrund der Viskosit t des umgebenden Mediums gegen ber, der durch die Gleichung mit die Geschwindigkeit ($v$), die Anfangsgeschwindigkeit ($v_0$), die Viskositätszeit und träge Masse ($\tau_i$) und der Zeit ($t$) quantifiziert werden kann:
Folglich f hrt die Interaktion zwischen diesen Elementen zur Beobachtung, dass die Komponente x der Geschwindigkeit ($v_x$) mit die Horizontale Geschwindigkeit ($v_{0x}$), die Anpassungszeit ($\tau$) und der Zeit ($t$) steht:
Im Kontext der horizontalen Bewegung wird die Position durch Integration der Geschwindigkeit erhalten, was zu einer Gleichung in die Position ($s$) mit die Ausgangsstellung ($s_0$), die Anfangsgeschwindigkeit ($v_0$), die Viskositätszeit und schwere Masse ($\tau_g$), die Viskositätszeit und träge Masse ($\tau_i$), die Gravitationsbeschleunigung ($g$) und der Zeit ($t$) f hrt:
Aus dieser Gleichung gelangen wir zur horizontalen Verschiebungsgleichung f r die Position auf der x-Achse ($x$) mit die Ausgangsposition auf der x-Achse ($x_0$), die Horizontale Geschwindigkeit ($v_{0x}$), die Anpassungszeit ($\tau$) und der Zeit ($t$):
Mit der Bewegungsgleichung eines K rpers in einem viskosen Medium haben wir die Ableitung von die Geschwindigkeit ($v$) bei der Zeit ($t$) mit die Konstante des Viscose Kraft ($b$) und die Gravitationsbeschleunigung ($g$):
Damit wird die Viskositätszeit und träge Masse ($\tau_i$) definiert als:
Im Kontext der vertikalen Bewegung steht die Kugel vor einem doppelten Widerstand: Einerseits die Viskosit t des umgebenden Mediums und andererseits die Schwerkraft, die sie nach unten zieht. Letztere kann durch die Gleichung in die Geschwindigkeit ($v$) mit die Anfangsgeschwindigkeit ($v_0$), die Viskositätszeit und schwere Masse ($\tau_g$), die Viskositätszeit und träge Masse ($\tau_i$), die Gravitationsbeschleunigung ($g$) und der Zeit ($t$) quantifiziert werden:
Angenommen, die gravitative Masse und die tr gheitsbedingte Masse sind identisch, dann erhalten wir die Funktion f r die Komponente y der Geschwindigkeit ($v_y$) mit die Vertikale Geschwindigkeit ($v_{0y}$), die Anpassungszeit ($\tau$), die Gravitationsbeschleunigung ($g$) und der Zeit ($t$):
Im Szenario der vertikalen Bewegung wird die Position durch Integration der Geschwindigkeit erhalten, was zu einer Gleichung in die Position ($s$) mit die Ausgangsstellung ($s_0$), die Anfangsgeschwindigkeit ($v_0$), die Viskositätszeit und schwere Masse ($\tau_g$), die Viskositätszeit und träge Masse ($\tau_i$), die Gravitationsbeschleunigung ($g$) und der Zeit ($t$) f hrt:
Aus dieser Gleichung ergibt sich die Gleichung f r die vertikale Verschiebung f r die Position auf der y-Achse ($y$) mit die Ausgangsposition auf der y-Achse ($y_0$), die Horizontale Geschwindigkeit ($v_{0x}$), die Anpassungszeit ($\tau$) und der Zeit ($t$):
ID:(1964, 0)