Fuerza de Stokes
Storyboard 
Un ejemplo de fuerza viscosa es el modelo desarrollado cuando una esfera se desplaza en un medio viscoso. Este modelo y la ecuación correspondiente se conocen por el nombre de su autor, George Stokes.La fuerza de Stokes está condicionada por la viscosidad del medio, el radio de la esfera y la velocidad a la que se mueve en el medio. De manera similar, si el medio se desplaza, arrastra el objeto junto con él.
ID:(1964, 0)
George Stokes
Descripción 
George Stokes realizó numerosos trabajos en hidrodinámica y matemáticas, siendo principalmente recordado por la conocida ley de Stokes aplicada a cuerpos esféricos en un flujo y por el teorema de Stokes en matemáticas.

George Gabriel Stokes (1819-1903)
ID:(12535, 0)
Fuerzas sobre una esfera que cae en un medio
Descripción 
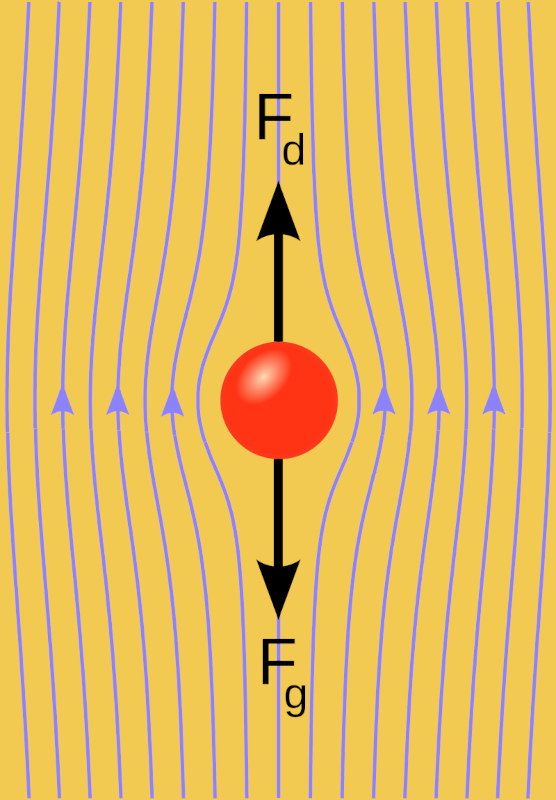
Cuando se arroja una esfera en un medio viscoso, aparece una fuerza ascendente inicial, una fuerza gravitacional ($F_g$), que comienza a hundir progresivamente el cuerpo. Durante este proceso, la esfera gana velocidad, dando lugar a una fuerza descendente, una fuerza viscosa ($F_v$), que depende de la velocidad. A medida que la velocidad total, la fuerza con masa constante ($F$),
| $ F = F_g - F_v $ |
comienza a reducirse hasta volverse nula. A partir de este momento, el movimiento continúa a una velocidad constante, ya que no hay fuerza que lo acelere.
ID:(15544, 0)
Fuerza de Stokes
Concepto 
La fuerza de Stokes es la fuerza generada por el flujo alrededor de una esfera de ERROR:6690,0 inmersa en él. En este caso, se utiliza el modelo de la fuerza proporcional a la velocidad ($v$):
| $ F_v = b v $ |
En este contexto, se puede demostrar que la constante de fuerza viscosa ($b$) con la viscosidad ($\eta$) es igual a:
| $ b \equiv 6 \pi \eta r $ |
por lo tanto, la fuerza de Stokes se expresa como:
| $ F_v =6 \pi \eta r v $ |
Esta fuerza se aplica principalmente en flujos laminares.
ID:(15555, 0)
Velocidad de caída en medio viscoso
Concepto 
El movimiento de una esfera en dos dimensiones se caracteriza por la componente x de la velocidad ($v_x$) con la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$):
| $ v_x = v_{0x} e^{- t / \tau }$ |
y la componente y de la velocidad ($v_y$) con la velocidad vertical inicial ($v_{0y}$), la tiempo de adaptación ($\tau$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$ |
que se representa en un diagrama $v_x$ vs $v_y$:
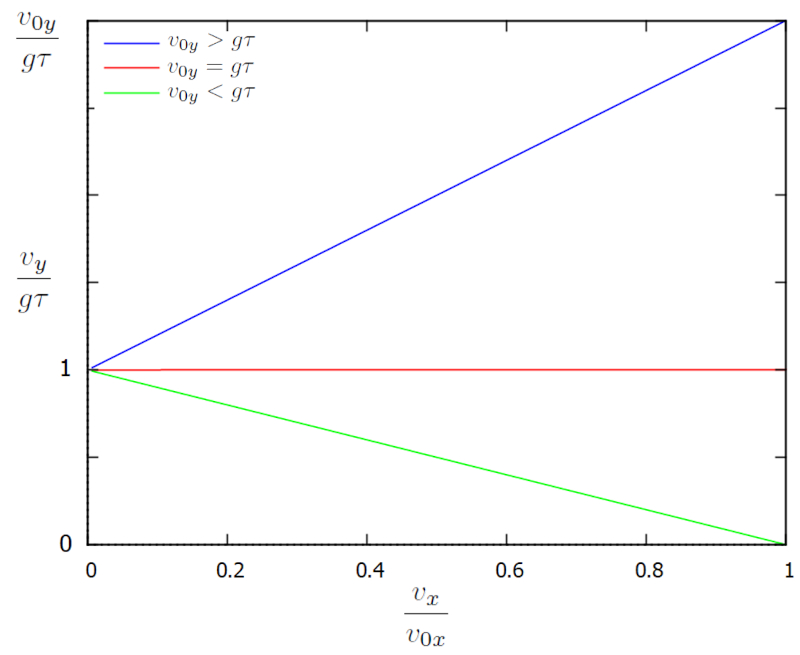
El diagrama muestra cómo ambas componentes de la velocidad evolucionan en el tiempo. Inicialmente, $v$ es igual a $v_{0x}$, lo que corresponde a un punto en el borde derecho del gráfico. Con el tiempo, las componentes de la velocidad evolucionan desde el lado derecho hasta el borde izquierdo, donde la velocidad horizontal es nula y la velocidad vertical llega al límite $g\tau$, por lo que $v/g\tau$ es igual a uno.
ID:(15558, 0)
Camino de caída en medio viscoso
Concepto 
El desplazamiento horizontal se puede calcular mediante la ecuación pour la posición en el eje x ($x$) con la posición inicial en el eje x ($x_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$) :
| $ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$ |
y el desplazamiento vertical de la posición en el eje y ($y$) con la posición inicial en el eje y ($y_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$) :
| $ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$ |
lo que se grafica en las posiciones $x$ vs $y$ :
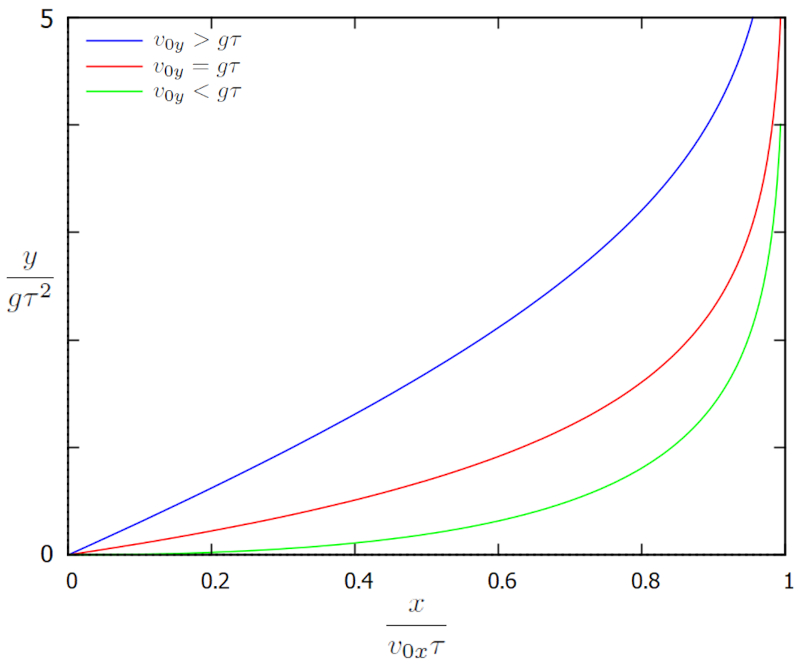
En este caso, la posición evoluciona desde el borde izquierdo hacia el derecho, donde se detiene en su movimiento horizontal alcanzando una distancia máxima de $v_{0x}\tau$. El desplazamiento vertical se describe con un sistema de coordenadas cuyo origen se encuentra en el punto donde comienza la trayectoria y que en su versión vertical apunta hacia abajo. En ese sentido, el incremento en $y$ corresponde al descenso de la esfera en la dirección de la gravedad.
ID:(15559, 0)
Método de Ostwald para medir viscosidad
Descripción 
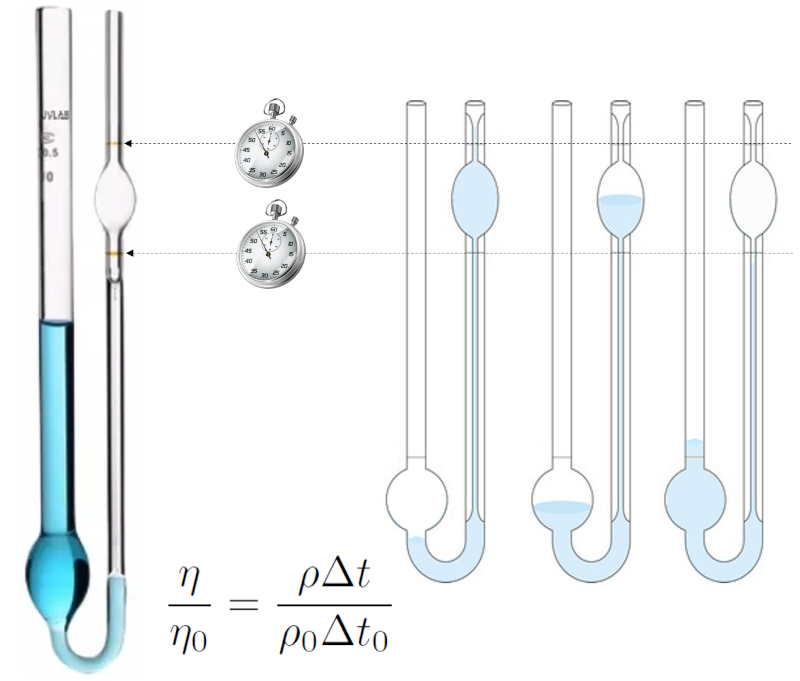
El método de medición de viscosidad de Ostwald se basa en el comportamiento de un líquido que fluye por un tubo de radio pequeño (capilar).
Se introduce el líquido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.
El experimento se realiza primero con un líquido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el líquido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el líquido que fluya en ambos casos será similar, y con ello, el tiempo será proporcional a la densidad dividida por la viscosidad. Así, se puede establecer una ecuación de comparación entre ambas viscosidades:
ID:(15545, 0)
Fuerza de Stokes
Modelo 
Un ejemplo de fuerza viscosa es el modelo desarrollado cuando una esfera se desplaza en un medio viscoso. Este modelo y la ecuación correspondiente se conocen por el nombre de su autor, George Stokes. La fuerza de Stokes está condicionada por la viscosidad del medio, el radio de la esfera y la velocidad a la que se mueve en el medio. De manera similar, si el medio se desplaza, arrastra el objeto junto con él.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3241)
(ID 3243)
Dado que el momento ($p$) se define con la masa inercial ($m_i$) y la velocidad ($v$),
| $ p = m_i v $ |
Si la masa inercial ($m_i$) es igual a la masa inicial ($m_0$), entonces podemos derivar el momento respecto al tiempo y obtener la fuerza con masa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Por lo tanto, llegamos a la conclusi n de que
| $ F = m_i a $ |
(ID 10975)
(ID 12552)
Si el tiempo caracter stico se define como
$\tau=\displaystyle\frac{m_i}{b}$
y el coeficiente de la fuerza viscosa es
$b=6\pi r\eta$
Por otro lado, dado que
| $ \rho \equiv\displaystyle\frac{ m_i }{ V }$ |
y
| $ V =\displaystyle\frac{4 \pi }{3} r ^3$ |
se tiene que la masa es
$m_i = \rho V = \displaystyle\frac{4\pi}{3} r^3 \rho$
lo que nos lleva a
$\tau = \displaystyle\frac{m_i}{b}=\displaystyle\frac{2 \rho r^2}{9\eta}$
en otras palabras,
| $\tau = \displaystyle\frac{2 r ^2 \rho }{9 \eta }$ |
(ID 14465)
(ID 15543)
Ejemplos
(ID 15540)
George Stokes realiz numerosos trabajos en hidrodin mica y matem ticas, siendo principalmente recordado por la conocida ley de Stokes aplicada a cuerpos esf ricos en un flujo y por el teorema de Stokes en matem ticas.

George Gabriel Stokes (1819-1903)
(ID 12535)
Cuando se arroja una esfera en un medio viscoso, aparece una fuerza ascendente inicial, una fuerza gravitacional ($F_g$), que comienza a hundir progresivamente el cuerpo. Durante este proceso, la esfera gana velocidad, dando lugar a una fuerza descendente, una fuerza viscosa ($F_v$), que depende de la velocidad. A medida que la velocidad total, la fuerza con masa constante ($F$),
| $ F = F_g - F_v $ |
comienza a reducirse hasta volverse nula. A partir de este momento, el movimiento contin a a una velocidad constante, ya que no hay fuerza que lo acelere.

(ID 15544)
La fuerza de Stokes es la fuerza generada por el flujo alrededor de una esfera de ERROR:6690,0 inmersa en l. En este caso, se utiliza el modelo de la fuerza proporcional a la velocidad ($v$):
| $ F_v = b v $ |
En este contexto, se puede demostrar que la constante de fuerza viscosa ($b$) con la viscosidad ($\eta$) es igual a:
| $ b \equiv 6 \pi \eta r $ |
por lo tanto, la fuerza de Stokes se expresa como:
| $ F_v =6 \pi \eta r v $ |
Esta fuerza se aplica principalmente en flujos laminares.
(ID 15555)
El movimiento de una esfera en dos dimensiones se caracteriza por la componente x de la velocidad ($v_x$) con la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$):
| $ v_x = v_{0x} e^{- t / \tau }$ |
y la componente y de la velocidad ($v_y$) con la velocidad vertical inicial ($v_{0y}$), la tiempo de adaptación ($\tau$), la aceleración gravitacional ($g$) y el tiempo ($t$):
| $ v_y = g \tau + ( v_{0y} - g \tau )e^{- t / \tau }$ |
que se representa en un diagrama $v_x$ vs $v_y$:

El diagrama muestra c mo ambas componentes de la velocidad evolucionan en el tiempo. Inicialmente, $v$ es igual a $v_{0x}$, lo que corresponde a un punto en el borde derecho del gr fico. Con el tiempo, las componentes de la velocidad evolucionan desde el lado derecho hasta el borde izquierdo, donde la velocidad horizontal es nula y la velocidad vertical llega al l mite $g\tau$, por lo que $v/g\tau$ es igual a uno.
(ID 15558)
El desplazamiento horizontal se puede calcular mediante la ecuaci n pour la posición en el eje x ($x$) con la posición inicial en el eje x ($x_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$) :
| $ x = x_0 + v_{0x} \tau (1 - e^{- t / \tau })$ |
y el desplazamiento vertical de la posición en el eje y ($y$) con la posición inicial en el eje y ($y_0$), la velocidad horizontal inicial ($v_{0x}$), la tiempo de adaptación ($\tau$) y el tiempo ($t$) :
| $ y = y_0 + \tau g t + \tau ( v_{0y} - g \tau )(1 - e^{- t / \tau })$ |
lo que se grafica en las posiciones $x$ vs $y$ :

En este caso, la posici n evoluciona desde el borde izquierdo hacia el derecho, donde se detiene en su movimiento horizontal alcanzando una distancia m xima de $v_{0x}\tau$. El desplazamiento vertical se describe con un sistema de coordenadas cuyo origen se encuentra en el punto donde comienza la trayectoria y que en su versi n vertical apunta hacia abajo. En ese sentido, el incremento en $y$ corresponde al descenso de la esfera en la direcci n de la gravedad.
(ID 15559)
El m todo de medici n de viscosidad de Ostwald se basa en el comportamiento de un l quido que fluye por un tubo de radio peque o (capilar).
Se introduce el l quido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.
El experimento se realiza primero con un l quido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el l quido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el l quido que fluya en ambos casos ser similar, y con ello, el tiempo ser proporcional a la densidad dividida por la viscosidad. As , se puede establecer una ecuaci n de comparaci n entre ambas viscosidades:

(ID 15545)
(ID 15542)
ID:(1964, 0)
