Fuerza viscosa y gravitación
Storyboard 
Cuando un cuerpo se desplaza en un medio viscoso bajo la influencia de una fuerza constante, como la gravedad, inicialmente la gravedad acelera el cuerpo hasta que su velocidad aumenta al punto en que la fuerza viscosa y la gravedad se equilibran. A partir de este punto, el cuerpo ya no experimenta aceleración y se desplaza a una velocidad constante.
ID:(1965, 0)
Fuerza viscosa sobre un cuerpo
Concepto 
La fuerza experimentada por un cuerpo que se desplaza con una velocidad de ERROR:6029.1 en un medio, y que está caracterizado por la constante de fuerza viscosa ($b$), es la fuerza viscosa ($F_v$), como se describe por la ecuación:
| $ F_v = b v $ |
Para comprender el papel de la constante de fuerza viscosa ($b$), es importante recordar que la viscosidad es una medida de cómo se difunde el momento, es decir, la velocidad de las moléculas. En otras palabras, la constante de fuerza viscosa ($b$) es la medida en la que el cuerpo pierde energía al transferirla al medio y al acelerar las moléculas, entregándoles energía. Por lo tanto, la constante de fuerza viscosa ($b$) es proporcional a la viscosidad.
ID:(15546, 0)
Fuerzas sobre una esfera que cae en un medio
Descripción 
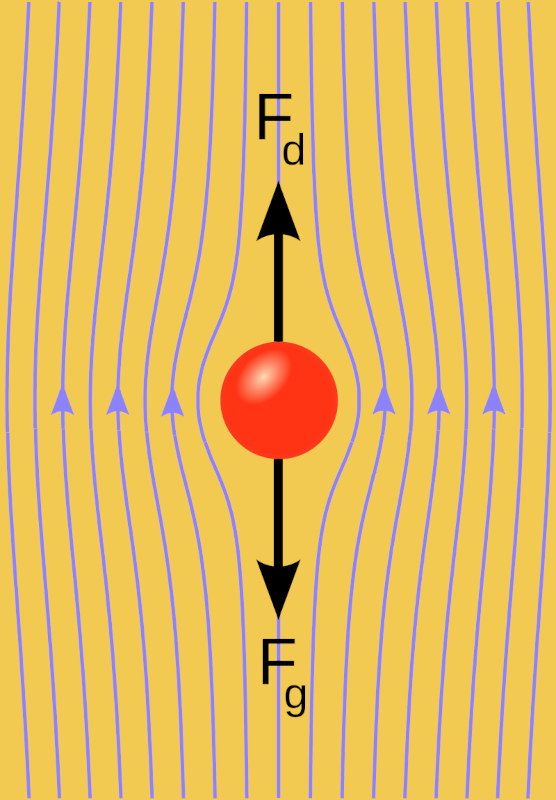
Cuando se arroja una esfera en un medio viscoso, aparece una fuerza ascendente inicial, una fuerza gravitacional ($F_g$), que comienza a hundir progresivamente el cuerpo. Durante este proceso, la esfera gana velocidad, dando lugar a una fuerza descendente, una fuerza viscosa ($F_v$), que depende de la velocidad. A medida que la velocidad total, la fuerza con masa constante ($F$),
| $ F = F_g - F_v $ |
comienza a reducirse hasta volverse nula. A partir de este momento, el movimiento continúa a una velocidad constante, ya que no hay fuerza que lo acelere.
ID:(15544, 0)
Método de Ostwald para medir viscosidad
Descripción 
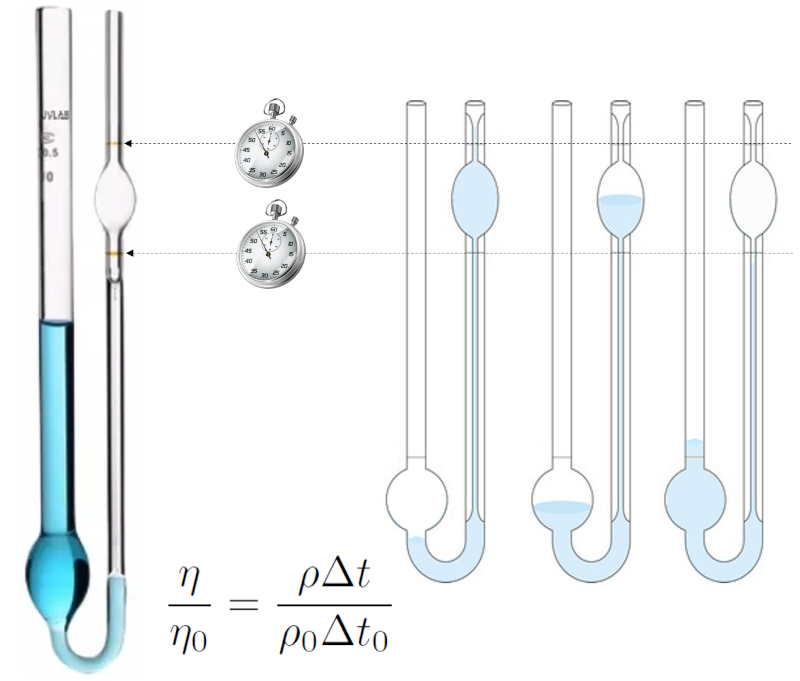
El método de medición de viscosidad de Ostwald se basa en el comportamiento de un líquido que fluye por un tubo de radio pequeño (capilar).
Se introduce el líquido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.
El experimento se realiza primero con un líquido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el líquido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el líquido que fluya en ambos casos será similar, y con ello, el tiempo será proporcional a la densidad dividida por la viscosidad. Así, se puede establecer una ecuación de comparación entre ambas viscosidades:
ID:(15545, 0)
Velocidad de caída en medio viscoso
Concepto 
En el caso de un cuerpo cayendo en un medio viscoso, la ecuación de movimiento es una ecuación de la velocidad ($v$) en función de el tiempo ($t$) con la masa gravitacional ($m_g$), la masa inercial ($m_i$), la aceleración gravitacional ($g$) y la constante de fuerza viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Esto se obtiene con la tiempo de viscosidad y masa inercial ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
y con la tiempo de viscosidad y masa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
Integrando con tiempo inicial nulo y la velocidad inicial ($v_0$),
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
que se representa a continuación:

El gráfico muestra cómo la viscosidad fuerza al cuerpo a descender con una velocidad asintótica ($v_{\infty}$), que es igual a $g\tau_g$. Esto ocurre en un tiempo del orden de la tiempo de viscosidad y masa inercial ($\tau_i$), tanto cuando la velocidad ($v$) es menor como mayor que la velocidad asintótica ($v_{\infty}$).
ID:(15547, 0)
Camino de caída en medio viscoso
Concepto 
En el caso de un cuerpo cayendo en un medio viscoso, la ecuación de movimiento es una ecuación de la posición ($s$) en función de la aceleración gravitacional ($g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la velocidad inicial ($v_0$) y el tiempo ($t$):
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
A partir desta equação, obtém-se integrando com tempo inicial zero e una posición inicial ($s_0$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
que se representa a continuación:

ID:(15550, 0)
Fuerza viscosa y gravitación
Modelo 
Cuando un cuerpo se desplaza en un medio viscoso bajo la influencia de una fuerza constante, como la gravedad, inicialmente la gravedad acelera el cuerpo hasta que su velocidad aumenta al punto en que la fuerza viscosa y la gravedad se equilibran. A partir de este punto, el cuerpo ya no experimenta aceleración y se desplaza a una velocidad constante.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 3241)
(ID 3243)
Dado que el momento ($p$) se define con la masa inercial ($m_i$) y la velocidad ($v$),
| $ p = m_i v $ |
Si la masa inercial ($m_i$) es igual a la masa inicial ($m_0$), entonces podemos derivar el momento respecto al tiempo y obtener la fuerza con masa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Por lo tanto, llegamos a la conclusi n de que
| $ F = m_i a $ |
(ID 10975)
(ID 12552)
La ecuaci n de movimiento en la velocidad ($v$) en el tiempo ($t$) con la masa inercial ($m_i$), la masa gravitacional ($m_g$), la aceleración gravitacional ($g$) y la constante de fuerza viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
junto con la definici n de la tiempo de viscosidad y masa inercial ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
y de la tiempo de viscosidad y masa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
puede ser reformulada como
$\displaystyle\frac{dv}{g\tau_g - v} = \displaystyle\frac{dt}{\tau_i}$
Si integramos esta expresi n entre una velocidad inicial ($v_0$) y la velocidad ($v$), y desde el tiempo inicial nulo hasta el tiempo ($t$), obtenemos
$\ln(g\tau_g-v_0)-\ln(g\tau_g-v)=\displaystyle\frac{t}{\tau_i}$
Resolviendo para la velocidad, obtenemos
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
(ID 14493)
(ID 15543)
Ejemplos
(ID 15539)
La fuerza experimentada por un cuerpo que se desplaza con una velocidad de ERROR:6029.1 en un medio, y que est caracterizado por la constante de fuerza viscosa ($b$), es la fuerza viscosa ($F_v$), como se describe por la ecuaci n:
| $ F_v = b v $ |
Para comprender el papel de la constante de fuerza viscosa ($b$), es importante recordar que la viscosidad es una medida de c mo se difunde el momento, es decir, la velocidad de las mol culas. En otras palabras, la constante de fuerza viscosa ($b$) es la medida en la que el cuerpo pierde energ a al transferirla al medio y al acelerar las mol culas, entreg ndoles energ a. Por lo tanto, la constante de fuerza viscosa ($b$) es proporcional a la viscosidad.
(ID 15546)
Cuando se arroja una esfera en un medio viscoso, aparece una fuerza ascendente inicial, una fuerza gravitacional ($F_g$), que comienza a hundir progresivamente el cuerpo. Durante este proceso, la esfera gana velocidad, dando lugar a una fuerza descendente, una fuerza viscosa ($F_v$), que depende de la velocidad. A medida que la velocidad total, la fuerza con masa constante ($F$),
| $ F = F_g - F_v $ |
comienza a reducirse hasta volverse nula. A partir de este momento, el movimiento contin a a una velocidad constante, ya que no hay fuerza que lo acelere.

(ID 15544)
El m todo de medici n de viscosidad de Ostwald se basa en el comportamiento de un l quido que fluye por un tubo de radio peque o (capilar).
Se introduce el l quido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.
El experimento se realiza primero con un l quido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el l quido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el l quido que fluya en ambos casos ser similar, y con ello, el tiempo ser proporcional a la densidad dividida por la viscosidad. As , se puede establecer una ecuaci n de comparaci n entre ambas viscosidades:

(ID 15545)
En el caso de un cuerpo cayendo en un medio viscoso, la ecuaci n de movimiento es una ecuaci n de la velocidad ($v$) en funci n de el tiempo ($t$) con la masa gravitacional ($m_g$), la masa inercial ($m_i$), la aceleración gravitacional ($g$) y la constante de fuerza viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Esto se obtiene con la tiempo de viscosidad y masa inercial ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
y con la tiempo de viscosidad y masa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
Integrando con tiempo inicial nulo y la velocidad inicial ($v_0$),
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
que se representa a continuaci n:

El gr fico muestra c mo la viscosidad fuerza al cuerpo a descender con una velocidad asintótica ($v_{\infty}$), que es igual a $g\tau_g$. Esto ocurre en un tiempo del orden de la tiempo de viscosidad y masa inercial ($\tau_i$), tanto cuando la velocidad ($v$) es menor como mayor que la velocidad asintótica ($v_{\infty}$).
(ID 15547)
En el caso de un cuerpo cayendo en un medio viscoso, la ecuaci n de movimiento es una ecuaci n de la posición ($s$) en funci n de la aceleración gravitacional ($g$), la tiempo de viscosidad y masa inercial ($\tau_i$), la tiempo de viscosidad y masa gravitacional ($\tau_g$), la velocidad inicial ($v_0$) y el tiempo ($t$):
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
A partir desta equa o, obt m-se integrando com tempo inicial zero e una posición inicial ($s_0$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
que se representa a continuaci n:

(ID 15550)
(ID 15541)
ID:(1965, 0)
