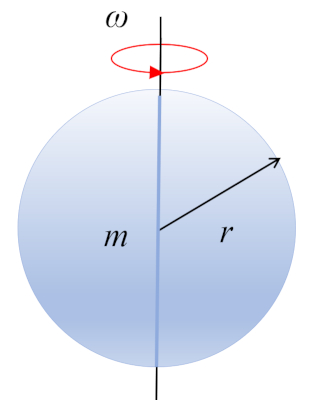
Trägheitsmoment einer Kugel
Storyboard 
Das Trägheitsmoment ist das rotatorische Äquivalent der Masse in der Translation. Im Fall einer Kugel, die um eine Achse rotiert, die durch ihr Zentrum verläuft, tritt der einfachste Fall auf, wenn die Rotation um das Massenzentrum stattfindet.
ID:(2088, 0)
Trägheitsmoment für eine Achse, die nicht durch den Massenschwerpunkt verläuft
Beschreibung 
Wenn die Rotationsachse nicht durch den Schwerpunkt (CM) verläuft, kann das Trägheitsmoment I mithilfe des Satzes von Steiner berechnet werden. Dazu beginnen wir mit dem Trägheitsmoment bezüglich des Schwerpunkts, zum Beispiel:
• Für einen Balken mit einer senkrechten Achse wird es berechnet
| I_{CM} =\displaystyle\frac{1}{12} m l ^2 |
• Für einen Zylinder mit einer senkrechten Achse wird es berechnet
| I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2) |
• Für einen Zylinder mit einer parallelen Achse wird es berechnet
| I_{CM} =\displaystyle\frac{1}{2} m r_c ^2 |
• Für ein Quader wird es berechnet
| I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2) |
• Für einen Würfel wird es berechnet
| I_{CM} =\displaystyle\frac{1}{6} m a ^2 |
• Für eine Kugel wird es berechnet
| I_{CM} =\displaystyle\frac{2}{5} m r_e ^2 |
Anschließend wird die Masse mit dem Quadrat des Abstands zwischen der Rotationsachse und dem Schwerpunkt multipliziert und addiert
| I = I_{CM} + m d ^2 |
ID:(15867, 0)
Application of Steiner's theorem to a sphere
Bild 
Für eine Kugel mit einer Achse in einer gewissen Entfernung von ihrem Zentrum:

dessen Trägheitsmoment bezüglich des Schwerpunkts (CM) wie folgt definiert ist: körpermasse kg, massenträgheitsmoment an der CM einer Kugel kg m^2 und radio der Kugel m
| I_{CM} =\displaystyle\frac{2}{5} m r_e ^2 |
kann das Trägheitsmoment mithilfe des Steiner'schen Satzes mit folgender Formel berechnet werden: entfernung Schwerpunkt und Achse m, körpermasse kg, trägheitsmoment für Achse, die nicht durch das CM verläuft kg m^2 und trägheitsmoment Massenzentrum kg m^2
| I = I_{CM} + m d ^2 |
.
ID:(11553, 0)
Modell
Top 
Parameter
Variablen
Berechnungen
Berechnungen
Berechnungen
Gleichungen
I = I_{CM} + m d ^2
I = I_CM + m * d ^ 2
I_{CM} =\displaystyle\frac{2}{5} m r_e ^2
I_CM = 2 * m * r_e ^ 2 / 5
\omega = \omega_0 + \alpha_0 ( t - t_0 )
omega = omega_0 + alpha_0 * ( t - t_0 )
T = I \alpha_0
T = I * alpha
T = r F
T = r * F
\theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2
theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2
\theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }
theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )
ID:(15861, 0)
Trägheitsmoment einer Kugel
Gleichung 
Das Trägheitsmoment einer Kugel, die sich um eine Achse dreht, die durch ihr Zentrum verläuft, wird durch die Segmentierung des Körpers in kleine Volumeneinheiten und deren Addition gewonnen:
| I =\displaystyle\int_V r ^2 \rho dV |
was zu folgendem Ergebnis führt:
.
ID:(4436, 0)
Steiner Satz
Gleichung 
Der Trägheitsmoment für Achse, die nicht durch das CM verläuft (I) kann berechnet werden, indem der Trägheitsmoment Massenzentrum (I_{CM}) verwendet und das Trägheitsmoment von die Körpermasse (m) als Punktmasse bei die Entfernung Schwerpunkt und Achse (d) hinzugefügt wird:
ID:(3688, 0)
Einfache Drehmoment-Kraft-Beziehung
Gleichung 
Da das Verhältnis zwischen dem Drehimpuls und dem Moment wie folgt ist:
| L = r p |
führt uns die zeitliche Ableitung zu der Beziehung des Drehmoments
Si se deriva en el tiempo la relación para el momento angular
| L = r p |
para el caso de que el radio sea constante
T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF
por lo que
| T = r F |
Die Drehung des Körpers erfolgt um eine Achse in Richtung des Drehmoments, das durch den Schwerpunkt verläuft.
ID:(4431, 0)
Drehmoment für konstantes Trägheitsmoment
Gleichung 
Im Fall, dass das Trägheitsmoment konstant ist, ist die Ableitung des Drehimpulses gleich
| L = I \omega |
was bedeutet, dass das Drehmoment gleich ist
Da das Moment gleich ist
| L = I \omega |
folgt daraus, dass im Fall, dass sich das Trägheitsmoment nicht mit der Zeit ändert,
T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha
was bedeutet, dass
| T = I \alpha |
.
Diese Beziehung entspricht dem Äquivalent des zweiten Newtonschen Gesetzes für Rotation anstelle von Translation.
ID:(3253, 0)
Winkelgeschwindigkeit mit konstanter Winkelbeschleunigung
Gleichung 
Mit die Constant Angular Acceleration (\alpha_0) stellt die Winkelgeschwindigkeit (\omega) eine lineare Beziehung mit der Zeit (t) her, die auch die Variablen die Anfängliche Winkelgeschwindigkeit (\omega_0) und der Startzeit (t_0) einbezieht, wie folgt:
Wenn wir annehmen, dass die Mittlere Winkelbeschleunigung (\bar{\alpha}) konstant und gleich die Constant Angular Acceleration (\alpha_0) ist, dann gilt die folgende Gleichung:
| \bar{\alpha} = \alpha_0 |
Daher, unter Berücksichtigung von die Unterschied in der Winkelgeschwindigkeiten (\Delta\omega) zusammen mit die Winkelgeschwindigkeit (\omega) und die Anfängliche Winkelgeschwindigkeit (\omega_0):
| \Delta\omega = \omega - \omega_0 |
und der Abgelaufene Zeit (\Delta t) in Bezug auf der Zeit (t) und der Startzeit (t_0):
| \Delta t \equiv t - t_0 |
kann die Gleichung für die Mittlere Winkelbeschleunigung (\bar{\alpha}):
| \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t } |
wie folgt ausgedrückt werden:
\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}
Durch Auflösen erhalten wir:
| \omega = \omega_0 + \alpha_0 ( t - t_0 ) |
Diese Gleichung repräsentiert eine Gerade im Raum der Winkelgeschwindigkeit gegenüber der Zeit.
ID:(3237, 0)
Angulo bei Konstanter Winkelbeschleunigung
Gleichung 
Da der gesamte Weg der Fläche unter der Kurve der Winkelgeschwindigkeit gegenüber der Zeit entspricht, ergibt sich im Fall von eine Constant Angular Acceleration (\alpha_0), dass der Weg der Winkel (\theta) mit den Variablen der Anfangswinkel (\theta_0), der Zeit (t), der Startzeit (t_0) und die Anfängliche Winkelgeschwindigkeit (\omega_0) wie folgt ist:
Im Fall von die Constant Angular Acceleration (\alpha_0) folgt die Winkelgeschwindigkeit (\omega) als Funktion von der Zeit (t) einer linearen Beziehung mit der Startzeit (t_0) und die Anfängliche Winkelgeschwindigkeit (\omega_0) in der Form:
| \omega = \omega_0 + \alpha_0 ( t - t_0 ) |
Da der zurückgelegte Winkel gleich der Fläche unter der Kurve der Winkelgeschwindigkeit-Zeit ist, kann in diesem Fall der Beitrag des Rechtecks:
\omega_0(t-t_0)
und des Dreiecks:
\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2
hinzugefügt werden.
Dies führt uns zu dem Ausdruck für der Winkel (\theta) und der Anfangswinkel (\theta_0):
| \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2 |
Diese Ausdruck entspricht der allgemeinen Form einer Parabel.
ID:(3682, 0)
Bremswinkel als Funktion der Winkelgeschwindigkeit
Gleichung 
Im Fall von die Constant Angular Acceleration (\alpha_0) wird die Funktion von die Winkelgeschwindigkeit (\omega) bezüglich der Zeit (t), zusammen mit den zusätzlichen Variablen die Anfängliche Winkelgeschwindigkeit (\omega_0) und der Startzeit (t_0), durch die Gleichung ausgedrückt:
| \omega = \omega_0 + \alpha_0 ( t - t_0 ) |
Aus dieser Gleichung lässt sich die Beziehung zwischen der Winkel (\theta) und der Anfangswinkel (\theta_0) sowie die Veränderung der Winkelgeschwindigkeit berechnen:
Wenn wir die Zeit in der Gleichung von die Winkelgeschwindigkeit (\omega) auflösen, die die Variablen die Anfängliche Winkelgeschwindigkeit (\omega_0), der Zeit (t), der Startzeit (t_0) und die Constant Angular Acceleration (\alpha_0) umfasst:
| \omega = \omega_0 + \alpha_0 ( t - t_0 ) |
erhalten wir den folgenden Ausdruck für die Zeit:
t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}
Diese Lösung kann in die Gleichung eingesetzt werden, um der Winkel (\theta) unter Verwendung von der Anfangswinkel (\theta_0) wie folgt zu berechnen:
| \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2 |
was in der folgenden Gleichung resultiert:
| \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 } |
ID:(4386, 0)