User:
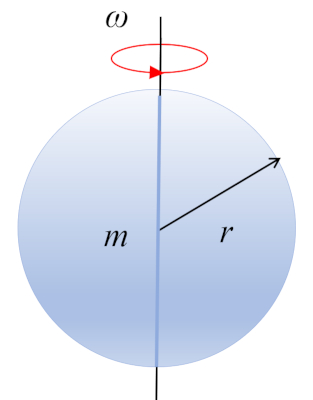
Moment of inertia of a sphere
Storyboard 
The moment of inertia is the rotational equivalent of mass in translational motion. In the case of a sphere rotating around an axis passing through its center, the simplest case occurs when the rotation takes place around the center of mass.
ID:(2088, 0)
Moment of inertia for an axis not passing through the center of mass
Description
When the axis of rotation does not pass through the center of mass (CM), the moment of inertia $I$ can be calculated using the Steiner's Theorem. To do this, we start with the moment of inertia with respect to the center of mass, for example:
• For a bar with a perpendicular axis, it is calculated
| $ I_{CM} =\displaystyle\frac{1}{12} m l ^2$ |
• For a cylinder with a perpendicular axis, it is calculated
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
• For a cylinder with a parallel axis, it is calculated
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
• For a parallelepiped, it is calculated
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
• For a cube, it is calculated
| $ I_{CM} =\displaystyle\frac{1}{6} m a ^2$ |
• For a sphere, it is calculated
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
Then, the product of mass and the square of the distance between the axis of rotation and the center of mass is added using
| $ I = I_{CM} + m d ^2$ |
ID:(15867, 0)
Application of Steiner's theorem to a sphere
Image
For a sphere with an axis at a distance from its center:
whose moment of inertia about the center of mass (CM) is defined as body mass $kg$, moment of Inertia at the CM of a Sphere $kg m^2$ and radio of the Sphere $m$
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
the calculation of the moment of inertia can be carried out using the Steiner's theorem with the following formula body mass $kg$, distance Center of Mass and Axis $m$, moment of inertia for axis that does not pass through the CM $kg m^2$ and moment of Inertia Mass Center $kg m^2$
| $ I = I_{CM} + m d ^2$ |
.
ID:(11553, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ I = I_{CM} + m d ^2$
I = I_CM + m * d ^ 2
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ \omega = \omega_0 + \alpha_0 ( t - t_0 )$
omega = omega_0 + alpha_0 * ( t - t_0 )
$ T = I \alpha_0 $
T = I * alpha
$ T = r F $
T = r * F
$ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$
theta = theta_0 + omega_0 *( t - t_0 )+ alpha_0 *( t - t_0 )^2/2
$ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$
theta = theta_0 +( omega ^2 - omega_0 ^2)/(2* alpha_0 )
ID:(15861, 0)
Moment of inertia of a sphere
Equation
The moment of inertia of a sphere rotating around an axis passing through its center is obtained by segmenting the body into small volumes and summing:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
.
ID:(4436, 0)
Steiner theorem
Equation
The moment of inertia for axis that does not pass through the CM ($I$) can be calculated using the moment of Inertia Mass Center ($I_{CM}$) and adding the moment of inertia of the body mass ($m$) as if it were a point mass at the distance Center of Mass and Axis ($d$):
| $ I = I_{CM} + m d ^2$ |
ID:(3688, 0)
Simple torque - force relationship
Equation
Since the relationship between angular momentum and torque is
| $ L = r p $ |
its temporal derivative leads us to the torque relationship
| $ T = r F $ |
Si se deriva en el tiempo la relación para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
The body's rotation occurs around an axis in the direction of the torque, which passes through the center of mass.
ID:(4431, 0)
Torque for constant moment of inertia
Equation
In the case where the moment of inertia is constant, the derivative of angular momentum is equal to
| $ L = I \omega $ |
which implies that the torque is equal to
| $ T = I \alpha_0 $ |
| $ T = I \alpha $ |
Since the moment is equal to
| $ L = I \omega $ |
it follows that in the case where the moment of inertia doesn't change with time,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
which implies that
| $ T = I \alpha $ |
.
This relationship is the equivalent of Newton's second law for rotation instead of translation.
ID:(3253, 0)
Angular velocity with constant angular acceleration
Equation
With the constant Angular Acceleration ($\alpha_0$), the angular Speed ($\omega$) forms a linear relationship with the time ($t$), incorporating the variables the initial Angular Speed ($\omega_0$) and the start Time ($t_0$) as follows:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
If we assume that the mean Angular Acceleration ($\bar{\alpha}$) is constant, equivalent to the constant Angular Acceleration ($\alpha_0$), then the following equation applies:
| $ \bar{\alpha} = \alpha_0 $ |
Therefore, considering the difference in Angular Speeds ($\Delta\omega$) along with the angular Speed ($\omega$) and the initial Angular Speed ($\omega_0$):
| $ \Delta\omega = \omega - \omega_0 $ |
and the time elapsed ($\Delta t$) in relation to the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
the equation for the mean Angular Acceleration ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
can be expressed as:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Solving this, we obtain:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
This equation represents a straight line in the angular velocity versus time plane.
ID:(3237, 0)
Angle at Constant Angular Acceleration
Equation
Given that the total displacement corresponds to the area under the angular velocity versus time curve, in the case of a constant Angular Acceleration ($\alpha_0$), it is determined that the displacement the angle ($\theta$) with the variables the initial Angle ($\theta_0$), the time ($t$), the start Time ($t_0$), and the initial Angular Speed ($\omega_0$) is as follows:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
In the case of the constant Angular Acceleration ($\alpha_0$), the angular Speed ($\omega$) as a function of the time ($t$) follows a linear relationship with the start Time ($t_0$) and the initial Angular Speed ($\omega_0$) in the form of:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Given that the angular displacement is equal to the area under the angular velocity-time curve, in this case, one can add the contributions of the rectangle:
$\omega_0(t-t_0)$
and the triangle:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
This leads us to the expression for the angle ($\theta$) and the initial Angle ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
This expression corresponds to the general form of a parabola.
ID:(3682, 0)
Braking angle as a function of angular velocity
Equation
In the case of the constant Angular Acceleration ($\alpha_0$), the function of the angular Speed ($\omega$) with respect to the time ($t$), along with additional variables the initial Angular Speed ($\omega_0$) and the start Time ($t_0$), is expressed by the equation:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
From this equation, it is possible to calculate the relationship between the angle ($\theta$) and the initial Angle ($\theta_0$), as well as the change in angular velocity:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
If we solve for time in the equation of the angular Speed ($\omega$) that includes the variables the initial Angular Speed ($\omega_0$), the time ($t$), the start Time ($t_0$), and the constant Angular Acceleration ($\alpha_0$):
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
we obtain the following expression for time:
$t - t_0 = \displaystyle\frac{\omega - \omega_0}{\alpha_0}$
This solution can be substituted into the equation to calculate the angle ($\theta$) using the initial Angle ($\theta_0$) as follows:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
which results in the following equation:
| $ \theta = \theta_0 +\displaystyle\frac{ \omega ^2- \omega_0 ^2}{2 \alpha_0 }$ |
ID:(4386, 0)