Utilisateur:
Énergie cinétique totale
Storyboard 
L'énergie cinétique totale est la somme de l'énergie cinétique de translation et de l'énergie cinétique de rotation.
Cette distinction est importante car selon la manière dont un objet se déplace, l'énergie cinétique peut être distribuée différemment entre la translation et la rotation, ce qui affecte la vitesse à laquelle il se déplace.
ID:(1418, 0)
Cylindre qui tourne autour de l'axe $\parallel$
Image
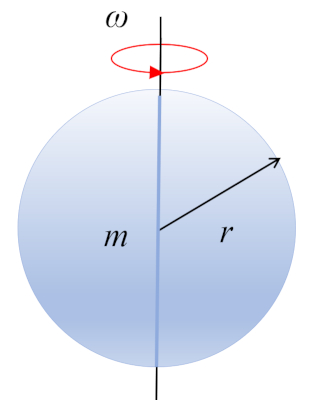
Considérons une rotation d'un cylindre de masse $m$ et de rayon $r$ autour de l'axe du cylindre, où le centre de masse (CM) se situe à mi-hauteur :
ID:(10964, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$
I_CM = m * r_c ^2/2
$ K = K_t + K_r $
K = K_t + K_r
$ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$
K = m * v ^2/2+ I * omega ^2/2
$ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$
K =( m + I / r ^2) * v ^2/2
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
$ K_t =\displaystyle\frac{1}{2} m_i v ^2$
K_t = m_i * v ^2/2
ID:(15607, 0)
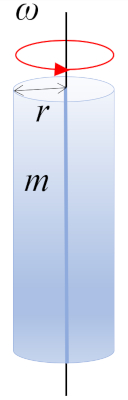
Moment d'inertie du cylindre, axe $\parallel$
Équation
Le moment d'inertie d'un cylindre en rotation autour d'un axe parallèle ($\parallel$) à son axe central est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui aboutit à
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
.
ID:(4434, 0)
Moment d'inertie d'une sphère
Équation
Le moment d'inertie d'une sphère en rotation autour d'un axe passant par son centre est obtenu en segmentant le corps en petits volumes et en les additionnant :
ce qui donne comme résultat :
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
.
ID:(4436, 0)
Énergie cinétique translationnelle
Équation
Dans le cas où l'on étudie la translation, la définition de l'énergie
| $ dW = \vec{F} \cdot d\vec{s} $ |
est appliquée au deuxième principe de Newton
| $ F = m_i a $ |
ce qui conduit à l'expression
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
L'énergie nécessaire pour qu'un objet passe de la vitesse $v_1$ à la vitesse $v_2$ peut être calculée en utilisant la définition avec
| $ dW = \vec{F} \cdot d\vec{s} $ |
Avec la deuxième loi de Newton, cette expression peut être réécrite comme
$\Delta W = m a \Delta s = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s$
En utilisant la définition de la vitesse avec
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
nous obtenons
$\Delta W = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s = m v \Delta v$
où la différence de vitesses est
$\Delta v = v_2 - v_1$
De plus, la vitesse elle-même peut être approximée par la vitesse moyenne
$v = \displaystyle\frac{v_1 + v_2}{2}$
En utilisant les deux expressions, nous obtenons l'expression
$\Delta W = m v \Delta v = m(v_2 - v_1)\displaystyle\frac{(v_1 + v_2)}{2} = \displaystyle\frac{m}{2}(v_2^2 - v_1^2)$
Ainsi, l'énergie varie comme
$\Delta W = \displaystyle\frac{m}{2}v_2^2 - \displaystyle\frac{m}{2}v_1^2$
Nous pouvons ainsi définir l'énergie cinétique
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
ID:(3244, 0)
Énergie cinétique de rotation
Équation
Dans le cas de l'étude de la translation, la définition de l'énergie
| $ \Delta W = T \Delta\theta $ |
est appliquée à la deuxième loi de Newton
| $ T = I \alpha $ |
ce qui conduit à l'expression
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
L'énergie nécessaire pour qu'un objet passe de la vitesse angulaire $\omega_1$ à la vitesse angulaire $\omega_2$ peut être calculée à l'aide de la définition
| $ \Delta W = T \Delta\theta $ |
Avec la deuxième loi de Newton, nous pouvons réécrire cette expression comme
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
En utilisant la définition de la vitesse angulaire
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
nous obtenons
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I,\omega,\Delta\omega$
La différence entre les vitesses angulaires est
$\Delta\omega=\omega_2-\omega_1$
D'autre part, la vitesse angulaire elle-même peut être approximée par la vitesse angulaire moyenne
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
En utilisant ces deux expressions, nous obtenons l'équation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Ainsi, l'énergie varie selon
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Nous pouvons utiliser cela pour définir l'énergie cinétique
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Énergie cinétique totale
Équation
L'énergie cinétique peut être de translation et/ou de rotation. Ainsi, l'énergie cinétique totale est la somme des deux :
| $ K = K_t + K_r $ |
ID:(3686, 0)
Énergie cinétique totale avec détai
Équation
L'énergie cinétique totale est calculée en additionnant les énergies cinétiques de translation et de rotation
| $ K = K_t + K_r $ |
donc nous avons:
| $ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
L'énergie cinétique totale
| $ K = K_t + K_r $ |
est la somme de l'énergie cinétique de translation
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
et de l'énergie cinétique de rotation
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
donc nous avons :
| $ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(9944, 0)
Énergie cinétique d'un objet roulant
Équation
Lorsqu'un objet roule,
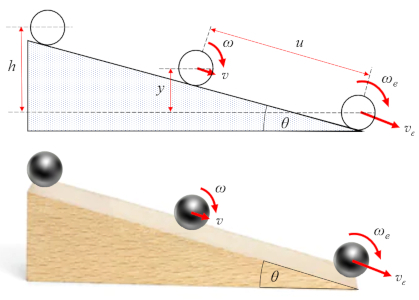
sa vitesse angulaire est reliée à sa vitesse de translation par
| $ v = r \omega $ |
ce qui entraîne l'énergie cinétique de rotation
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
et par conséquent, aboutit à une énergie cinétique totale
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
Lorsqu'un objet roule, sa vitesse angulaire est reliée à sa vitesse de translation par
| $ v = r \omega $ |
ce qui entraîne l'énergie cinétique de rotation
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
qui devient
$K_r=\displaystyle\frac{1}{2}I \omega^2=\displaystyle\frac{1}{2} I \displaystyle\frac{v^2}{r^2}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{I}{r^2}\right)v^2$
Ainsi, en combinant l'énergie cinétique de translation
l'énergie cinétique d'un corps en rotation est calculée par la somme
| $ K = K_t + K_r $ |
c'est-à-dire,
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
ID:(9877, 0)