User:
Total kinetic energy
Storyboard 
The total kinetic energy is the sum of the kinetic energy of translation and the kinetic energy of rotation.
This distinction is important because depending on how an object moves, the kinetic energy can be distributed differently between translation and rotation, affecting the speed at which it moves.
ID:(1418, 0)
Cylinder rotating around axis $\parallel$
Image
A rotation of a cylinder with mass $m$ and radius $r$ around the axis of the cylinder, where the center of mass (CM) is located at mid-height:
ID:(10964, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$
I_CM = 2 * m * r_e ^ 2 / 5
$ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$
I_CM = m * r_c ^2/2
$ K = K_t + K_r $
K = K_t + K_r
$ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$
K = m * v ^2/2+ I * omega ^2/2
$ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$
K =( m + I / r ^2) * v ^2/2
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
$ K_t =\displaystyle\frac{1}{2} m_i v ^2$
K_t = m_i * v ^2/2
ID:(15607, 0)
Cylinder moment of inertia, axis $\parallel$
Equation
The moment of inertia of a cylinder rotating around an axis parallel ($\parallel$) to its central axis is obtained by segmenting the body into small volumes and summing them:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
.
ID:(4434, 0)
Moment of inertia of a sphere
Equation
The moment of inertia of a sphere rotating around an axis passing through its center is obtained by segmenting the body into small volumes and summing:
| $ I =\displaystyle\int_V r ^2 \rho dV $ |
resulting in
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
.
ID:(4436, 0)
Translational Kinetic Energy
Equation
In the case of studying translational motion, the definition of energy
| $ dW = \vec{F} \cdot d\vec{s} $ |
is applied to Newton's second law
| $ F = m_i a $ |
resulting in the expression
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
The energy required for an object to transition from velocity $v_1$ to velocity $v_2$ can be calculated using the definition with
| $ dW = \vec{F} \cdot d\vec{s} $ |
Using the second law of Newton, this expression can be rewritten as
$\Delta W = m a \Delta s = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s$
Employing the definition of velocity with
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
we obtain
$\Delta W = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s = m v \Delta v$
where the difference in velocities is
$\Delta v = v_2 - v_1$
Furthermore, the velocity itself can be approximated by the average velocity
$v = \displaystyle\frac{v_1 + v_2}{2}$
Using both expressions, we arrive at
$\Delta W = m v \Delta v = m(v_2 - v_1)\displaystyle\frac{(v_1 + v_2)}{2} = \displaystyle\frac{m}{2}(v_2^2 - v_1^2)$
Thus, the change in energy is given by
$\Delta W = \displaystyle\frac{m}{2}v_2^2 - \displaystyle\frac{m}{2}v_1^2$
In this way, we can define kinetic energy
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
ID:(3244, 0)
Kinetic Energy of Rotation
Equation
In the case being studied of translational motion, the definition of energy
| $ \Delta W = T \Delta\theta $ |
is applied to Newton's second law
| $ T = I \alpha $ |
resulting in the expression
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
The energy required for an object to change its angular velocity from $\omega_1$ to $\omega_2$ can be calculated using the definition
| $ \Delta W = T \Delta\theta $ |
Applying Newton's second law, this expression can be rewritten as
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Using the definition of angular velocity
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
we get
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
The difference in angular velocities is
$\Delta\omega=\omega_2-\omega_1$
On the other hand, angular velocity itself can be approximated with the average angular velocity
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Using both expressions, we obtain the equation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Thus, the change in energy is given by
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
This allows us to define kinetic energy as
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Total Kinetic Energy
Equation
Kinetic energy can be of translation and/or rotation. Therefore, the total kinetic energy is the sum of both:
| $ K = K_t + K_r $ |
ID:(3686, 0)
Total kinetic energy with detail
Equation
The total kinetic energy is calculated by adding the kinetic energies of translation and rotation
| $ K = K_t + K_r $ |
so we have:
| $ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
The total kinetic energy
| $ K = K_t + K_r $ |
is the sum of the translational kinetic energy
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
and the rotational kinetic energy
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
so we have:
| $ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(9944, 0)
Kinetic energy of a rolling object
Equation
When an object rolls,
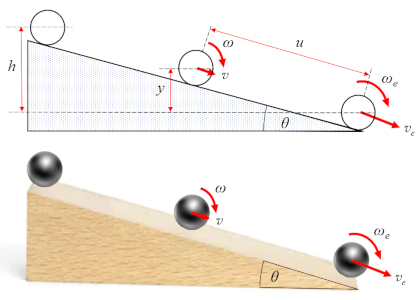
its angular velocity is related to its translational velocity by
| $ v = r \omega $ |
resulting in the rotational kinetic energy
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
and consequently, yielding a total kinetic energy
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
When an object rolls, its angular velocity is related to its translational velocity by
| $ v = r \omega $ |
resulting in the rotational kinetic energy
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
which becomes
$K_r=\displaystyle\frac{1}{2}I \omega^2=\displaystyle\frac{1}{2} I \displaystyle\frac{v^2}{r^2}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{I}{r^2}\right)v^2$
Thus, when combining the translational kinetic energy
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
the kinetic energy of a rotating body is calculated by the sum
| $ K = K_t + K_r $ |
meaning,
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
ID:(9877, 0)