Usuario:
Aceleración angular instantanea
Storyboard 
Para describir cómo evoluciona la velocidad angular en el tiempo, es necesario estudiar su variación a lo largo del tiempo.
La relación de la variación de la velocidad angular equivale al cambio en la velocidad angular en el tiempo transcurrido, que al dividirse por este, corresponde a la aceleración angular.
Para un intervalo de tiempo infinitesimal, la aceleración angular corresponde a la aceleración angular instantánea.
ID:(1452, 0)
Velocidad angular como integral de la aceleración
Nota
La integral de una función corresponde al área bajo la curva que define dicha función. Por lo tanto, la integral de la aceleración angular entre los tiempos $t_0$ y $t$ corresponde a la variación de la velocidad angular entre la velocidad angular inicial $\omega_0$ y $\omega$.
Por lo tanto, utilizando aceleración angular instantánea $rad/s^2$, tiempo $s$, tiempo inicial $s$, velocidad angular $rad/s$ y velocidad angular inicial $rad/s$, obtenemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Lo cual se muestra en el siguiente gráfico:
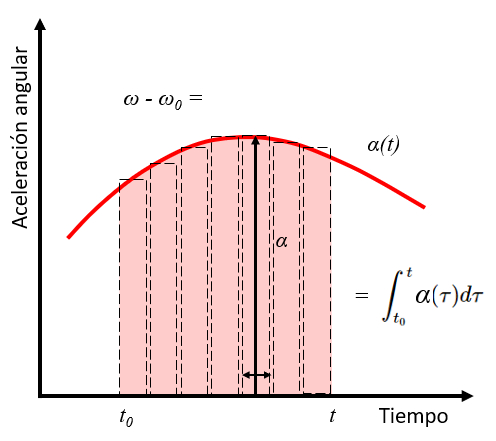
ID:(11415, 0)
Aceleración angular instantanea
Descripción
Para describir cómo evoluciona la velocidad angular en el tiempo, es necesario estudiar su variación a lo largo del tiempo. La relación de la variación de la velocidad angular equivale al cambio en la velocidad angular en el tiempo transcurrido, que al dividirse por este, corresponde a la aceleración angular. Para un intervalo de tiempo infinitesimal, la aceleración angular corresponde a la aceleración angular instantánea.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Dado que la aceleraci n tangencial es
| $ a = r \alpha $ |
Si el versor del eje es $\hat{n}$ y el radial es $\hat{r}$, el versor tangencial puede calcularse mediante el producto cruz:
$\hat{t} = \hat{n} \times \hat{r}$
En consecuencia, considerando que
$\vec{a} = a \hat{t}$
,
$\vec{r} = r \hat{r}$
y
$\vec{\alpha} = \alpha \hat{n}$
,
podemos deducir que
$\vec{a} = a \hat{t} = a \hat{n} \times \hat{r} = r \alpha \hat{n} \times \hat{r} = \vec{\alpha} \times \vec{r}$
,
lo que se traduce en
| $ \vec{a} = \vec{\alpha} \times \vec{r} $ |
(ID 11598)
Ejemplos
(ID 15415)
Si se toma un intervalo de tiempo $t$ con una velocidad angular $\omega(t)$ y se observa un punto en un momento futuro $t+\Delta t$ con una velocidad angular $\omega(t+\Delta t)$, la aceleraci n angular puede estimarse como la variaci n
$\omega(t+\Delta t)-\omega(t)$
en el transcurso del tiempo $\Delta t$:
$\alpha\sim\displaystyle\frac{\omega(t+\Delta t)-\omega(t)}{\Delta t}$
A medida que el valor de $\Delta t$ disminuye, la aceleraci n toma el papel de la tangente a la curva de velocidad en ese momento:
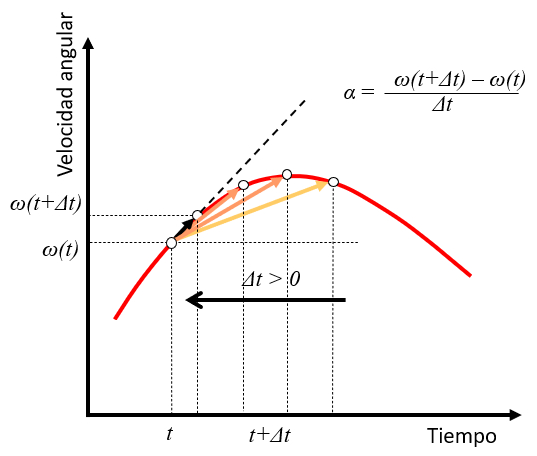
Esto generaliza lo que ya se ha visto en el caso de la aceleraci n angular constante.
(ID 11413)
La integral de una funci n corresponde al rea bajo la curva que define dicha funci n. Por lo tanto, la integral de la aceleraci n angular entre los tiempos $t_0$ y $t$ corresponde a la variaci n de la velocidad angular entre la velocidad angular inicial $\omega_0$ y $\omega$.
Por lo tanto, utilizando aceleración angular instantánea $rad/s^2$, tiempo $s$, tiempo inicial $s$, velocidad angular $rad/s$ y velocidad angular inicial $rad/s$, obtenemos:
| $ \omega = \omega_0 +\displaystyle\int_{t_0}^t \alpha\,d\tau $ |
Lo cual se muestra en el siguiente gr fico:
(ID 11415)
La direcci n de la aceleraci n tangencial puede determinarse utilizando la regla de la mano derecha, donde los dedos se orientan hacia el eje y luego se giran en direcci n al radio:
(ID 11600)
(ID 15426)
ID:(1452, 0)