Utilizador:
Fluxo turbulento através de tubos
Storyboard
Se o número de Reynolds exceder 2000, o fluxo em um tubo sempre se tornará instável e eventualmente se tornará completamente turbulento. Como resultado, não é mais possível usar a aproximação de fluxo laminar viscoso que dá origem à lei de Hagen-Poiseuille, sendo necessário desenvolver um modelo alternativo.
O modelo que descreve um fluxo no qual a viscosidade é irrelevante é aquele que origina a equação de Bernoulli. No entanto, esse modelo pressupõe que a densidade de energia seja conservada. Uma alternativa é assumir que a turbulência leva a uma mistura de tal forma que a densidade de energia não seja conservada, mas permaneça constante. Nesse caso, o fluxo pode ser modelado usando uma equação semelhante à de Bernoulli, mas com uma correção para levar em consideração a homogeneização devido aos efeitos de mistura.
ID:(1970, 0)
Modelagem de turbulência
Imagem
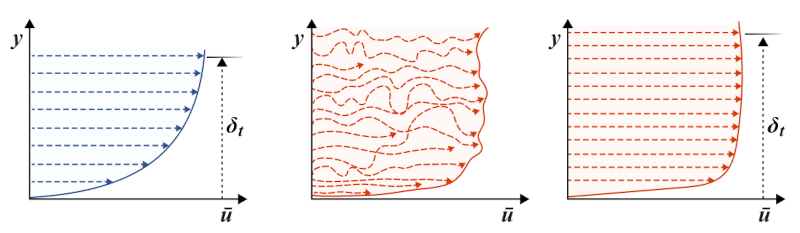
O fluxo laminar é descrito por "lâminas" que se movem a diferentes velocidades de forma coordenada. No entanto, no fluxo turbulento, essas "lâminas" não existem. Os elementos do fluido são desviados, podem mudar de direção e participar em movimentos circulares, frequentemente de forma caótica.
A primeira consequência disso é que os parâmetros do fluido tendem a se misturar, levando ao desaparecimento das diferenças de velocidade e à emergência de um tipo de velocidade média. Ao médio do movimento, surgem padrões estruturados, mas eles não mais originam-se dos elementos individuais do fluido, e sim de uma mistura temporal. Como resultado, obtemos novamente um perfil relativamente constante que se assemelha aos perfis definidos no fluxo laminar, mas nesse caso são valores médios e não apresentam grandes gradientes, tornando-os mais uniformes.
ID:(14525, 0)
Equação de Darcy-Weisbach
Equação
Quando modelamos o fluxo em um tubo, assumindo que a densidade de energia é conservada, obtemos a equação de Bernoulli, que neste caso descreve o fluxo da seguinte forma:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
onde $\Delta p$ é a diferença de pressão, $\rho$ é a densidade e $v$ é a velocidade.
No caso de fluxo turbulento, o processo de mistura atua como atrito, reduzindo o gradiente de velocidade que existe no fluxo laminar entre o centro e a borda do fluxo. Se assumirmos que esse fator de mistura pode ser modelado empiricamente com um fator de correção, chegamos empiricamente à equação de Darcy-Weisbach:
 $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w v ^2 $ |
onde $f_D$ é o fator de atrito de Darcy, $\Delta L$ é o comprimento e $D_H$ é o diâmetro hidráulico do tubo.
O fator de atrito foi obtido empiricamente para várias situações e é expresso como uma função do número de Reynolds.
ID:(14526, 0)
Diâmetro hidráulico
Equação
No caso da equação de Darcy-Weisbach, trabalhamos com um diâmetro hidráulico que corresponde a uma generalização do diâmetro tradicional de um círculo. Isso nos permite considerar uma seção não circular e calcular um diâmetro com base na área da seção, representada por $S$, e no seu perímetro, representado por $P$, utilizando a seguinte fórmula:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
No caso de uma seção circular, obtemos o diâmetro tradicional de um círculo da seguinte forma:
$D_H = \displaystyle\frac{4S}{P} = \displaystyle\frac{4\pi R^2}{2\pi R} = 2R$
ID:(14527, 0)
Raio hidráulico
Equação
No contexto do fator de atrito de Darcy-Weisbach, trabalhamos com um raio hidráulico que corresponde a uma generalização do raio tradicional de um círculo. Isso nos permite calcular um diâmetro com base na área da seção transversal $S$ e no seu perímetro em contato com o líquido $P$, utilizando a seguinte fórmula:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
Quando lidamos com uma seção circular, obtemos o raio hidráulico tradicional de um círculo da seguinte forma:
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
ID:(14531, 0)
Profundidade de um tubo vazio
Equação
Em um tubo cilíndrico, a profundidade depende do fluxo da seguinte forma:
Se integramos a seção transversal, podemos calcular como a área superficial depende da profundidade usando a seguinte equação:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Para fluxos pequenos, onde a profundidade é significativamente menor que o raio, a relação entre a seção e a profundidade simplifica-se consideravelmente. Ao resolver para a profundidade, obtemos:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
A área da seção transversal do tubo que contém o líquido pode ser integrada em relação à altura da seguinte maneira:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Se expandirmos essa expressão em termos do fator $h/R$ no limite $h\ll R$, obtemos, em primeira ordem:
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
Se resolvermos para a profundidade, obtemos finalmente:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
ID:(14541, 0)
Perímetro hidrodinâmico em tubo não preenchido
Equação
O perímetro hidrodinâmico de um tubo parcialmente cheio corresponde às bordas da seção em contato com o líquido, ou seja, o arco que toca a parede do tubo e a superfície:
Em geral, podemos expressar isso como:
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
Para fluxos pequenos, onde a profundidade é significativamente menor que o raio, isso simplifica a relação entre a seção e a profundidade para:
| $ P_H = \sqrt{2^5 R h }$ |
Dado que o ângulo pode ser determinado como:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
O arco é igual a $R\phi$, portanto, o comprimento total do arco é:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
Da mesma forma, metade da superfície pode ser determinada usando o teorema de Pitágoras, resultando em:
$\sqrt{2Rh - h^2}$
Assim, o perímetro hidrodinâmico é expresso como:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
No limite de uma altura pequena, onde $h\ll R$, esta expressão pode ser desenvolvida, resultando em:
| $ P_H = \sqrt{2^5 R h }$ |
ID:(14542, 0)
Diagrama Moody
Imagem
Em 1944, Lewis Ferry Moody mediu o fator de atrito de Darcy-Weisbach como função do número de Reynolds e da rugosidade relativa da parede, resultando na criação do seguinte diagrama:
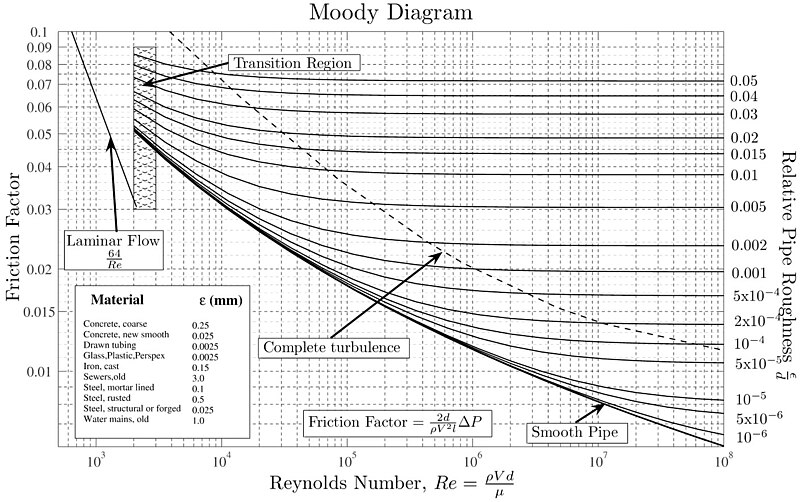
A rugosidade relativa pode ser estimada considerando o tamanho das irregularidades da superfície (altura de saliências ou profundidade de sulcos) em relação ao diâmetro hidráulico.
São observados dois comportamentos distintos:
• Para números de Reynolds abaixo de 2000, o fator de atrito de Darcy-Weisbach depende apenas do número de Reynolds, seguindo uma relação de $64/Re$. Isso corresponde ao regime de escoamento laminar.
• Para números de Reynolds acima de 2000, observa-se um comportamento que depende tanto do número de Reynolds quanto da rugosidade relativa da superfície do tubo.
ID:(14528, 0)
Limite laminar
Equação
No caso de baixos números de Reynolds, o diagrama de Moody mostra que o fator de atrito de Darcy-Weisbach, $f_D$, é igual a:
| $ f_D = \displaystyle\frac{64}{ Re }$ |
onde $Re$ é o número de Reynolds. Isso é válido para números de Reynolds até 2000. Além desse valor, a rugosidade da parede começa a afetar a desestabilização do fluxo e a formação de turbulências.
ID:(14529, 0)
Fluxo no limite laminar
Descrição
Se substituirmos o fator de atrito de Darcy-Weisbach no limite laminar, dado por
| $ f_D = \displaystyle\frac{64}{ Re }$ |
na equação de Darcy-Weisbach, representada como
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w v ^2 $ |
e usarmos a definição do número de Reynolds $Re$, podemos demonstrar que o fluxo é governado por
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
o que corresponde à equação de Hagen-Poiseuille.
ID:(14530, 0)
Equação de Colebrook-White em tubo fechado
Equação
No caso de o tubo estar completamente fechado, ou seja, o cilindro não possui uma abertura superior e o líquido preenche toda a seção, a equação de Colebrook-White
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{3.7 D_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
permite estimar o fator de atrito de Darcy-Weisbach em fluxo turbulento com base na rugosidade $\epsilon$, no diâmetro hidrodinâmico e no número de Reynolds.
ID:(14532, 0)
Solução para tubo fechado
Equação
A equação de Colebrook-White para o caso de um tubo fechado:
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{3.7 D_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
é uma equação implícita utilizada para determinar o fator de atrito de Darcy-Weisbach ($f_D$). Para resolver esta equação, foram desenvolvidas várias aproximações que variam em complexidade e precisão. Uma das aproximações mais eficazes, que abrange uma ampla faixa de números de Reynolds $Re$, é a proposta por S.E. Haaland:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
A solução original de S.E. Haaland é a seguinte:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/D_H}{3.7}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Pode ser rearranjada para obter a expressão do fator de atrito de Darcy-Weisbach $f_D$ da seguinte forma:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
ID:(14535, 0)
Equação de Colebrook-White em tubo aberto
Equação
Quando o tubo está aberto, ou seja, o líquido não preenche toda a seção do cilindro, a equação de Colebrook-White
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{12 R_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
permite estimar o fator de atrito de Darcy-Weisbach em fluxo turbulento com base na rugosidade $\epsilon$, no diâmetro hidráulico e no número de Reynolds.
ID:(14533, 0)
Solução para tubo aberto
Equação
A equação de Colebrook-White para o caso de um tubo fechado:
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{12 R_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
é uma equação implícita utilizada para determinar o fator de atrito de Darcy-Weisbach ($f_D$). Para resolver esta equação, foram desenvolvidas várias aproximações que variam em complexidade e precisão. Uma das aproximações mais eficazes, que abrange uma ampla faixa de números de Reynolds $Re$, é a proposta por S.E. Haaland:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
A solução original de S.E. Haaland é a seguinte:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/R_H}{12}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Pode ser rearranjada para obter a expressão do fator de atrito de Darcy-Weisbach $f_D$ da seguinte forma:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
ID:(14534, 0)
Perfil de velocidade de fluxo turbulento no tubo
Imagem
O perfil de velocidade do fluxo turbulento através de um tubo apresenta duas zonas distintas em função da distância à superfície ($z$), onde $\delta$ representa a espessura da camada limite. Na região próxima à superfície ($z < \delta$), o fluxo é essencialmente laminar, enquanto na região mais afastada da superfície ($z > \delta$), o fluxo se torna turbulento.
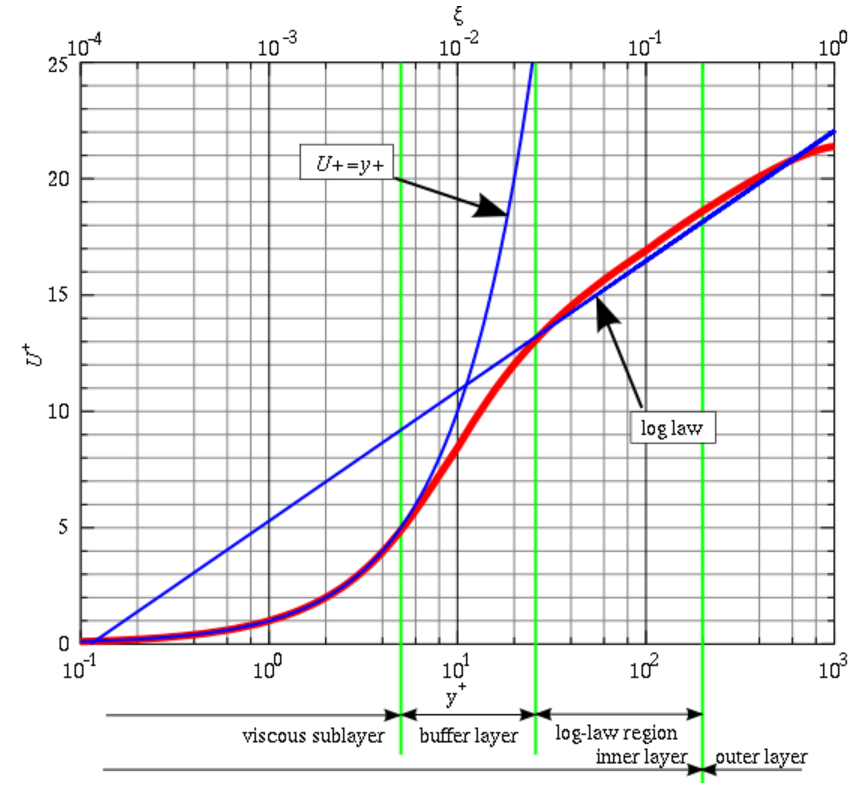
Na faixa laminar, a velocidade é proporcional à distância normalizada:
$u^+ = y^+$
Essa relação se assemelha ao perfil de velocidade de Hagen-Poiseuille próximo à parede e representa uma aproximação linear.
Na faixa turbulenta, o perfil de velocidade normalizado assume uma forma logarítmica:
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Aqui, $\kappa$ é a constante de Karman (aproximadamente $0.41$), e $y_0\sim 1/8$ é a distância normalizada na qual a velocidade seria zero. No entanto, é importante observar que a largura da camada laminar, conforme mostrado no gráfico, é aproximadamente 7,072 vezes maior do que $y_0$.
ID:(14536, 0)
Velocidade de corte
Equação
Dentro da camada limite laminar, o perfil de velocidade é dado por
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
o que, no limite das distâncias próximas à parede ($r \sim R$), nos permite definir a distância adimensional
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta} y$
e a velocidade adimensional
$u^+=\displaystyle\frac{u}{u_{\tau}}$
Ao normalizar esses valores, obtemos a lei logarítmica da velocidade turbulenta
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
No fluxo laminar, de acordo com Hagen Poiseuille, o perfil de velocidade é definido como:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
juntamente com a equação adicional:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Isso nos fornece uma relação para a velocidade em função da distância à parede:
$v=v_{max}\displaystyle\frac{2y}{R}=\displaystyle\frac{R}{2\eta}\displaystyle\frac{\Delta p}{\Delta L}y$
que corresponde à relação normalizada:
$u^+=y^+$
Quando consideramos a velocidade de cisalhamento $u_{\tau}$, a velocidade normalizada é expressa como:
$u^+=\displaystyle\frac{v}{u_{\tau}}$
e a distância à parede normalizada é:
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta} y$
Portanto, obtemos:
$u^+=\displaystyle\frac{v}{u_{\tau}}=\displaystyle\frac{R\Delta p}{2\eta\Delta L u_{\tau}}y=y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta}y$
o que nos leva a:
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
ID:(14538, 0)
Equação do perfil de velocidade do fluxo turbulento
Equação
Empiricamente, determinou-se que a velocidade no fluxo turbulento dentro de um tubo segue a seguinte forma:
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Usando a velocidade de cisalhamento
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
podemos descrever a velocidade no fluxo turbulento através de um tubo como:
| $ v_y = \displaystyle\frac{ u_{\tau} }{ \kappa }\ln\left(\displaystyle\frac{8 \rho_w u_{\tau} y }{ \eta }\right)$ |
De maneira empírica, determinou-se que a velocidade no fluxo turbulento dentro de um tubo segue a seguinte forma:
$u^+ = \displaystyle\frac{1}{\kappa} \ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Onde a velocidade normalizada é dada por:
$u^+=\displaystyle\frac{v}{u_{\tau}}$
E a distância normalizada em relação à parede é definida como:
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta}y$
Com a velocidade de cisalhamento fornecida por:
| $ u_{\tau} =\sqrt{\displaystyle\frac{ R }{2 \rho_w }\displaystyle\frac{ \Delta p }{ \Delta L }}$ |
Isso nos leva a obter:
| $ v_y = \displaystyle\frac{ u_{\tau} }{ \kappa }\ln\left(\displaystyle\frac{8 \rho_w u_{\tau} y }{ \eta }\right)$ |
onde se assume que $y_0 \sim 1/8.
ID:(14537, 0)
Espessura da camada de fluxo laminar
Equação
A espessura da camada laminar pode ser definida com base na condição de que os perfis de velocidade laminar coincidam com o perfil logarítmico correspondente ao fluxo turbulento. Isso ocorre quando
$y^+=u^+=\displaystyle\frac{1}{\kappa}\ln\left(\displaystyle\frac{y^+}{y_0}\right)$
cuja raiz é $7.072$. Uma vez que esta é uma estimativa de espessura, e a normalização inclui um fator de $1/8$, os números podem ser simplificados de primeira ordem, e a espessura pode ser estimada como:
| $ \delta = \displaystyle\frac{ \eta }{ \rho_w u_{\tau} }$ |
Na camada laminar, o fluxo tem a forma
$u^+ = y^+$
enquanto na região turbulenta é
$u^+=\displaystyle\frac{1}{\kappa}\ln\left(\displaystyle\frac{y^+}{y_0}\right)$
Igualando ambas as funções para definir a fronteira, obtemos a equação
$y^+=\displaystyle\frac{1}{\kappa}\ln\left(\displaystyle\frac{y^+}{y_0}\right)$
cuja solução numérica é
$y^+=7.072 \text{ e } y_0=\displaystyle\frac{7.072}{8}\sim 1$
onde foi usado o valor empírico para $y_0=1/8" e, dado que isso é uma estimativa, assumimos que $7/8\sim 1$.
Com a definição de normalização
$y^+=\displaystyle\frac{\rho_w u_{\tau}}{\eta} y = 1$
e resolvendo para $y$, obtemos
| $ \delta = \displaystyle\frac{ \eta }{ \rho_w u_{\tau} }$ |
ID:(14539, 0)
Tensão de cisalhamento nas paredes
Equação
A velocidade de corte, $u_{\tau}$, está diretamente associada à tensão de cisalhamento, $\tau_w$, gerada pelo fluxo nas paredes do tubo:
| $ \tau_w = \rho u_{\tau} ^2$ |
Isso exerce forças nas paredes e afeta sistemas que podem se mover, de forma semelhante ao caso em que o ar flui sobre a água.
ID:(14540, 0)