Turbulente Strömung durch Rohre
Storyboard 
Wenn die Reynoldszahl über 2000 liegt, wird der Fluss in einem Rohr immer instabil und wird schließlich vollständig turbulent. Infolgedessen ist es nicht mehr möglich, die Viskositätsannahme für laminare Strömung zu verwenden, die zur Hagen-Poiseuille-Gesetz führt, und ein alternatives Modell ist erforderlich.
Das Modell, das einen Fluss beschreibt, bei dem die Viskosität irrelevant ist, ist dasjenige, das zur Bernoulli-Gleichung führt. Dieses Modell geht jedoch davon aus, dass die Energiedichte erhalten bleibt. Eine Alternative besteht darin anzunehmen, dass Turbulenzen zu einer Durchmischung führen, bei der die Energiedichte nicht erhalten bleibt, sondern konstant bleibt. In diesem Fall kann der Fluss mit einer Gleichung modelliert werden, die der Bernoulli-Gleichung ähnelt, jedoch eine Korrektur zur Berücksichtigung der Homogenisierung aufgrund von Mischungseffekten enthält.
ID:(1970, 0)
Strömung an der laminaren Grenze
Notiz 
Wenn wir den Darcy-Weisbach Reibungsfaktor im laminaren Grenzbereich, wie durch
| $ f_D = \displaystyle\frac{64}{ Re }$ |
gegeben, in die Darcy-Weisbach-Gleichung einsetzen, die wie folgt ausgedrückt wird:
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
und die Definition der Reynolds-Zahl $Re$ verwenden, können wir zeigen, dass der Fluss durch
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
geregelt wird, was der Hagen-Poiseuille-Gleichung entspricht.
ID:(14530, 0)
Turbulente Strömung durch Rohre
Beschreibung 
Wenn die Reynoldszahl über 2000 liegt, wird der Fluss in einem Rohr immer instabil und wird schließlich vollständig turbulent. Infolgedessen ist es nicht mehr möglich, die Viskositätsannahme für laminare Strömung zu verwenden, die zur Hagen-Poiseuille-Gesetz führt, und ein alternatives Modell ist erforderlich. Das Modell, das einen Fluss beschreibt, bei dem die Viskosität irrelevant ist, ist dasjenige, das zur Bernoulli-Gleichung führt. Dieses Modell geht jedoch davon aus, dass die Energiedichte erhalten bleibt. Eine Alternative besteht darin anzunehmen, dass Turbulenzen zu einer Durchmischung führen, bei der die Energiedichte nicht erhalten bleibt, sondern konstant bleibt. In diesem Fall kann der Fluss mit einer Gleichung modelliert werden, die der Bernoulli-Gleichung ähnelt, jedoch eine Korrektur zur Berücksichtigung der Homogenisierung aufgrund von Mischungseffekten enthält.
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn zwischen zwei Punkten die Druckunterschied ($\Delta p$) existiert, wie durch die Gleichung bestimmt:
| $ dp = p - p_0 $ |
k nnen wir die Druck der Wassersäule ($p$) verwenden, definiert als:
| $ p_t = p_0 + \rho_w g h $ |
Dies ergibt:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Da die Höhendifferenz ($\Delta h$) wie folgt definiert ist:
| $ \Delta h = h_2 - h_1 $ |
kann die Druckunterschied ($\Delta p$) wie folgt ausgedr ckt werden:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedr ckt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfl che die Rohr Sektion ($S$) mit dem zur ckgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zur ckgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
(ID 4349)
Die urspr ngliche L sung von S.E. Haaland lautet wie folgt:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/R_H}{12}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Sie kann umgestellt werden, um den Ausdruck f r den Darcy-Weisbach-Reibungsfaktor $f_D$ wie folgt zu erhalten:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14534)
Die urspr ngliche L sung von S.E. Haaland lautet wie folgt:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/D_H}{3.7}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Sie kann umgestellt werden, um den Ausdruck f r den Darcy-Weisbach-Reibungsfaktor $f_D$ wie folgt zu erhalten:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14535)
Die Abschnitt oder Bereich ($S$) des Rohrs, das die Fl ssigkeit enth lt, kann als Funktion von die Tiefe in einer ungefüllten Tube ($h$) durch Integration ber den Radius bis der Rohrradius ($R$) ausgedr ckt werden:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Wenn wir diesen Ausdruck in Bezug auf den Faktor $h/R$ im Grenzwert $h\ll R$ entwickeln, erhalten wir im ersten Grad:
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
Wenn wir dies nach der Tiefe aufl sen, erhalten wir schlie lich:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 14541)
Da der Winkel zwischen dem Radius am Rand der Fl ssigkeitsoberfl che und der Vertikalen mit die Tiefe in einer ungefüllten Tube ($h$) und der Rohrradius ($R$) berechnet werden kann, gilt:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
Der entsprechende Bogen ist $R\phi$, also betr gt der gesamte Bogen:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
Analog dazu kann die halbe Oberfl che mit dem Satz des Pythagoras bestimmt werden, was zu folgendem Ergebnis f hrt:
$\sqrt{2Rh - h^2}$
Daher l sst sich der Hydrodynamischer Umfang ($P_H$) wie folgt ausdr cken:
$P_H = 2\sqrt{2Rh - h^2}+2R\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
Im Grenzfall einer kleinen H he, wo $h\ll R$, kann diese Gleichung entwickelt werden und f hrt zu:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 14542)
Beispiele
Wenn der Fluss in einem Rohr modelliert wird und angenommen wird, dass die Energiedichte erhalten bleibt, erh lt man die Bernoulli-Gleichung. Diese beschreibt den Fluss unter Verwendung von die Druckunterschied ($\Delta p$) in Abh ngigkeit von die Flüssigkeitsdichte ($\rho_w$), die Mittlere Geschwindigkeit der Flüssigkeit ($v$) und die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$):
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Im Fall von turbulenter Str mung wirkt der Mischprozess wie eine Reibung, die den Geschwindigkeitsgradienten, der im laminaren Fluss zwischen der Mitte und den Rohrw nden vorhanden ist, verringert. Wenn wir annehmen, dass dieser Mischprozess durch einen einfachen Korrekturfaktor modelliert werden kann, gelangen wir empirisch zur Darcy-Weisbach-Gleichung, die der Darcy-Weisbach-Reibungsfaktor ($f_D$), der Rohrlänge ($\Delta L$) und die Hydrodynamischer Durchmesser ($D_H$) einbezieht:
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
Der Faktor der Darcy-Weisbach-Reibungsfaktor ($f_D$) wurde empirisch f r verschiedene Str mungsbedingungen bestimmt und wird in Abh ngigkeit von der Anzahl der Reynold ($Re$) ausgedr ckt.
(ID 15893)
Im Jahr 1944 ma Lewis Ferry Moody den Darcy-Weisbach Reibungsfaktor als Funktion der Reynolds-Zahl und der relativen Rauheit der Wand, was zur Erstellung des folgenden Diagramms f hrte:
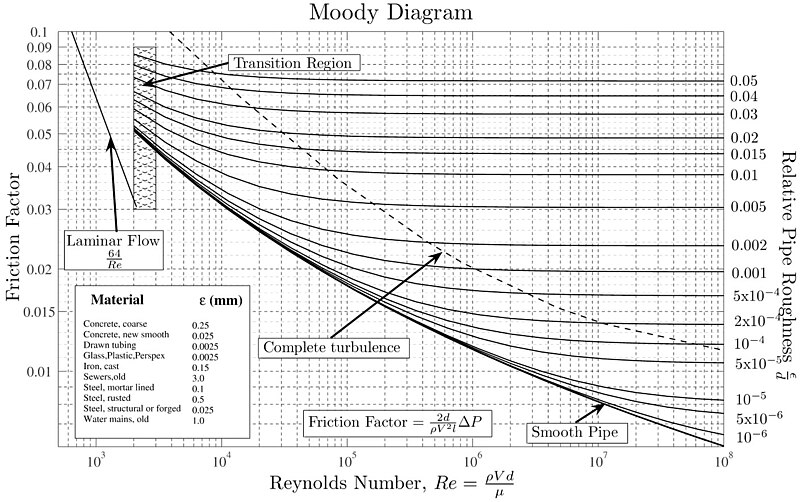
Die relative Rauheit kann gesch tzt werden, indem die Gr e der Oberfl chenrauheit (H he der Vorspr nge oder Tiefe der Vertiefungen) im Verh ltnis zum hydraulischen Durchmesser ber cksichtigt wird.
Es sind zwei unterschiedliche Verhaltensweisen zu beobachten:
• F r Reynolds-Zahlen unter 2000 h ngt der Darcy-Weisbach Reibungsfaktor nur von der Reynolds-Zahl ab und folgt einer Beziehung von $64/Re$. Dies entspricht dem laminaren Str mungsregime.
• F r Reynolds-Zahlen ber 2000 wird ein Verhalten beobachtet, das sowohl von der Reynolds-Zahl als auch von der relativen Rauheit der Oberfl che des Rohrs abh ngt.
(ID 14528)
Im Zusammenhang mit der Darcy-Weisbach-Gleichung wird eine Hydrodynamischer Durchmesser ($D_H$) verwendet, was einer Verallgemeinerung des traditionellen Durchmessers eines Kreises entspricht. Dies erm glicht es, einen nicht kreisf rmigen Querschnitt zu betrachten und einen quivalenten Durchmesser basierend auf der Fl che von die Rohr Sektion ($S$) und der Umfang ($P$) mit der folgenden Formel zu berechnen:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
F r einen kreisf rmigen Querschnitt erhalten wir den traditionellen Durchmesser eines Kreises wie folgt:
$D_H = \displaystyle\frac{4 S}{P} = \displaystyle\frac{4 \pi R^2}{2 \pi R} = 2R$
(ID 15894)
Im Zusammenhang mit dem Darcy-Weisbach-Reibungsfaktor wird ein Hydraulischer Radius ($R_H$) verwendet, was eine Verallgemeinerung des traditionellen Radius eines Kreises darstellt. Auf diese Weise ist es m glich, einen Durchmesser basierend auf der Fl che von die Rohr Sektion ($S$) und dem Umfang im Kontakt mit der Hydrodynamischer Umfang ($P_H$) mithilfe der folgenden Formel zu berechnen:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
F r einen kreisf rmigen Querschnitt k nnen wir den traditionellen hydraulischen Radius eines Kreises wie folgt berechnen:
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
(ID 15895)
In einem zylindrischen Rohr ist die Tiefe wie folgt mit dem Durchfluss verbunden:

Durch die Integration von die Abschnitt oder Bereich ($S$) k nnen wir berechnen, wie sich die Fl che in Abh ngigkeit von die Tiefe in einer ungefüllten Tube ($h$) ber das Integral bis zum Radius der Rohrradius ($R$) ndert, was ergibt:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Bei kleinen Durchfl ssen, bei denen die Tiefe deutlich geringer ist als der Radius, vereinfacht sich die Beziehung zwischen Querschnittsfl che und Tiefe erheblich. Durch L sen der Gleichung f r die Tiefe erhalten wir:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 15896)
Der Hydrodynamischer Umfang ($P_H$) in einem teilweise gef llten Rohr entspricht den R ndern des Querschnitts, die mit der Fl ssigkeit in Kontakt stehen, also dem Bogen, der sowohl die Rohrwand als auch die Oberfl che ber hrt:

Dementsprechend kann es allgemein als Funktion von der Rohrradius ($R$) und die Tiefe in einer ungefüllten Tube ($h$) ausgedr ckt werden:
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
F r kleine Durchfl sse, bei denen die Tiefe deutlich kleiner als der Radius ist, vereinfacht sich diese Beziehung zwischen dem Querschnitt und der Tiefe zu:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 15897)
Wenn wir den Darcy-Weisbach Reibungsfaktor im laminaren Grenzbereich, wie durch
| $ f_D = \displaystyle\frac{64}{ Re }$ |
gegeben, in die Darcy-Weisbach-Gleichung einsetzen, die wie folgt ausgedr ckt wird:
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
und die Definition der Reynolds-Zahl $Re$ verwenden, k nnen wir zeigen, dass der Fluss durch
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
geregelt wird, was der Hagen-Poiseuille-Gleichung entspricht.
(ID 14530)
ID:(1970, 0)
