Utilizador:
Fluxo turbulento através de tubos abertos
Storyboard 
Para números de Reynolds elevados, o fluxo em uma tubulação torna-se turbulento, provocando uma perda significativa de energia que deve ser considerada em qualquer modelagem do sistema.
No caso de uma tubulação aberta, o atrito do fluido é descrito pela equação de Darcy-Weisbach para a queda de pressão, ou sua altura equivalente. Essa perda de energia é modelada usando um fator de fricção específico, que varia conforme as características do fluxo e as condições da tubulação.
ID:(2110, 0)
Equação de Darcy-Weisbach
Conceito
Ao modelar o fluxo em um tubo, assumindo que a densidade de energia é conservada, obtém-se a equação de Bernoulli. Esta equação descreve o fluxo utilizando la diferença de pressão ($\Delta p$) em termos de la densidade líquida ($\rho_w$), la velocidade média do fluido ($v$) e la diferença de velocidade entre superfícies ($\Delta v$):
| $ \Delta p = - \rho \bar{v} \Delta v $ |
No caso de fluxo turbulento, o processo de mistura atua como uma fricção que reduz o gradiente de velocidade presente no fluxo laminar entre o centro e as paredes do tubo. Se assumirmos que este efeito de mistura pode ser modelado com um simples fator de correção, chegamos empiricamente à equação de Darcy-Weisbach, que envolve o fator de atrito Darcy-Weisbach ($f_D$), o comprimento do tubo ($\Delta L$) e la diâmetro hidrodinâmico ($D_H$):
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
O fator o fator de atrito Darcy-Weisbach ($f_D$) foi determinado empiricamente para várias condições de fluxo e é expresso em função de o número de Reynolds ($Re$).
ID:(15893, 0)
Diagrama Moody
Imagem
Em 1944, Lewis Ferry Moody mediu o fator de atrito de Darcy-Weisbach como função do número de Reynolds e da rugosidade relativa da parede, resultando na criação do seguinte diagrama:
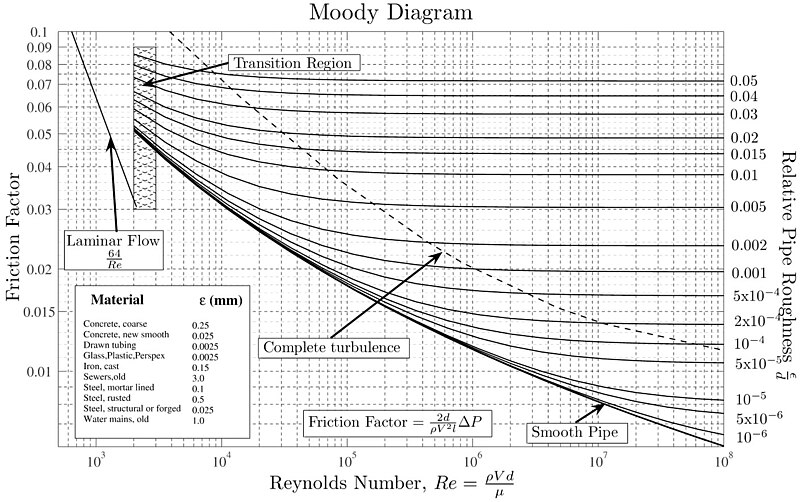
A rugosidade relativa pode ser estimada considerando o tamanho das irregularidades da superfície (altura de saliências ou profundidade de sulcos) em relação ao diâmetro hidráulico.
São observados dois comportamentos distintos:
• Para números de Reynolds abaixo de 2000, o fator de atrito de Darcy-Weisbach depende apenas do número de Reynolds, seguindo uma relação de $64/Re$. Isso corresponde ao regime de escoamento laminar.
• Para números de Reynolds acima de 2000, observa-se um comportamento que depende tanto do número de Reynolds quanto da rugosidade relativa da superfície do tubo.
ID:(14528, 0)
Diâmetro hidráulico
Conceito
No contexto da equação de Darcy-Weisbach, utiliza-se uma diâmetro hidrodinâmico ($D_H$), que corresponde a uma generalização do diâmetro tradicional de um círculo. Isso permite considerar uma seção que não seja circular e calcular um diâmetro equivalente com base na área de la seção de tubo ($S$) e seu o perímetro ($P$) utilizando a seguinte fórmula:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
Para uma seção circular, obtemos o diâmetro tradicional de um círculo da seguinte maneira:
$D_H = \displaystyle\frac{4 S}{P} = \displaystyle\frac{4 \pi R^2}{2 \pi R} = 2R$
ID:(15894, 0)
Perímetro hidrodinâmico em tubo não preenchido
Conceito
O perímetro hidrodinâmico ($P_H$) em um tubo parcialmente cheio corresponde às bordas da seção que estão em contato com o líquido, ou seja, o arco que toca tanto a parede do tubo quanto a superfície:
Assim, podemos expressá-lo geralmente em função de o raio do tubo ($R$) e la profundidade em um tubo vazio ($h$) da seguinte forma:
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
Para fluxos pequenos, onde a profundidade é significativamente menor que o raio, isso simplifica a relação entre a área da seção transversal e a profundidade para:
| $ P_H = \sqrt{2^5 R h }$ |
ID:(15897, 0)
Profundidade de um tubo vazio
Conceito
Em um tubo cilíndrico, a profundidade está relacionada com o fluxo da seguinte maneira:
Ao integrar la seção ou superfície ($S$), podemos calcular como a superfície varia em função de la profundidade em um tubo vazio ($h$) por meio da integral sobre o raio até O raio do tubo ($R$), o que resulta em:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Para fluxos pequenos, onde a profundidade é significativamente menor que o raio, a relação entre a seção transversal e a profundidade se simplifica consideravelmente. Ao resolver a equação de profundidade, obtemos:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
ID:(15896, 0)
Raio hidráulico
Conceito
No contexto do fator de fricção de Darcy-Weisbach, utiliza-se um raio hidráulico ($R_H$), que é uma generalização do raio tradicional de um círculo. Dessa forma, é possível calcular um diâmetro com base na área de la seção de tubo ($S$) e seu perímetro em contato com o perímetro hidrodinâmico ($P_H$), utilizando a seguinte fórmula:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
Para uma seção circular, podemos obter o raio hidráulico tradicional de um círculo da seguinte maneira:
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
ID:(15895, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \Delta h_d = \displaystyle\frac{ \Delta L }{ 2 g D_H } f_D j_s ^2 $
Dh_d = DL * f_D * j_s ^2/(2* g * D_H )
$ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $
Dp = DL * f_D * rho_w * j_s ^2/(2* D_H )
$ D_H = \displaystyle\frac{ 4 S }{ P }$
D_H = 4 * S / P
$ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$
f_D = 25/(81*(log(( e /(12* R_H ))^1.11 + 6.9/ Re ))^2)
$ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$
h = (3^2* S ^2/(2^3* R ))^(1/3)
$ j_s = \displaystyle\frac{ J_V }{ S }$
j_s = J_V / S
$ P_H = \sqrt{2^5 R h }$
P_H = sqrt(2^5* R * h )
$ Re =\displaystyle\frac{ \rho_w R j_s }{ \eta }$
Re = rho * R * v / eta
$ R_H = \displaystyle\frac{ S }{ P_H }$
R_H = S / P_H
$ S = \pi R ^2$
S = pi * r ^2
ID:(15883, 0)
Superfície de um disco
Equação
La superfície de um disco ($S$) de um raio do disco ($r$) é calculada da seguinte forma:
| $ S = \pi R ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 0)
Fluxo de volume e sua velocidade
Equação
Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) através da seguinte fórmula:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
O fluxo é definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equação:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
e o volume é igual à área da seção la seção de tubo ($S$) multiplicada pela distância percorrida o elemento de tubo ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Como a distância percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde à velocidade, ela é representada por:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Assim, o fluxo é Uma densidade de fluxo ($j_s$), que é calculado usando:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 0)
Número de Reynolds
Equação
O critério chave para determinar se um meio é laminar ou turbulento é o chamado número de Reynolds, que compara a energia associada à inércia com aquela associada à viscosidade. A primeira depende de la densidade ($\rho$), la velocidade média do fluido ($v$) e la dimensão típica do sistema ($R$), enquanto a segunda depende de la viscosidade ($\eta$), definindo-o como:
| $ Re =\displaystyle\frac{ \rho_w R j_s }{ \eta }$ |
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Profundidade de um tubo vazio
Equação
La profundidade em um tubo vazio ($h$) pode ser estimado quando o nível do líquido é baixo, ou seja, quando esse nível é muito menor que o raio do tubo, em função de la seção ou superfície ($S$) e o raio do tubo ($R$):
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
La seção ou superfície ($S$) do tubo que contém o líquido pode ser expressa como uma função de la profundidade em um tubo vazio ($h$) integrando sobre o raio até O raio do tubo ($R$):
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Se expandirmos essa expressão em termos do fator $h/R$ no limite $h\ll R$, obtemos, em primeira ordem:
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
Se resolvermos para a profundidade, obtemos finalmente:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
ID:(14541, 0)
Perímetro hidrodinâmico em tubo não preenchido
Equação
O perímetro hidrodinâmico ($P_H$) pode ser estimado a partir de la profundidade em um tubo vazio ($h$) e o raio do tubo ($R$) utilizando:
| $ P_H = \sqrt{2^5 R h }$ |
Como o ângulo entre o raio na borda da superfície do líquido e a vertical pode ser calculado usando la profundidade em um tubo vazio ($h$) e o raio do tubo ($R$) por meio de:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
O arco correspondente é $R\phi$, portanto, o arco total é:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
De maneira análoga, metade da área pode ser determinada utilizando o teorema de Pitágoras, resultando em:
$\sqrt{2Rh - h^2}$
Portanto, o perímetro hidrodinâmico ($P_H$) é expresso como:
$P_H = 2\sqrt{2Rh - h^2}+2R\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
No limite de uma pequena altura, onde $h\ll R$, essa expressão pode ser expandida, resultando em:
| $ P_H = \sqrt{2^5 R h }$ |
ID:(14542, 0)
Raio hidráulico
Equação
O raio hidráulico ($R_H$) pode ser calculado usando la seção de tubo ($S$) e o perímetro hidrodinâmico ($P_H$) por meio de:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
ID:(14531, 0)
Diâmetro hidráulico
Equação
La diâmetro hidrodinâmico ($D_H$) pode ser calculado a partir de la seção de tubo ($S$) e o perímetro ($P$) por meio de:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
ID:(14527, 0)
Solução para tubo aberto
Equação
A equação de Colebrook-White para o caso de um tubo fechado:
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{12 R_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
é uma equação implícita utilizada para determinar o fator de atrito de Darcy-Weisbach ($f_D$). Para resolver esta equação, foram desenvolvidas várias aproximações que variam em complexidade e precisão. Uma das aproximações mais eficazes, que abrange uma ampla faixa de números de Reynolds $Re$, é a proposta por S.E. Haaland:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
A solução original de S.E. Haaland é a seguinte:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/R_H}{12}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Pode ser rearranjada para obter a expressão do fator de atrito de Darcy-Weisbach $f_D$ da seguinte forma:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
ID:(14534, 0)
Equação de Darcy-Weisbach
Equação
A equação de Darcy-Weisbach permite calcular la diferença de pressão ($\Delta p$) em função de la densidade líquida ($\rho_w$), la diâmetro hidrodinâmico ($D_H$), o fator de atrito Darcy-Weisbach ($f_D$), o comprimento do tubo ($\Delta L$) e la velocidade média do fluido ($v$) através de:
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
ID:(14526, 0)
Perda de energia devido à turbulência e fricção
Equação
A equação de Darcy-Weisbach permite calcular la diferença de pressão ($\Delta p$) em função de la densidade líquida ($\rho_w$), la diâmetro hidrodinâmico ($D_H$), o fator de atrito Darcy-Weisbach ($f_D$), o comprimento do tubo ($\Delta L$) e la velocidade média do fluido ($v$) através de:
| $ \Delta h_d = \displaystyle\frac{ \Delta L }{ 2 g D_H } f_D j_s ^2 $ |
ID:(15958, 0)