Utilizador:
Diferença de pressão
Storyboard 
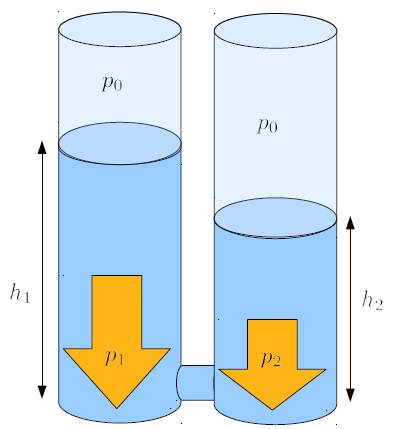
Quando duas colunas de líquido com alturas diferentes são conectadas, pode-se gerar uma diferença de pressão que leva ao deslocamento do líquido da coluna mais alta para a coluna de menor altura. Esse movimento continua até que ambas as colunas atinjam a mesma altura, eliminando qualquer diferença de pressão.
ID:(1608, 0)
Conectando duas colunas de líquido
Conceito
Ao conectar duas colunas de água com alturas diferentes em suas bases, é criada uma situação em que existe uma diferença de pressão ao longo do tubo conectado.
Esse arranjo nos permite estudar como a diferença de pressão gera um fluxo de líquido ao longo do tubo. Podemos pensar em um elemento de líquido com determinado comprimento e seção transversal igual à do tubo, e estimar a massa correspondente usando a densidade. Com a seção transversal, também podemos converter a diferença de pressão em uma diferença de forças e, assim, estudar como os volumes de líquidos são acelerados devido às diferenças de pressão.
ID:(933, 0)
Diferença de pressão entre colunas
Conceito
Se houver la diferença de pressão ($\Delta p$) entre dois pontos, conforme determinado pela equação:
| $ \Delta p = p_2 - p_1 $ |
podemos usar la pressão da coluna de água ($p$), que é definida como:
| $ p_t = p_0 + \rho_w g h $ |
Isso resulta em:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Como la diferença de altura ($\Delta h$) é:
| $ \Delta h = h_2 - h_1 $ |
la diferença de pressão ($\Delta p$) pode ser expressa como:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(15704, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \Delta h = h_2 - h_1 $
Dh = h_2 - h_1
$ \Delta p = p_2 - p_1 $
Dp = p_2 - p_1
$ \Delta p = \rho_w g \Delta h $
Dp = rho_w * g * Dh
$ p_1 = \rho_w g h_1 $
p = rho_w * g * h
$ p_2 = \rho_w g h_2 $
p = rho_w * g * h
ID:(15479, 0)
Diferença de altura
Equação
Quando duas colunas de líquido são conectadas com la altura da coluna líquida 1 ($h_1$) e la altura da coluna líquida 2 ($h_2$), é criada uma la diferença de altura ($\Delta h$), que é calculada da seguinte forma:
| $ \Delta h = h_2 - h_1 $ |
A La diferença de altura ($\Delta h$) irá gerar a diferença de pressão que fará o líquido fluir da coluna mais alta para a coluna mais baixa.
ID:(4251, 0)
Diferença de pressão
Equação
Quando duas colunas de líquido são conectadas com la pressão na coluna 1 ($p_1$) e la pressão na coluna 2 ($p_2$), é criada uma la diferença de pressão ($\Delta p$) que é calculada de acordo com a seguinte fórmula:
| $ \Delta p = p_2 - p_1 $ |
la diferença de pressão ($\Delta p$) representa a diferença de pressão que fará o líquido fluir da coluna mais alta para a coluna mais baixa.
ID:(4252, 0)
Pressão da coluna (1)
Equação
Se considerarmos a expressão de la força da coluna ($F$) e a dividirmos por la altura da coluna líquida ($S$), obtemos la pressão da coluna de água ($p$). Nesse processo, simplificamos la altura da coluna líquida ($S$), de modo que não dependa mais dele. A expressão resultante é a seguinte:
| $ p_1 = \rho_w g h_1 $ |
| $ p = \rho_w g h $ |
Como a la força da coluna ($F$) gerada por uma coluna de líquido de la altura da coluna ($h$), la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$) é
| $ F = S h \rho_w g $ |
e a la pressão da coluna de água ($p$) é definida então como
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
temos que a la pressão da coluna de água ($p$) gerada por uma coluna de líquido é
| $ p = \rho_w g h $ |
ID:(4249, 1)
Pressão da coluna (2)
Equação
Se considerarmos a expressão de la força da coluna ($F$) e a dividirmos por la altura da coluna líquida ($S$), obtemos la pressão da coluna de água ($p$). Nesse processo, simplificamos la altura da coluna líquida ($S$), de modo que não dependa mais dele. A expressão resultante é a seguinte:
| $ p_2 = \rho_w g h_2 $ |
| $ p = \rho_w g h $ |
Como a la força da coluna ($F$) gerada por uma coluna de líquido de la altura da coluna ($h$), la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$) é
| $ F = S h \rho_w g $ |
e a la pressão da coluna de água ($p$) é definida então como
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
temos que a la pressão da coluna de água ($p$) gerada por uma coluna de líquido é
| $ p = \rho_w g h $ |
ID:(4249, 2)
Diferença de pressão entre colunas
Equação
A diferença de altura, representada por la diferença de altura ($\Delta h$), implica que a pressão em ambas as colunas é diferente. Em particular, la diferença de pressão ($\Delta p$) é uma função de la densidade líquida ($\rho_w$), la aceleração gravitacional ($g$) e la diferença de altura ($\Delta h$), da seguinte forma:
| $ \Delta p = \rho_w g \Delta h $ |
Se houver la diferença de pressão ($\Delta p$) entre dois pontos, conforme determinado pela equação:
| $ \Delta p = p_2 - p_1 $ |
podemos usar la pressão da coluna de água ($p$), que é definida como:
| $ p_t = p_0 + \rho_w g h $ |
Isso resulta em:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Como la diferença de altura ($\Delta h$) é:
| $ \Delta h = h_2 - h_1 $ |
la diferença de pressão ($\Delta p$) pode ser expressa como:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)