Usuario:
Diferencia de Presión
Storyboard 
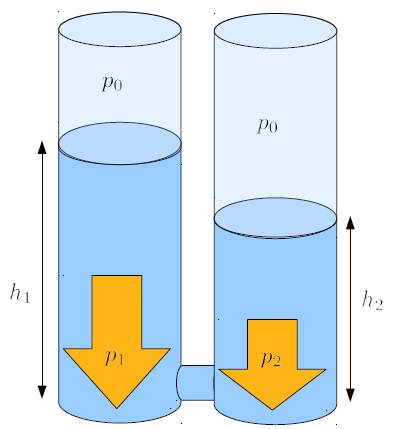
Cuando se conectan dos columnas de líquido con alturas diferentes, se puede crear una disparidad de presión que resulta en un desplazamiento del líquido desde la columna más alta hacia la columna de menor altura. Este movimiento persiste hasta que ambas columnas alcanzan la misma altura, eliminando así cualquier diferencia de presión.
ID:(1608, 0)
Diferencia de Presión
Storyboard
Cuando se conectan dos columnas de líquido con alturas diferentes, se puede crear una disparidad de presión que resulta en un desplazamiento del líquido desde la columna más alta hacia la columna de menor altura. Este movimiento persiste hasta que ambas columnas alcanzan la misma altura, eliminando así cualquier diferencia de presión.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Como la la fuerza de la columna ($F$) generada por una columna de liquido de la altura de la columna ($h$), la sección de la columna ($S$), la densidad del líquido ($\rho_w$) y la aceleración gravitacional ($g$) es
y la la presión de la columna de agua ($p$) se define entonces como
se tiene que la la presión de la columna de agua ($p$) generada por una columna de liquido es
Como la la fuerza de la columna ($F$) generada por una columna de liquido de la altura de la columna ($h$), la sección de la columna ($S$), la densidad del líquido ($\rho_w$) y la aceleración gravitacional ($g$) es
y la la presión de la columna de agua ($p$) se define entonces como
se tiene que la la presión de la columna de agua ($p$) generada por una columna de liquido es
Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:
podemos usar la presión de la columna de agua ($p$), que es:
Esto nos da:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Dado que la diferencia de altura ($\Delta h$) es:
la diferencia de presión ($\Delta p$) se puede expresar como:
Ejemplos
Si se conectan dos columnas de agua de alturas diferentes en sus bases, se genera una situaci n en la que existe una diferencia de presi n a lo largo del tubo conectado.
Este montaje nos permite estudiar c mo la diferencia de presi n genera un flujo de l quido a lo largo del tubo. Podemos pensar en un elemento de l quido de cierta longitud con una secci n igual a la secci n del tubo, y mediante la densidad estimar la masa correspondiente. Con la secci n tambi n podemos convertir la diferencia de presi n en una diferencia de fuerzas, y as estudiar la forma en que los vol menes de los l quidos son acelerados debido a las diferencias de presi n.
Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:
podemos usar la presión de la columna de agua ($p$), que es:
Esto nos da:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Dado que la diferencia de altura ($\Delta h$) es:
la diferencia de presión ($\Delta p$) se puede expresar como:
Cuando se conectan dos columnas de l quido con la altura de columna de líquido 1 ($h_1$) y la altura de columna de líquido 2 ($h_2$), se crea una la diferencia de altura ($\Delta h$) que se calcula de acuerdo con la siguiente f rmula:
la diferencia de altura ($\Delta h$) generar la diferencia de presiones que desplazar el l quido de la columna m s alta hacia la columna m s baja.
Cuando se conectan dos columnas de l quido con la presión en la columna 1 ($p_1$) y la presión en la columna 2 ($p_2$), se crea una la diferencia de presión ($\Delta p$) que se calcula mediante la siguiente f rmula:
la diferencia de presión ($\Delta p$) representa la diferencia de presiones que desplazar el l quido de la columna m s alta hacia la columna m s baja.
Si consideramos la expresi n de la fuerza de la columna ($F$) y la dividimos por la sección de la columna ($S$), obtenemos la presión de la columna de agua ($p$). Durante este proceso, simplificamos la sección de la columna ($S$), por lo que ya no depende de esta. La expresi n resultante es la siguiente:
Si consideramos la expresi n de la fuerza de la columna ($F$) y la dividimos por la sección de la columna ($S$), obtenemos la presión de la columna de agua ($p$). Durante este proceso, simplificamos la sección de la columna ($S$), por lo que ya no depende de esta. La expresi n resultante es la siguiente:
La diferencia de alturas, representada por la diferencia de altura ($\Delta h$), implica que la presi n en ambas columnas es diferente. En particular, la diferencia de presión ($\Delta p$) es una funci n de la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$) y la diferencia de altura ($\Delta h$), de la siguiente manera:
ID:(1608, 0)
