User:
Pressure difference
Storyboard 
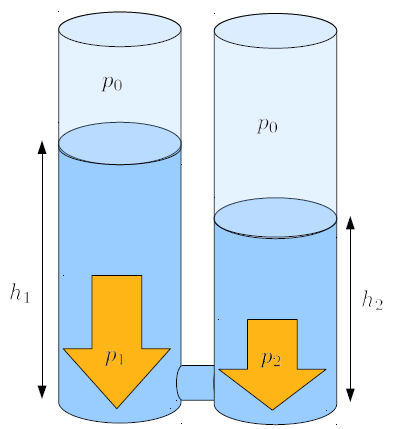
When two columns of liquid with different heights are connected, it can generate a pressure difference that leads to a flow of liquid from the taller column to the shorter one. This movement continues until both columns reach the same height, eliminating any pressure difference.
ID:(1608, 0)
Connecting two liquid columns
Concept
If two columns of water with different heights at their bases are connected, a situation arises where there is a pressure difference along the connecting tube.
This setup allows us to study how the pressure difference generates a liquid flow along the tube. We can consider an element of liquid with a certain length and a section equal to that of the tube, and estimate the corresponding mass using the density. With the section, we can also convert the pressure difference into a force difference and, ultimately, study how volumes in liquids are accelerated due to pressure differences.
ID:(933, 0)
Pressure difference between columns
Concept
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
| $ \Delta p = p_2 - p_1 $ |
we can utilize the water column pressure ($p$), which is defined as:
| $ p_t = p_0 + \rho_w g h $ |
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
| $ \Delta h = h_2 - h_1 $ |
the pressure difference ($\Delta p$) can be expressed as:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(15704, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta h = h_2 - h_1 $
Dh = h_2 - h_1
$ \Delta p = p_2 - p_1 $
Dp = p_2 - p_1
$ \Delta p = \rho_w g \Delta h $
Dp = rho_w * g * Dh
$ p_1 = \rho_w g h_1 $
p = rho_w * g * h
$ p_2 = \rho_w g h_2 $
p = rho_w * g * h
ID:(15479, 0)
Height difference
Equation
When two liquid columns are connected with the height of liquid column 1 ($h_1$) and the height of liquid column 2 ($h_2$), a the height difference ($\Delta h$) is formed, which is calculated as follows:
| $ \Delta h = h_2 - h_1 $ |
the height difference ($\Delta h$) will generate the pressure difference that will cause the liquid to flow from the higher column to the lower one.
ID:(4251, 0)
Pressure difference
Equation
When two liquid columns are connected with the pressure in column 1 ($p_1$) and the pressure in column 2 ($p_2$), a the pressure difference ($\Delta p$) is formed, which is calculated according to the following formula:
| $ \Delta p = p_2 - p_1 $ |
the pressure difference ($\Delta p$) represents the pressure difference that will cause the liquid to flow from the taller column to the shorter one.
ID:(4252, 0)
Pressure of a column (1)
Equation
If we consider the expression of the column force ($F$) and divide it by the column Section ($S$), we obtain the water column pressure ($p$). In this process, we simplify the column Section ($S$), so it no longer depends on it. The resulting expression is:
| $ p_1 = \rho_w g h_1 $ |
| $ p = \rho_w g h $ |
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
| $ F = S h \rho_w g $ |
and the the water column pressure ($p$) is then defined as
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
we have that the the water column pressure ($p$) generated by a column of liquid is
| $ p = \rho_w g h $ |
ID:(4249, 1)
Pressure of a column (2)
Equation
If we consider the expression of the column force ($F$) and divide it by the column Section ($S$), we obtain the water column pressure ($p$). In this process, we simplify the column Section ($S$), so it no longer depends on it. The resulting expression is:
| $ p_2 = \rho_w g h_2 $ |
| $ p = \rho_w g h $ |
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
| $ F = S h \rho_w g $ |
and the the water column pressure ($p$) is then defined as
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
we have that the the water column pressure ($p$) generated by a column of liquid is
| $ p = \rho_w g h $ |
ID:(4249, 2)
Pressure difference between columns
Equation
The height difference, denoted by the height difference ($\Delta h$), implies that the pressure in both columns is distinct. In particular, the pressure difference ($\Delta p$) is a function of the liquid density ($\rho_w$), the gravitational Acceleration ($g$), and the height difference ($\Delta h$), as follows:
| $ \Delta p = \rho_w g \Delta h $ |
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
| $ \Delta p = p_2 - p_1 $ |
we can utilize the water column pressure ($p$), which is defined as:
| $ p_t = p_0 + \rho_w g h $ |
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
| $ \Delta h = h_2 - h_1 $ |
the pressure difference ($\Delta p$) can be expressed as:
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)