Utilisateur:
Différence de pression
Storyboard 
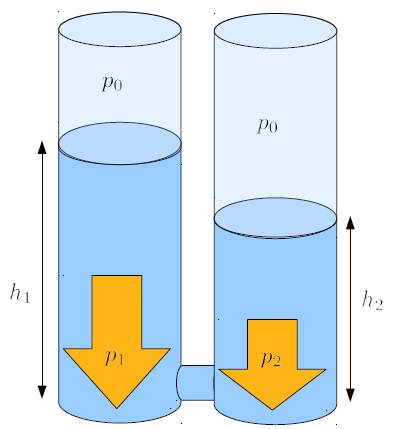
Lorsque deux colonnes de liquide de hauteurs différentes sont connectées, cela peut créer une différence de pression qui entraîne un déplacement du liquide de la colonne la plus haute vers celle de moindre hauteur. Ce mouvement se poursuit jusqu'à ce que les deux colonnes atteignent la même hauteur, éliminant ainsi toute différence de pression.
ID:(1608, 0)
Connexion de deux colonnes de liquide
Concept
En reliant deux colonnes d'eau de hauteurs différentes à leur base, on obtient une situation où il existe une différence de pression le long du tuyau connecteur.
Ce montage nous permet d'étudier comment la différence de pression génère un mouvement de liquide le long du tuyau. On peut considérer un élément de liquide d'une certaine longueur avec une section égale à celle du tuyau et, en utilisant la densité, estimer la masse correspondante. Avec la section, on peut également convertir la différence de pression en une différence de forces et ainsi étudier comment les volumes de liquides sont accélérés en raison des différences de pression.
ID:(933, 0)
Différence de pression entre les colonnes
Concept
S'il existe a différence de pression ($\Delta p$) entre deux points, comme le détermine l'équation :
| $ \Delta p = p_2 - p_1 $ |
nous pouvons utiliser a pression de la colonne d'eau ($p$), qui est définie comme suit :
| $ p_t = p_0 + \rho_w g h $ |
Cela donne :
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Comme a différence de hauteur ($\Delta h$) est définie comme suit :
| $ \Delta h = h_2 - h_1 $ |
a différence de pression ($\Delta p$) peut être exprimée comme suit :
| $ \Delta p = \rho_w g \Delta h $ |
ID:(15704, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta h = h_2 - h_1 $
Dh = h_2 - h_1
$ \Delta p = p_2 - p_1 $
Dp = p_2 - p_1
$ \Delta p = \rho_w g \Delta h $
Dp = rho_w * g * Dh
$ p_1 = \rho_w g h_1 $
p = rho_w * g * h
$ p_2 = \rho_w g h_2 $
p = rho_w * g * h
ID:(15479, 0)
Différence de hauteur
Équation
Lorsque deux colonnes de liquide sont connectées avec a hauteur de colonne de liquide 1 ($h_1$) et a hauteur de colonne de liquide 2 ($h_2$), une a différence de hauteur ($\Delta h$) est formée, qui est calculée comme suit :
| $ \Delta h = h_2 - h_1 $ |
a différence de hauteur ($\Delta h$) générera la différence de pression qui fera s'écouler le liquide de la colonne la plus élevée vers la colonne la plus basse.
ID:(4251, 0)
Différence de pression
Équation
Lorsque deux colonnes de liquide sont connectées avec a pression dans la colonne 1 ($p_1$) et a pression dans la colonne 2 ($p_2$), une a différence de pression ($\Delta p$) est créée, qui est calculée selon la formule suivante :
| $ \Delta p = p_2 - p_1 $ |
a différence de pression ($\Delta p$) représente la différence de pression qui fera s'écouler le liquide de la colonne la plus haute vers la colonne la plus basse.
ID:(4252, 0)
Pression de colonne (1)
Équation
Si l'on considère l'expression de a force de la colonne ($F$) et qu'on la divise par a hauteur de la colonne de liquide ($S$), on obtient a pression de la colonne d'eau ($p$). Au cours de ce processus, nous simplifions a hauteur de la colonne de liquide ($S$), de sorte qu'il ne dépende plus de lui. L'expression résultante est la suivante :
| $ p_1 = \rho_w g h_1 $ |
| $ p = \rho_w g h $ |
Comme la a force de la colonne ($F$) générée par une colonne de liquide de a hauteur de la colonne ($h$), a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) est
| $ F = S h \rho_w g $ |
et la a pression de la colonne d'eau ($p$) est alors définie comme
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
nous avons donc que la a pression de la colonne d'eau ($p$) générée par une colonne de liquide est
| $ p = \rho_w g h $ |
ID:(4249, 1)
Pression de colonne (2)
Équation
Si l'on considère l'expression de a force de la colonne ($F$) et qu'on la divise par a hauteur de la colonne de liquide ($S$), on obtient a pression de la colonne d'eau ($p$). Au cours de ce processus, nous simplifions a hauteur de la colonne de liquide ($S$), de sorte qu'il ne dépende plus de lui. L'expression résultante est la suivante :
| $ p_2 = \rho_w g h_2 $ |
| $ p = \rho_w g h $ |
Comme la a force de la colonne ($F$) générée par une colonne de liquide de a hauteur de la colonne ($h$), a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) est
| $ F = S h \rho_w g $ |
et la a pression de la colonne d'eau ($p$) est alors définie comme
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
nous avons donc que la a pression de la colonne d'eau ($p$) générée par une colonne de liquide est
| $ p = \rho_w g h $ |
ID:(4249, 2)
Différence de pression entre les colonnes
Équation
La différence de hauteur, représentée par a différence de hauteur ($\Delta h$), implique que la pression dans les deux colonnes est différente. En particulier, a différence de pression ($\Delta p$) est une fonction de a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), et a différence de hauteur ($\Delta h$), comme suit :
| $ \Delta p = \rho_w g \Delta h $ |
S'il existe a différence de pression ($\Delta p$) entre deux points, comme le détermine l'équation :
| $ \Delta p = p_2 - p_1 $ |
nous pouvons utiliser a pression de la colonne d'eau ($p$), qui est définie comme suit :
| $ p_t = p_0 + \rho_w g h $ |
Cela donne :
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Comme a différence de hauteur ($\Delta h$) est définie comme suit :
| $ \Delta h = h_2 - h_1 $ |
a différence de pression ($\Delta p$) peut être exprimée comme suit :
| $ \Delta p = \rho_w g \Delta h $ |
ID:(4345, 0)