Utilisateur:
Pression hydrostatique
Storyboard 
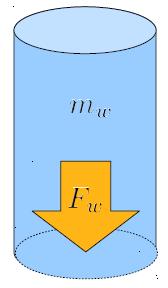
Une colonne de liquide exerce une force sur sa base en raison de sa masse. Étant donné que cette force est directement proportionnelle à la surface de section transversale, il est utile d'introduire le concept de force par unité de surface, que nous appelons pression.
La pression peut être influencée par le mouvement du liquide, et nous faisons la distinction entre la pression générale et la pression hydrostatique (hydro = liquide, statique = sans mouvement).
ID:(874, 0)
Mécanismes
Iframe
Mécanismes
ID:(15432, 0)
Description de la colonne d'eau
Concept
Pour étudier le comportement des liquides, il est utile d'introduire le concept de colonne de liquide. Cette colonne est une abstraction d'un contenant cylindrique (comme une éprouvette graduée) contenant du liquide, et permet d'étudier la force à laquelle un objet à l'intérieur est exposé.
Une fois ce concept introduit, nous pouvons penser à son existence indépendamment du contenant qui le contient. Par exemple, un plongeur nageant en haute mer est exposé au poids généré par une "colonne" imaginaire de liquide qui existe au-dessus de lui, de la surface du liquide jusqu'à sa peau et la surface de la mer.
a masse de colonne de liquide ($M$) peut être calculé à partir de a densité du liquide ($\rho_w$) et le volume de la colonne ($V$).
Pour calculer a densité du liquide ($\rho_w$), on utilise l'équation suivante :
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
Et pour le volume de la colonne ($V$), l'équation est la suivante :
| $ V = S h $ |
De cette manière, la valeur de a masse de colonne de liquide ($M$) est obtenue par :
| $ M = \rho_w S h $ |
Ceci est valide tant que a hauteur de la colonne de liquide ($S$) reste constant tout au long de a hauteur de la colonne ($h$).
La section peut changer de forme, mais pas de surface.
ID:(2207, 0)
Force de l'eau sur le bas de la colonne
Concept
Une fois que le volume et donc la masse de la colonne sont connus, la force qu'elle exerce sur sa base peut être calculée. Il est important de noter que cela s'applique aux liquides considérés comme incompressibles, ce qui signifie que les couches inférieures du liquide sont supposées ne pas être compressées par le poids des couches supérieures.
Ce principe peut être appliqué pour calculer la force exercée par n'importe quel liquide, tel que l'eau ou l'huile, et est particulièrement utile en ingénierie hydraulique et en mécanique des fluides.
Étant donné que a masse de colonne de liquide ($M$) dépend de a densité du liquide ($\rho_w$), a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$) selon l'équation :
| $ M = \rho_w S h $ |
et que a force de la colonne ($F$) est représenté par a accélération gravitationnelle ($g$) par :
| $ F = M g $ |
alors l'expression peut être écrite comme suit :
| $ F = S h \rho_w g $ |
.
ID:(2208, 0)
Introduction de la notion de pression
Concept
En mécanique, nous décrivons comment les corps de masse définie se déplacent. Dans le cas d'un liquide, son mouvement n'est pas uniforme, et chaque section du liquide se déplace différemment. Cependant, ces \\"sections\\" n'ont pas une masse définie, car elles ne sont pas des objets définis ou séparés.
Pour résoudre ce problème, nous pouvons segmenter le liquide en une série de petits volumes séparés et, si possible, estimer leur masse en utilisant la densité. De cette manière, nous pouvons introduire l\'idée que les forces définissent le mouvement du liquide.
Cependant, en dernière analyse, les volumes sont arbitraires, et ce qui finit par générer le mouvement est la force agissant sur la face du volume. Par conséquent, il est plus logique d'introduire le concept de force de la colonne ($F$) par un tel hauteur de la colonne de liquide ($S$), appelé A pression de la colonne d'eau ($p$).
ID:(46, 0)
Pression d'eau en bas de colonne
Concept
La a force de la colonne ($F$) agissant sur le fond dépend de a hauteur de la colonne de liquide ($S$) dans le sens où si cette dernière varie, la force variera dans la même proportion. Dans ce sens, a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) ne sont pas interdépendants ; ils varient de manière proportionnelle. Il est logique de définir cette proportion comme a pression ($p$) :
Comme la a force de la colonne ($F$) générée par une colonne de liquide de a hauteur de la colonne ($h$), a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) est
| $ F = S h \rho_w g $ |
et la a pression de la colonne d'eau ($p$) est alors définie comme
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
nous avons donc que la a pression de la colonne d'eau ($p$) générée par une colonne de liquide est
| $ p = \rho_w g h $ |
Ceci est la loi de la pression hydrostatique, également connue sous le nom de loi de Pascal, principalement attribuée à Blaise Pascal [1].
[1] "Traité de l'équilibre des liqueurs", Blaise Pascal, 1663.
ID:(2085, 0)
Somme de la pression de colonne et de l'atmosphère
Concept
Si l'on considère que la colonne est sous l'influence de a pression atmosphèrique ($p_0$), alors la contribution de a pression atmosphèrique ($p_0$) doit être ajoutée à A pression de la colonne d'eau ($p$) de la colonne, comme illustré ici :
Lors du calcul de a pression de la colonne d'eau ($p$) à une certaine profondeur, il est important de prendre en compte que la surface du liquide est exposée à A pression atmosphèrique ($p_0$), ce qui peut affecter la valeur de la pression à cet endroit. Par conséquent, il est nécessaire de généraliser l'équation de a pression de la colonne d'eau ($p$) pour inclure non seulement la colonne de liquide a densité du liquide ($\rho_w$), a hauteur de la colonne ($h$) et a accélération gravitationnelle ($g$), mais également a pression atmosphèrique ($p_0$) :
| $ p_t = p_0 + \rho_w g h $ |
Il n'est pas toujours nécessaire de prendre en compte la pression atmosphérique dans la modélisation :
Dans de nombreux cas, la pression atmosphérique est présente dans tout le système, de sorte que les différences de pression ne dépendent pas d'elle.
ID:(2210, 0)
Indépendance de la forme du conteneur
Concept
Il est important de comprendre que la pression dépend uniquement de la profondeur et qu'il n'est pas nécessaire qu\'une colonne de liquide se trouve directement au-dessus du point où la pression est mesurée. Cela est dû au fait que toute différence de pression à la même profondeur entraînera un flux jusqu\'à ce que la pression soit uniforme.
En d\'autres termes, la pression est une grandeur scalaire qui ne dépend que de la distance verticale de la surface du liquide jusqu\'au point de mesure. Cela est connu sous le nom de pression hydrostatique, qui est un concept fondamental en mécanique des fluides et est utilisé pour comprendre le comportement des fluides dans diverses applications, telles que les systèmes hydrauliques et les conduites.
ID:(932, 0)
Le paradoxe de Pascal
Description
Le paradoxe de Pascal fait référence à une expérience menée par Blaise Pascal, un mathématicien et physicien français du XVIIe siècle. Dans l'expérience, un tube en verre haut a été rempli d\'eau, et un long tube étroit a été inséré à travers un trou dans le haut, permettant à l\'eau d\'être piégée à l\'intérieur du tube. Malgré le fait que le tube soit mince et contienne une petite quantité d\'eau, il a été observé que la pression au fond du tube était égale à la pression au fond du plus grand récipient.
Un exemple de cela est observé dans le soi-disant paradoxe de Pascal, où un pot en verre avec 50 litres d\'eau est brisé en plaçant un tube très fin de seulement 47 mètres contenant seulement un litre d\'eau. Vous pouvez regarder une démonstration de cette expérience dans la vidéo suivante:
ID:(11949, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ F = S h \rho_w g $
F = S * h * rho_w * g
$ F = M g $
F_g = m_g * g
$ M = \rho_w S h $
M = rho_w * S * h
$ p \equiv\displaystyle\frac{ F }{ S }$
p = F / S
$ p = \rho_w g h $
p = rho_w * g * h
$ p_t = p_0 + \rho_w g h $
p_t = p_0 + rho_w * g * h
$ \rho_w = \displaystyle\frac{ M }{ V }$
rho_w = M / V
$ V = S h $
V = S * h
ID:(15433, 0)
Volume de la colonne
Équation
Le volume de la colonne ($V$) est déterminé par a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$) et est calculé comme suit :
| $ V = S h $ |
ID:(931, 0)
Densité d'un liquide
Équation
La a densité du liquide ($\rho_w$) est calculée à partir de a masse de colonne de liquide ($M$) et le volume de la colonne ($V$) en utilisant l'équation :
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
ID:(15091, 0)
Masse de la colonne d'eau
Équation
En utilisant a densité du liquide ($\rho_w$), a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$), vous pouvez calculer a masse de colonne de liquide ($M$) avec la formule :
| $ M = \rho_w S h $ |
A masse de colonne de liquide ($M$) peut être calculé à partir de a densité du liquide ($\rho_w$) et le volume de la colonne ($V$).
Pour calculer a densité du liquide ($\rho_w$), on utilise l'équation suivante :
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
Et pour le volume de la colonne ($V$), l'équation est la suivante :
| $ V = S h $ |
De cette manière, la valeur de a masse de colonne de liquide ($M$) est obtenue par :
| $ M = \rho_w S h $ |
ID:(4340, 0)
Force gravitationnelle
Équation
A force gravitationnelle ($F_g$) est basé sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui reflète l'intensité de la gravité à la surface de la planète. Cette dernière est identifiée par a accélération gravitationnelle ($g$), qui est égal à $9.8 m/s^2$.
Par conséquent, on en conclut que :
| $ F = M g $ |
| $ F_g = m_g g $ |
ID:(3241, 0)
Force de la colonne d'eau
Équation
A force de la colonne ($F$) est calculé à partir de a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$), a hauteur de la colonne ($h$) et a accélération gravitationnelle ($g$) en utilisant :
| $ F = S h \rho_w g $ |
Étant donné que a masse de colonne de liquide ($M$) dépend de a densité du liquide ($\rho_w$), a hauteur de la colonne de liquide ($S$) et a hauteur de la colonne ($h$) selon l'équation :
| $ M = \rho_w S h $ |
et que a force de la colonne ($F$) est représenté par a accélération gravitationnelle ($g$) par :
| $ F = M g $ |
alors l'expression peut être écrite comme suit :
| $ F = S h \rho_w g $ |
.
ID:(4248, 0)
Définition de la pression
Équation
A pression de la colonne d'eau ($p$) se calcule à partir de a force de la colonne ($F$) et a hauteur de la colonne de liquide ($S$) comme suit :
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Pression de colonne
Équation
Si l'on considère l'expression de a force de la colonne ($F$) et qu'on la divise par a hauteur de la colonne de liquide ($S$), on obtient a pression de la colonne d'eau ($p$). Au cours de ce processus, nous simplifions a hauteur de la colonne de liquide ($S$), de sorte qu'il ne dépende plus de lui. L'expression résultante est la suivante :
| $ p = \rho_w g h $ |
Comme la a force de la colonne ($F$) générée par une colonne de liquide de a hauteur de la colonne ($h$), a hauteur de la colonne de liquide ($S$), a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$) est
| $ F = S h \rho_w g $ |
et la a pression de la colonne d'eau ($p$) est alors définie comme
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
nous avons donc que la a pression de la colonne d'eau ($p$) générée par une colonne de liquide est
| $ p = \rho_w g h $ |
ID:(4249, 0)
Pression de colonne avec pression atmosphérique
Équation
A pression de la colonne d'eau ($p$) est avec a densité du liquide ($\rho_w$), a hauteur de la colonne ($h$), a accélération gravitationnelle ($g$) et a pression atmosphèrique ($p_0$) égal à :
| $ p_t = p_0 + \rho_w g h $ |
ID:(4250, 0)