Presión hidrostática
Storyboard 
Una columna de líquido ejerce una fuerza sobre su base debido a su masa. Dado que esta fuerza es directamente proporcional a la área transversal, resulta útil introducir el concepto de fuerza por unidad de área, al cual llamamos presión.
La presión puede verse afectada por el movimiento del líquido, y hacemos una distinción entre la presión general y la presión hidrostática (hidro = líquido, estática = sin movimiento).
ID:(874, 0)
Presión hidrostática
Storyboard 
Una columna de líquido ejerce una fuerza sobre su base debido a su masa. Dado que esta fuerza es directamente proporcional a la área transversal, resulta útil introducir el concepto de fuerza por unidad de área, al cual llamamos presión. La presión puede verse afectada por el movimiento del líquido, y hacemos una distinción entre la presión general y la presión hidrostática (hidro = líquido, estática = sin movimiento).
Variables
Cálculos
Cálculos
Ecuaciones
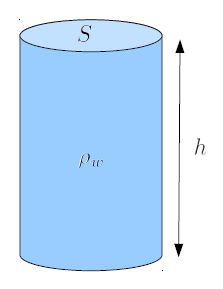
Dado que la masa de la columna de líquido ($M$) depende de la densidad del líquido ($\rho_w$), la sección de la columna ($S$) y la altura de la columna ($h$) de acuerdo con la ecuaci n:
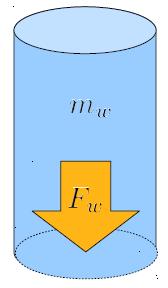
y la fuerza de la columna ($F$) est representada con la aceleración gravitacional ($g$) por:
entonces, la expresi n se puede escribir de la siguiente manera:
Como la la fuerza de la columna ($F$) generada por una columna de liquido de la altura de la columna ($h$), la sección de la columna ($S$), la densidad del líquido ($\rho_w$) y la aceleración gravitacional ($g$) es
y la la presión de la columna de agua ($p$) se define entonces como
se tiene que la la presión de la columna de agua ($p$) generada por una columna de liquido es
La masa de la columna de líquido ($M$) se puede calcular a partir de la densidad del líquido ($\rho_w$) y el volumen de la columna ($V$).
Para calcular la densidad del líquido ($\rho_w$), se utiliza la siguiente ecuaci n:
Y para el volumen de la columna ($V$), se aplica la ecuaci n:
De esta manera, se obtiene el valor de la masa de la columna de líquido ($M$) mediante:
Ejemplos
Para estudiar el comportamiento de los l quidos, es til introducir el concepto de una columna de l quido. Esta columna es una abstracci n de un recipiente cil ndrico (como una probeta) que contiene l quido, y permite estudiar la fuerza a la que un objeto dentro de ella est expuesto.
Una vez que se introduce este concepto, se puede pensar en su existencia independiente del recipiente que la contiene. Por ejemplo, un buzo nadando en alta mar est expuesto al peso que genera una 'columna' imaginaria de l quido que existe sobre l, desde la superficie del l quido hasta su piel y la superficie del mar.
la masa de la columna de líquido ($M$) se puede calcular a partir de la densidad del líquido ($\rho_w$) y el volumen de la columna ($V$).
Para calcular la densidad del líquido ($\rho_w$), se utiliza la siguiente ecuaci n:
Y para el volumen de la columna ($V$), se aplica la ecuaci n:
De esta manera, se obtiene el valor de la masa de la columna de líquido ($M$) mediante:
Esto es v lido siempre y cuando la sección de la columna ($S$) se mantenga constante a lo largo de la altura de la columna ($h$).
La secci n puede cambiar en su forma, pero no en su superficie.
Una vez que se conoce el volumen y, por lo tanto, la masa de la columna de l quido, se puede calcular la fuerza que esta ejerce sobre su base. Es importante tener en cuenta que esto se aplica a l quidos que se consideran incompresibles, lo que significa que se supone que las capas inferiores del l quido no se comprimen debido al peso de las capas superiores.
Este principio se puede aplicar para calcular la fuerza ejercida por cualquier l quido, como agua o aceite, y es particularmente til en ingenier a hidr ulica y mec nica de fluidos.
Dado que la masa de la columna de líquido ($M$) depende de la densidad del líquido ($\rho_w$), la sección de la columna ($S$) y la altura de la columna ($h$) de acuerdo con la ecuaci n:
y la fuerza de la columna ($F$) est representada con la aceleración gravitacional ($g$) por:
entonces, la expresi n se puede escribir de la siguiente manera:
En mec nica, se describe c mo se desplazan los cuerpos con masa definida. En el caso de un l quido, su movimiento no es uniforme, cada sector se desplaza de manera distinta. Sin embargo, estos "sectores" no tienen una masa definida ya que no son objetos definidos ni separados.
Para resolver esta problem tica, se puede segmentar el l quido en una serie de peque os vol menes separados y, si es posible, estimar su masa mediante la densidad. De esta manera, se puede introducir la idea de que existen fuerzas que definen el movimiento del l quido.
Sin embargo, en ltima instancia, los vol menes son arbitrarios y lo que acaba generando el movimiento es la fuerza que act a en la cara del volumen. Por lo tanto, tiene m s sentido introducir el concepto de ERROR:10113,0 por dicha ERROR:6002,0, que se llama la presión de la columna de agua ($p$).
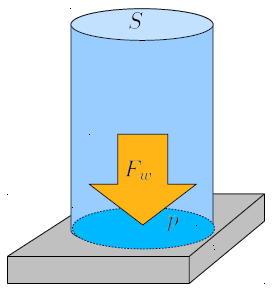
La la fuerza de la columna ($F$) que act a sobre el fondo depende de la sección de la columna ($S$) en el sentido de que si esta ltima var a, la fuerza lo har en la misma proporci n. En este sentido, la fuerza de la columna ($F$) y la sección de la columna ($S$) no est n vinculados de manera dependiente, var an proporcionalmente, por lo que tiene sentido definir esta proporci n como la presión ($p$):
Como la la fuerza de la columna ($F$) generada por una columna de liquido de la altura de la columna ($h$), la sección de la columna ($S$), la densidad del líquido ($\rho_w$) y la aceleración gravitacional ($g$) es
y la la presión de la columna de agua ($p$) se define entonces como
se tiene que la la presión de la columna de agua ($p$) generada por una columna de liquido es
Esta es la ley de presi n hidrost tica, tambi n conocida como ley de Pascal, atribuida principalmente a Blaise Pascal [1].
![]() [1] "Trait de l' quilibre des liqueurs" (Tratado sobre el equilibrio de los l quidos), Blaise Pascal, 1663.
[1] "Trait de l' quilibre des liqueurs" (Tratado sobre el equilibrio de los l quidos), Blaise Pascal, 1663.
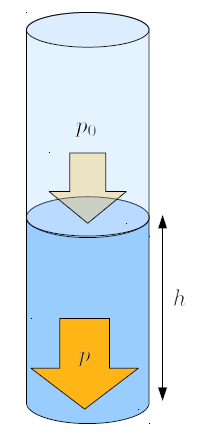
Si se considera que la columna est bajo la influencia de la presión atmosférica ($p_0$), entonces se debe sumar a la presión de la columna de agua ($p$) de la columna la contribuci n de esta:
Cuando calculamos la presión de la columna de agua ($p$) a cierta profundidad, es fundamental tener en cuenta que la superficie del l quido est expuesta a la presión atmosférica ($p_0$), lo que puede afectar el valor de la presi n en ese punto. Por lo tanto, es necesario generalizar la ecuaci n de la presión de la columna de agua ($p$) para que incluya no solo la columna de l quido la densidad del líquido ($\rho_w$), la altura de la columna ($h$), y la aceleración gravitacional ($g$), sino tambi n la presión atmosférica ($p_0$):
No siempre es necesario tener en cuenta la presi n atmosf rica en la modelaci n:
En muchos casos, la presi n atmosf rica est presente en todo el sistema, por lo que las diferencias de presi n no dependen de ella.
Es importante comprender que la presi n depende nicamente de la profundidad y no es necesario que exista una columna de l quido directamente encima del punto en que se mide la presi n. Esto se debe a que cualquier diferencia de presi n a la misma profundidad provocar un flujo hasta que la presi n sea uniforme.
En otras palabras, la presi n es una magnitud escalar que solo depende de la distancia vertical desde la superficie del l quido hasta el punto de medici n. Esto se conoce como presi n hidrost tica, que es un concepto fundamental en la mec nica de fluidos y se utiliza para comprender el comportamiento de los fluidos en diversas aplicaciones, como en sistemas hidr ulicos y tuber as.
La paradoja de Pascal se refiere a un experimento realizado por Blaise Pascal, un matem tico y f sico franc s del siglo XVII. En el experimento, se llen un tubo de vidrio alto con agua y se insert un tubo largo y estrecho a trav s de un agujero en la parte superior, lo que permiti que el agua quedara atrapada dentro del tubo. A pesar de que el tubo era delgado y ten a una peque a cantidad de agua, se observ que la presi n en la parte inferior del tubo era igual a la presi n en la parte inferior del recipiente m s grande.
Un ejemplo de esto se ve en la llamada paradoja de Pascal, en la que una jarra de vidrio con 50 litros de agua explota al colocar un tubito muy delgado de solo 47 metros que contiene solo un litro de agua. Puede ver una demostraci n de este experimento en el siguiente video:
El volumen de la columna ($V$) se determina a partir de la sección de la columna ($S$) y la altura de la columna ($h$) y su c lculo se realiza mediante:
La la densidad del líquido ($\rho_w$) se calcula a partir de la masa de la columna de líquido ($M$) y el volumen de la columna ($V$) utilizando la ecuaci n:
Utilizando la densidad del líquido ($\rho_w$), la sección de la columna ($S$), y la altura de la columna ($h$), se puede calcular la masa de la columna de líquido ($M$) mediante la f rmula:
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta ltima es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
La fuerza de la columna ($F$) se calcula de la sección de la columna ($S$), la densidad del líquido ($\rho_w$), la altura de la columna ($h$) y la aceleración gravitacional ($g$) mediante:
La presión de la columna de agua ($p$) se calcula a partir de la fuerza de la columna ($F$) y la sección de la columna ($S$) de la siguiente manera:
Si consideramos la expresi n de la fuerza de la columna ($F$) y la dividimos por la sección de la columna ($S$), obtenemos la presión de la columna de agua ($p$). Durante este proceso, simplificamos la sección de la columna ($S$), por lo que ya no depende de esta. La expresi n resultante es la siguiente:
La presión de la columna de agua ($p$) es con la densidad del líquido ($\rho_w$), la altura de la columna ($h$), la aceleración gravitacional ($g$) y la presión atmosférica ($p_0$) igual a:
ID:(874, 0)