Hydrostatic pressure
Storyboard 
A column of liquid exerts force on its base due to its mass. Since this force is directly proportional to the cross-sectional area, it is useful to introduce the concept of force per unit area, which we call pressure.
Pressure can be influenced by the motion of the liquid, and we distinguish between general pressure and hydrostatic pressure (hydro = liquid, static = without motion).
ID:(874, 0)
Hydrostatic pressure
Storyboard 
A column of liquid exerts force on its base due to its mass. Since this force is directly proportional to the cross-sectional area, it is useful to introduce the concept of force per unit area, which we call pressure. Pressure can be influenced by the motion of the liquid, and we distinguish between general pressure and hydrostatic pressure (hydro = liquid, static = without motion).
Variables
Calculations
Calculations
Equations
Since the mass of liquid column ($M$) depends on the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$) according to the equation:
and the column force ($F$) is represented with the gravitational Acceleration ($g$) by:
the expression can be written as follows:
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
and the the water column pressure ($p$) is then defined as
we have that the the water column pressure ($p$) generated by a column of liquid is
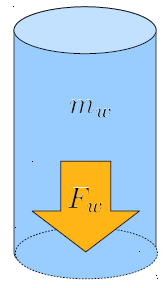
The mass of liquid column ($M$) can be calculated from the liquid density ($\rho_w$) and the column volume ($V$).
To calculate the liquid density ($\rho_w$), the following equation is used:
And for the column volume ($V$), the equation is:
This way, the value of the mass of liquid column ($M$) is obtained by:
Examples
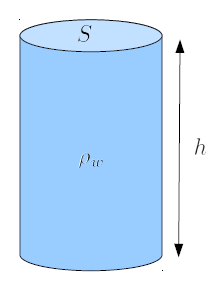
To study the behavior of liquids, it is useful to introduce the concept of a column of liquid. This column is an abstraction of a cylindrical container (such as a graduated cylinder) containing liquid, and allows us to study the force to which an object inside it is exposed.
Once this concept is introduced, we can think of its existence independently of the container that contains it. For example, a diver swimming in open sea is exposed to the weight generated by an 'imaginary' column of liquid that exists above them, from the surface of the liquid to their skin and the surface of the sea.
the mass of liquid column ($M$) can be calculated from the liquid density ($\rho_w$) and the column volume ($V$).
To calculate the liquid density ($\rho_w$), the following equation is used:
And for the column volume ($V$), the equation is:
This way, the value of the mass of liquid column ($M$) is obtained by:
This is valid as long as the column Section ($S$) remains constant throughout the column height ($h$).
The section may change in its shape, but not in its surface.
Once the volume and thus the mass of the column is known, the force it exerts on its bottom can be calculated. It is important to note that this applies to liquids that are considered incompressible, which means that the lower layers of the liquid are assumed not to be compressed by the weight of the layers above them.
This principle can be applied to calculate the force exerted by any liquid, such as water or oil, and is particularly useful in hydraulic engineering and fluid mechanics.
Since the mass of liquid column ($M$) depends on the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$) according to the equation:
and the column force ($F$) is represented with the gravitational Acceleration ($g$) by:
the expression can be written as follows:
In mechanics, we describe how bodies with defined mass move. In the case of a liquid, its movement is not uniform, and each section of the liquid moves differently. However, these \\"sections\\" do not have a defined mass, as they are not defined or separate objects.
To address this issue, we can segment the liquid into a series of small, separated volumes and, if possible, estimate their mass using density. In this way, we can introduce the idea that forces define the movement of the liquid.
However, ultimately volumes are arbitrary, and what ultimately generates the movement is the force acting on the volume's face. Therefore, it makes more sense to introduce the concept of ERROR:10113,0 per such ERROR:6002,0, which is called the water column pressure ($p$).
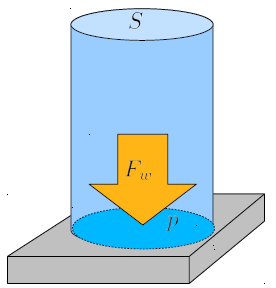
The the column force ($F$) acting on the bottom depends on the column Section ($S$) in the sense that if the latter varies, the force will vary in the same proportion. In this sense, the column force ($F$) and the column Section ($S$) are not interdependent; they vary proportionally. It makes sense to define this proportion as the pressure ($p$):
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
and the the water column pressure ($p$) is then defined as
we have that the the water column pressure ($p$) generated by a column of liquid is
This is the law of hydrostatic pressure, also known as Pascal's Law, primarily attributed to Blaise Pascal [1].
![]() [1] "Trait de l' quilibre des liqueurs" (Treatise on the Equilibrium of Liquids), Blaise Pascal, 1663.
[1] "Trait de l' quilibre des liqueurs" (Treatise on the Equilibrium of Liquids), Blaise Pascal, 1663.
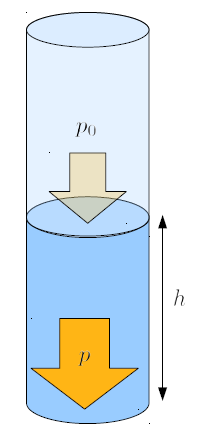
If it is considered that the column is influenced by the atmospheric pressure ($p_0$), then the contribution of the atmospheric pressure ($p_0$) must be added to the water column pressure ($p$) of the column, as shown here:
When calculating the water column pressure ($p$) at a certain depth, it's important to consider that the liquid's surface is exposed to the atmospheric pressure ($p_0$), which can affect the pressure value at that point. Therefore, it's necessary to generalize the equation for the water column pressure ($p$) to include not only the liquid column the liquid density ($\rho_w$), the column height ($h$), and the gravitational Acceleration ($g$) but also the atmospheric pressure ($p_0$):
It is not always necessary to consider atmospheric pressure in the modeling:
In many cases, atmospheric pressure is present throughout the system, so pressure differences do not depend on it.
It is important to understand that pressure depends solely on depth and it is not necessary for a column of liquid to be directly above the point where pressure is being measured. This is because any pressure difference at the same depth will lead to a flow until the pressure becomes uniform.
In other words, pressure is a scalar quantity that only depends on the vertical distance from the surface of the liquid to the point of measurement. This is known as hydrostatic pressure, which is a fundamental concept in fluid mechanics and is used to understand the behavior of fluids in various applications, such as in hydraulic systems and pipelines.
The Pascal's paradox refers to an experiment conducted by Blaise Pascal, a French mathematician and physicist, in the 17th century. In the experiment, a tall glass tube was filled with water, and a long narrow tube was inserted through a hole in the top, allowing the water to be trapped inside the tube. Despite the tube being thin and having a small amount of water, it was observed that the pressure at the bottom of the tube was equal to the pressure at the bottom of the larger container.
An example of this is seen in the so-called Pascal's paradox, where a glass jar with 50 liters of water is shattered by placing a very thin tube of only 47 meters containing only one liter of water. You can watch a demonstration of this experiment in the following video:
The column volume ($V$) is determined by the column Section ($S$) and the column height ($h$), and it is calculated as follows:
The the liquid density ($\rho_w$) is calculated from the mass of liquid column ($M$) and the column volume ($V$) using the equation:
Using the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$), you can calculate the mass of liquid column ($M$) with the formula:
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
The column force ($F$) is calculated from the column Section ($S$), the liquid density ($\rho_w$), the column height ($h$) and the gravitational Acceleration ($g$) using:
The water column pressure ($p$) is calculated from the column force ($F$) and the column Section ($S$) as follows:
If we consider the expression of the column force ($F$) and divide it by the column Section ($S$), we obtain the water column pressure ($p$). In this process, we simplify the column Section ($S$), so it no longer depends on it. The resulting expression is:
The water column pressure ($p$) is with the liquid density ($\rho_w$), the column height ($h$), the gravitational Acceleration ($g$) and the atmospheric pressure ($p_0$) equal to:
ID:(874, 0)